Download Gauss`s Law and Conductors Powerpoint

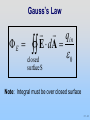
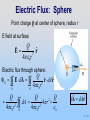
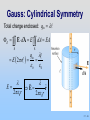
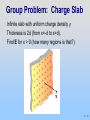
Workshop: Using Visualization
in Teaching Introductory E&M
AAPT National Summer Meeting, Edmonton, Alberta,
Canada.
Organizers: John Belcher, Peter Dourmashkin,
Carolann Koleci, Sahana Murthy
P07 - 1
MIT Class:
Gauss’s Law, Conductors and
Capacitors, Shielding
P07 - 2
Gauss’s Law
The first Maxwell Equation
A very useful computational technique
This is important!
P07 - 3
Gauss’s Law – The Idea
The total “flux” of field lines penetrating any of
these surfaces is the same and depends only
on the amount of charge inside
P07 - 4
Gauss’s Law – The Equation
  qin
F E   E  dA 
closed
surface S
0
Electric flux FE (the surface integral of E over
closed surface S) is proportional to charge
inside the volume enclosed by S
P07 - 5
Now the Details
P07 - 6
Electric Flux FE
Case I: E is constant vector field
perpendicular to planar surface S of area A
 
F E   E  dA
F E   EA
Our Goal: Always reduce
problem to this
P07 - 7
Electric Flux FE
Case II: E is constant vector field directed
at angle q to planar surface S of area A
n̂
 
F E   E  dA
dA  dA nˆ
F E  EA cosq
P07 - 8
PRS Question:
Flux Thru Sheet
P07 - 9
PRS: Flux
15
The flux through the planar surface below
(positive unit normal to left):
+q
0%
0%
0%
0%
1.
2.
3.
4.
n̂
is positive.
is negative.
is zero.
I don’t know
-q
P07 -10
PRS Answer: Flux
Answer: 2. The flux is negative.
+q
n̂
E
-q
The field lines go from left to right,
opposite the assigned normal direction.
Hence the flux is negative.
P07 - 11
Gauss’s Law
  qin
F E   E  dA 
closed
surface S
0
Note: Integral must be over closed surface
P07 -12
Open and Closed Surfaces
A rectangle is an open surface — it does NOT contain a volume
A sphere is a closed surface — it DOES contain a volume
P07 -13
Area Element dA: Closed Surface
For closed surface, dA is normal to surface
and points outward
( from inside to outside)
FE > 0 if E points out
FE < 0 if E points in
P07 -14
Electric Flux FE
Case III: E not constant, surface curved
dA
S
E
d FE  E  d A
F E   dF E
In practice you’ll never do an integral,
although here’s an example of non-constant E
P07 -15
PRS Question:
Flux Thru Sphere
P07 -16
PRS: Flux thru Sphere
15
The total flux through the below spherical
surface is
+q
0%
0%
0%
0%
1.
2.
3.
4.
positive (net outward flux)
negative (net inward flux)
zero.
I don’t know
P07 -17
PRS Answer: Flux thru Sphere
Answer: 3. The total flux is zero
+
q
We know this from Gauss’s Law:
qin
F E   E  dA 
0
closed
surface S
No enclosed charge  no net flux.
Flux in on left cancelled by flux out on right
P07 -18
Electric Flux: Sphere
Point charge Q at center of sphere, radius r
E field at surface:
E
Q
4 0 r
2
rˆ
Electric flux through sphere:
FE 
Q
 E  dA   4 r
S

4 0 r
2
 dA
S

rˆ  dA rˆ
0
S
Q
2
Q
4 0 r
4 r 
2
2
Q
0

dA  dA rˆ
P07 -19
Arbitrary Gaussian Surfaces
  Q
F E   E  dA 
closed
surface S
0
True for all surfaces such as S1, S2 or S3
Why? As A gets bigger E gets smaller
P07 -20
Choosing Gaussian Surface
  Q
F E   E  dA 
0
closed
surface S
True for ALL surfaces
Useful (to calculate E)
for SOME surfaces
Desired E: Punch through surface & be constant.
Flux is EA or -EA.
Other E: Run along surface.
Flux is zero
P07 -21
Symmetry & Gaussian Surfaces
Desired E: Punch through surface & be constant
So Gauss’s Law good to calculate E field from
highly symmetric sources
Symmetry
Gaussian Surface
Spherical
Concentric Sphere
Cylindrical
Coaxial Cylinder
Planar
Gaussian “Pillbox”
P07 -22
Applying Gauss’s Law
1. Identify regions in which to calculate E field.
2. Choose Gaussian surfaces S: Symmetry
 
3. Calculate F E   E  dA
S
4. Calculate qin, charge enclosed by surface S
5. Apply Gauss’s Law to calculate E:
  qin
F E   E  dA 
closed
surface S
0
P07 -23
Examples:
Spherical Symmetry
Cylindrical Symmetry
Planar Symmetry
P07 -24
Gauss: Spherical Symmetry
+Q uniformly distributed throughout non-conducting
solid sphere of radius a. Find E everywhere
P07 -25
Gauss: Spherical Symmetry
Symmetry is Spherical

E  E rˆ
Use Gaussian Spheres
P07 -26
Gauss: Spherical Symmetry
Region 1: r > a
Draw Gaussian Sphere in Region 1 (r > a)
Note: r is arbitrary
but is the radius for
which you will
calculate the E field!
P07 -27
Gauss: Spherical Symmetry
Region 1: r > a
Total charge enclosed qin = +Q
FE 
 E  dA  E  dA  EA
S

 E 4 r
2

F E  4 r E 
2
E
Q
4 0 r
2
S
qin
0

E
Q
0
Q
4 0 r
2
rˆ
P07 -28
Gauss: Spherical Symmetry
Region 2: r < a
Total charge enclosed:
4 3
3
 r 


r
3
Q   3 Q
qin  
 4 a 3 
a 


3

OR qin  V
Gauss’s law:
3

qin
r Q
2
F E  E  4 r  
 3 
0  a  0
Q r
Q r
E
E
rˆ
3
3
4 0 a
4 0 a
P07 -29
PRS Question:
Field Inside Spherical Shell
P07 -30
PRS: Spherical Shell
We just saw that in a solid sphere
of charge the electric field grows
linearly with distance. Inside the
charged spherical shell at left (r<a)
what does the electric field do?
0%
0%
0%
0%
0%
1.
2.
3.
4.
5.
:15
a
Q
Constant and Zero
Constant but Non-Zero
Still grows linearly
Some other functional form (use Gauss’ Law)
Can’t determine with Gauss Law
P07 -31
PRS Answer: Spherical Shell
Answer: 1. Constant and Zero
Q
a
Spherical symmetry
 Use Gauss’ Law with spherical surface.
Any surface inside shell contains no charge
 No flux
E = 0!
P07 -32
Demonstration
Field Inside Spherical Shell
(Grass Seeds):
P07 -33
Gauss: Cylindrical Symmetry
Infinitely long rod with uniform charge density l
Find E outside the rod.
P07 -34
Gauss: Cylindrical Symmetry
Symmetry is Cylindrical

E  E rˆ
Use Gaussian Cylinder
Note: r is arbitrary but is
the radius for which you
will calculate the E field!
 is arbitrary and should
divide out
P07 -35
Gauss: Cylindrical Symmetry
Total charge enclosed: qin  l
FE 
 E  dA  E  dA  EA
S
S
l
 E  2 r  

0 0
qin
l
l
E
E
rˆ
2 0 r
2 0 r
P07 -36
Gauss: Planar Symmetry
Infinite slab with uniform charge density s
Find E outside the plane
P07 -37
Gauss: Planar Symmetry
Symmetry is Planar

E   E xˆ
Use Gaussian Pillbox
x̂
Note: A is arbitrary (its
size and shape) and
should divide out
Gaussian
Pillbox
P07 -38
Gauss: Planar Symmetry
Total charge enclosed: qin  sA
NOTE: No flux through side of cylinder, only endcaps
FE 
 E  dA  E  dA  EAEndcaps
S
S
sA
 E  2 A 

0
0
qin

s
s xˆ to right
E
E
2 0
2 0 -xˆ to left

E
+
+
+
+
+
+
+
+
+
+
+
+
x
A
E
s
P07 -39
PRS Question:
Slab of Charge
P07 -40
PRS: Slab of Charge
15
A positively charged, semi-infinite (in x & y) flat slab
has thickness 2d.
z-axis is perp. to the sheet, with center at z = 0.
z
2d

z=0
At the plane’s center (z = 0), E
0%
0%
0%
0%
1.
2.
3.
4.
points in the positive z-direction
points in the negative z-direction
is zero
I don’t know
P07 -41
PRS Answer: Slab of Charge
Answer: 3. E(z=0) is zero
z
2d

z=0
Symmetry tell us this – the amount of charge
above and below the center of the plane is equal
hence the fields cancel.
Another way of thinking about this:
Since you can’t tell which way the field would
point it must be 0.
P07 -42
Group Problem: Charge Slab
Infinite slab with uniform charge density 
Thickness is 2d (from x=-d to x=d).
Find E for x > 0 (how many regions is that?)
x̂
P07 -43
Potential from E
P07 -44
Potential for Uniformly Charged
Non-Conducting Solid Sphere
From Gauss’s Law
 Q ˆ
 4 r 2 r, r  R

0
E
 Qr rˆ , r  R
 4 0 R 3
B
Use
VB  VA    E  d s
A
Region 1: r > a
Point Charge!
VB  V      
r

0
Q
1
Q
dr 
2
4 0 r
4 0 r
P07 -45
Potential for Uniformly Charged
Non-Conducting Solid Sphere
Region 2: r < a
R
r
VD  V      drE  r  R   R drE  r  R 
0
R
Q
Qr
   dr
  dr
2

R
4 0 r
4 0 R3
1
r

Q
1 Q 1 2
2


r

R
4 0 R 4 0 R 3 2

1 Q
r2 

 3 2 
8 0 R 
R 
P07 -46
Potential for Uniformly Charged
Non-Conducting Solid Sphere
P07 -47
Group Problem: Charge Slab
Infinite slab with uniform charge density 
Thickness is 2d (from x=-d to x=d).
If V=0 at x=0 (definition) then what is V(x) for x>0?
x̂
P07 -48
Conductors
P07 -49
Conductors and Insulators
Conductor: Charges are free to move
Electrons weakly bound to atoms
Example: metals
Insulator: Charges are NOT free to move
Electrons strongly bound to atoms
Examples: plastic, paper, wood
P07 -50
Conductors
Conductors have free charges
 E must be zero inside the conductor
 Conductors are equipotential objects
E
-
Neutral
Conductor
+
+
+
+
P07 -51
Conductors in Equilibrium
Conductors are equipotential objects:
1) E = 0 inside
2) E perpendicular to surface
3) Net charge inside is 0
P07 -52
Conductors in Equilibrium:
Free Charges Move To Surface
Put net charge inside conductor
It moves to get away from other charges
Java applet link
P07 -53
Conductors in Equilibrium
Conductors are equipotential objects:
1) E = 0 inside
2) E perpendicular to surface
3) Net charge inside is 0
4) Excess charge on surface
E s
0
P07 -54
Start Charging
Capacitors and Capacitance
Our first of 3 standard electronics devices
(Capacitors, Resistors & Inductors)
P07 -55
Capacitors: Store Electric Charge
Capacitor: Two isolated conductors
Equal and opposite charges ±Q
Potential difference DV between them.
Q
C
DV
Units: Coulombs/Volt or
Farads
C is Always Positive
P07 -56
Parallel Plate Capacitor
E 0
E ?
d
E 0
Q  s A
P07 -57
Parallel Plate Capacitor
Oppositely charged plates:
Charges move to inner surfaces to get close
Link to Capacitor Applet
P07 -58
Calculating E (Gauss’s Law)
qin
 E  dA  
S
0
s AGauss
E  AGauss  
0
s
Q
E 
 0 A 0
Note: We only “consider” a single sheet!
Doesn’t the other sheet matter?
P07 -59
Alternate Calculation Method
Top Sheet:
s
E
2 0
++++++++++++++
s
E
2 0
Bottom Sheet:
s
E
2 0
- - - - - - - -- - - - - s
E
2 0
s
s
s
Q
E

 
2 0 2 0  0 A 0
P07 -60
Parallel Plate Capacitor
top
Q
d
DV    E  dS  Ed 
A 0
bottom
0 A
Q
C

DV
d
C depends only on geometric factors A and d
P07 -61
Demonstration:
Big Capacitor
P07 -62
Group Problem: Spherical Shells
These two spherical
shells have equal
but opposite charge.
Find E everywhere
Find V everywhere
(assume V() = 0)
P07 -63
Spherical Capacitor
Two concentric spherical shells of radii a and b
What is E?
Gauss’s Law  E ≠ 0 only for a < r < b,
where it looks like a point charge:

E
Q
40 r
ˆ
r
2
P07 -64
Spherical Capacitor
Qrˆ
DV    E  dS  
 dr rˆ
2
4 0 r
inside
a
outside
b
Q 1 1

  
4 0  b a 
Is this positive or negative? Why?
40
Q
C
 1 1
DV
a b


For an isolated spherical conductor of radius a:
C  40 a
P07 -65
Capacitance of Earth
For an isolated spherical conductor of radius a:
C  40 a
 0  8.85 10
12
Fm
a  6.4 10 m
6
4
C  7 10 F  0.7mF
A Farad is REALLY BIG! We usually use pF (10-12) or nF (10-9)
P07 -66
PRS Questions:
Changing C Dimensions
P07 -67
PRS: Changing Dimensions
:20
A parallel-plate capacitor has plates with equal and
opposite charges ±Q, separated by a distance d, and
is not connected to a battery. The plates are pulled
apart to a distance D > d. What happens?
0%
0%
0%
0%
0%
0%
0%
0%
0%
1.
2.
3.
4.
5.
6.
7.
8.
9.
V increases, Q increases
V decreases, Q increases
V is the same, Q increases
V increases,Q is the same
V decreases, Q is thesame
V is the same, Q is the same
V increases, Q decreases
V decreases, Q decreases
V is the same,Q decreases
P07 -68
PRS Answer: Changing Dimensions
Answer: 4. V increases, Q is the same
With no battery connected to the plates the
charge on them has no possibility of
changing.
In this situation, the electric field doesn’t
change when you change the distance
between the plates, so:
V=Ed
As d increases, V increases.
P07 -69
20 PRS: Changing Dimensions
A parallel-plate capacitor has plates with equal and
opposite charges ±Q, separated by a distance d, and
is connected to a battery. The plates are pulled apart
to a distance D > d. What happens?
1.
2.
3.
4.
5.
6.
7.
8.
9.
V increases, Q increases
V decreases, Q increases
V is the same, Q increases
V increases, Q is the same
V decreases, Q is the same
V is the same, Q is the same
V increases,
Q decreases
V decreases, Q decreases
V is the same, Q decreases
P07 -70
PRS Answer: Changing Dimensions
Answer: 9. V is the same, Q decreases
With a battery connected to the plates the
potential V between them is held constant
In this situation, since
V=Ed
As d increases, E must decrease.
Since the electric field is proportional to the
charge on the plates, Q must decrease as
well.
P07 -71
Demonstration:
Changing C Dimensions
P07 -72
Energy Stored in Capacitor
P07 -73
Energy To Charge Capacitor
+q
-q
1. Capacitor starts uncharged.
2. Carry +dq from bottom to top.
Now top has charge q = +dq, bottom -dq
3. Repeat
4. Finish when top has charge q = +Q, bottom -Q
P07 -74
Work Done Charging Capacitor
At some point top plate has +q, bottom has –q
Potential difference is DV = q / C
Work done lifting another dq is dW = dq DV
+q
-q
P07 -75
Work Done Charging Capacitor
So work done to move dq is:
q 1
dW  dq DV  dq  q dq
C C
Total energy to charge to q = Q:
Q
1
W   dW   q dq
C0
+q
2
1Q

C 2
-q
P07 -76
Energy Stored in Capacitor
Q
Since C 
DV
2
Q
1
1
U
 Q DV  C DV
2C 2
2
2
Where is the energy stored???
P07 -77
Energy Stored in Capacitor
Energy stored in the E field!
Parallel-plate capacitor:
1
U  CV 2
2
1 o A

2 d
 Ed 
2

C
o E 2
2
o A
d
and V  Ed
 ( Ad )  uE  (volume)
uE  E field energy density 
o E
2
2
P07 -78
PRS Question:
Changing C Dimensions
Energy Stored
P07 -79
PRS: Changing Dimensions
A parallel-plate capacitor, disconnected from a
battery, has plates with equal and opposite
20
charges, separated by a distance d.
Suppose the plates are pulled apart until separated
by a distance D > d.
How does the final electrostatic energy stored in
the capacitor compare to the initial energy?
0%
0%
0%
1. The final stored energy is smaller
2. The final stored energy is larger
3. Stored energy does not change.
P07 -80
PRS Answer: Changing Dimensions
Answer: 2. The stored energy increases
As you pull apart the capacitor plates you
increase the amount of space in which the E
field is non-zero and hence increase the
stored energy. Where does the extra energy
come from? From the work you do pulling
the plates apart.
P07 -81
Conductors as Shields
P07 -82
PRS Question:
Point Charge Inside Conductor
P07 -83
PRS: Point Charge in Conductor
A point charge +Q is placed
inside a neutral, hollow,
spherical conductor. As the
charge is moved around
+Q
inside, the electric field
outside
0%
1. is zero and does not change
0%
2. is non-zero but does not change
0%
3. is zero when centered but changes
0%
4. is non-zero and changes
15
0%
5. I don’t know
P07 -84
PRS Answer: Q in Conductor
Answer: 2. is non-zero but
does not change
E = 0 in conductor  -Q on inner surface
Charge conserved  +Q on outer surface
E = 0 in conductor  No “communication”
between –Q & +Q  + Q uniformly distributed
P07 -85
Hollow Conductors
Charge placed INSIDE induces
balancing charge ON INSIDE
+
- - +
+ - +
+q
+ -- - - +
+
+
P07 -86
Hollow Conductors
Charge placed OUTSIDE induces
charge separation ON OUTSIDE
+q
-
-
+
E=0
+
+
P07 -87
PRS Questions:
Point Charge
Inside Conductor
P07 -88
PRS Setup
O2
I2
O1
I1
What happens if we
put Q in the center of
these nested
(concentric) spherical
conductors?
P07 -89
15
PRS: Hollow Conductors
A point charge +Q is placed
at the center of the
conductors. The induced
charges are:
0%
0%
0%
0%
1.
2.
3.
4.
O2
I2
O1
I1
Q(I1) = Q(I2) = -Q; Q(O1) = Q(O2)= +Q
Q(I1) = Q(I2) = +Q; Q(O1) = Q(O2)= -Q
Q(I1) = -Q; Q(O1) = +Q; Q(I2) = Q(O2)= 0
Q(I1) = -Q; Q(O2)= +Q; Q(O1) = Q(I2)= 0
P07 -90
PRS Answer: Hollow Conductors
Answer: 1. The inner faces
are negative, the outer faces
are positive.
O2
I2
O1
I1
Looking in from each conductor, the total
charge must be zero (this gives the inner
surfaces as –Q). But the conductors must
remain neutral (which makes the outer surfaces
have induced charge +Q).
P07 -91
PRS: Hollow Conductors
A point charge +Q is placed
at the center of the
conductors. The potential at
O1 is:
O2
I2
O1
I1
15
0%
0%
0%
1. Higher than at I1
2. Lower than at I1
3. The same as at I1
P07 -92
PRS Answer: Hollow Conductors
Answer: 3. O1 and I1 are at
the same potential
O2
I2
O1
I1
A conductor is an equipotential surface. O1
and I1 are on the same conductor, hence at the
same potential
P07 -93
PRS: Hollow Conductors
A point charge +Q is placed
at the center of the
conductors. The potential at
O2 is:
0%
0%
0%
O2
I2
O1
I1
15
1. Higher than at I1
2. Lower than at I1
3. The same as at I1
P07 -94
PRS Answer: Hollow Conductors
Answer: 2. O2 is lower than I1
O2
I2
V
O1
I1
r
As you move away from the positive point
charge at the center, the potential decreases.
P07 -95
PRS: Hollow Conductors
A point charge +Q is placed
at the center of the
conductors. If a wire is used
to connect the two
conductors, then current
(positive charge) will flow
0%
0%
0%
15
O2
I2
O1
I1
1. from the inner to the outer conductor
2. from the outer to the inner conductor
3. not at all
P07 -96
PRS Answer: Hollow Conductors
Answer: 1. Current flows outward
O2
I2
O1
I1
Positive charges always flow “downhill” – from
high to low potential. Since the inner conductor
is at a higher potential the charges will flow from
the inner to the outer conductor.
P07 -97
PRS: Hollow Conductors
O2
You connect the “charge
I2
sensor’s” red lead to the inner
O1
conductor and black lead to
I1
the outer conductor. What
does it actually measure?
15
1. Charge on I1
0%
2. Charge on O1
0%
0%
3. Charge on I2
0%
4. Charge on O2
0%
5. Charge on O1 – Charge on I2
0%
6. Average charge on inner – ave. on outer
0%
7. Potential difference between outer & inner
0%
8. I don’t know
P07 -98
PRS Answer: Hollow Conductors
Answer: 7. “Charge Sensor”
measures potential difference
between outer & inner conductor
O2
I2
O1
I1
So what is the “charge axis?” From the
capacitance and potential difference it can
calculate Q = CDV which is charge on O1 and
negative charge on I2
P07 -99
Demonstration:
Conductive Shielding
P07100
-
Visualization:
Inductive Charging
P07101
-
Experiment 2:
Faraday Ice Pail
P07102
-
Last Time:
Capacitors
P07103
-
Capacitors: Store Electric Energy
Q
C
DV
To calculate:
1) Put on arbitrary ±Q
2) Calculate E
3) Calculate DV
Parallel Plate Capacitor:
C
0 A
d
P07104
-
Capacitors in Series & Parallel
 In series, V adds:
1
1
1
 
Ceq C1 C2
In parallel, Q adds: 
Ceq  C1  C2
P07105
-
Demonstration:
Dissectible Capacitor
P07106
-
Flow of Charge
New Topics: Current, Current Density,
Resistance, Ohm’s Law
P07107
-
Current: Flow Of Charge
Average current Iav: Charge DQ
flowing across area A in time Dt
DQ
I av 
Dt
Instantaneous current:
differential limit of Iav
dQ
I
dt
Units of Current: Coulomb/second = Ampere
P07108
-
How Big is an Ampere?
•
•
•
•
Household Electronics ~1 A
Battery Powered
~100 mA (1-10 A-Hr)
Household Service
100 A
Lightning Bolt
10 to 100 kA
• To hurt you
• To throw you
• To kill you
40 (5) mA DC(AC)
60 (15) mA DC(AC)
0.5 (0.1) A DC(AC)
• Fuse/Circuit Breaker
15-30 A
P07109
-
Direction of The Current
Direction of current is direction of flow of pos. charge
or, opposite direction of flow of negative charge
P07110
-
Current Density J
J: current/unit area
 I
J  Iˆ
A
Î points in direction of current
I   J  nˆ dA   J  d A
S
S
P07111
-
PRS Question:
Current Density
P07112
-
PRS: Current Density
:15
A current I = 200 mA flows in the above wire. What is
the magnitude of the current density J?
5
cm
0%
0%
0%
0%
0%
0%
0%
1.
2.
3.
4.
5.
6.
7.
J = 40 mA/cm
J = 20 mA/cm
J = 10 mA/cm
J = 1 mA/cm2
J = 2 mA/cm2
J = 4 mA/cm2
I don’t know
20 cm
10
cm
P07113
-
PRS Answer: Current Density
Answer: 6. J = 4 mA/cm2
5 cm
10 cm
20 cm
The area that matters is the cross-sectional
area that the current is punching through –
the 50 cm2 area shaded grey.
So:
J = I/A = 200 mA/50 cm2 = 4 mA/cm2
P07114
-
Why Does Current Flow?
If an electric field is set up in a conductor, charge
will move (making a current in direction of E)
Note that when current is flowing, the conductor is
not an equipotential surface (and Einside ≠ 0)!
P07115
-
Microscopic Picture
Drift speed is velocity forced by applied electric field
in the presence of collisions.
It is typically 4x10-5 m/sec, or 0.04 mm/second!
To go one meter at this speed takes about 10 hours!
How Can This Be?
P07116
-
Conductivity and Resistivity
Ability of current to
flow depends on
density of charges &
rate of scattering
Two quantities summarize this:
s: conductivity
: resistivity
P07117
-
Microscopic Ohm’s Law
E  J

or
J sE
1
s
 and s depend only on the microscopic properties
of the material, not on its shape
P07118
-
Demonstrations:
Water
Temperature Effects on 
P07119
-
PRS Question:
Resistance?
P07120
-
PRS: Resistance
When a current flows in a wire of length L and cross
sectional area A, the resistance of the wire is
15
20%
1.
2.
3.
20%
4. Inversely proportional to both L and A
5. Do Not Know
20%
Proportional to A; inversely proportional to L.
Proportional to both A and L.
Proportional to L; inversely proportional to A.
P07121
-
PRS Answer: Resistance
3. Proportional to L; inversely proportional to A.
The longer the wire the higher the resistance.
The bigger the cross-sectional area of the wire,
the more ways that current can flow through it,
so the lower the resistance.
So, if resistivity is , then
R
L
A
P07122
-
Why Does Current Flow?
Instead of thinking of Electric Field, think of potential
difference across the conductor
P07123
-
Ohm’s Law
What is relationship between DV and current?
b
DV  Vb  Va   E  d s  E
a
E DV /
J 


I
J
A


 
  DV  I 
  IR
 A 


P07124
-
Ohm’s Law
DV  IR
R

A
R has units of Ohms (W) = Volts/Amp
P07125
-
How Big is an Ohm?
• Short Copper Wire
milliohms (mW)
• Notebook paper (thru) ~1 GW
• Typical resistors
W to 100 MW
• You (when dry)
100 kW
• You (when wet)
1 kW
• Internally (hand to foot) 500 W
Stick your wet fingers in an electrical socket:
I  V / R 120 V /1kΩ
0.1A
You’re dead!
P07126
-
Appendix:
Dielectrics
P07127
-
Demonstration:
Dielectric in Capacitor
P07128
-
Dielectrics
A dielectric is a non-conductor or insulator
Examples: rubber, glass, waxed paper
When placed in a charged capacitor, the
dielectric reduces the potential difference
between the two plates
HOW???
P07129
-
Molecular View of Dielectrics
Polar Dielectrics :
Dielectrics with permanent electric dipole moments
Example: Water
P07130
-
Molecular View of Dielectrics
Non-Polar Dielectrics
Dielectrics with induced electric dipole moments
Example: CH4
P07131
-
Dielectric in Capacitor
Potential difference decreases because
dielectric polarization decreases Electric Field!
P07132
-
Dielectric Constant k
Dielectric weakens original field by a factor k
  k 0
E
Dielectric Constant
Dielectric constants
Vacuum
1.0
Paper
3.7
Pyrex Glass 5.6
Water
80
E0
k
P07133
-
Dielectric in a Capacitor
Q0= constant after battery is disconnected
Upon inserting a dielectric: V 
V0
k
Q0
Q0
Q
C 
k
 k C0
V V0 / k
V0
P07134
-
Dielectric in a Capacitor
V0 = constant when battery remains connected
Q  CV  k C0V0
Upon inserting a dielectric:
Q  k Q0
P07135
-
PRS Questions:
Dielectric in a Capacitor
P07136
-
PRS: Dielectric
A parallel plate capacitor is charged to a total charge Q
and the battery removed. A slab of material with
dielectric constant k in inserted between the plates.
The charge stored in the capacitor
+ + + + + + + +
k
15 Seconds
Remaining
- - - - - - - 0%
0%
0%
1. Increases
2. Decreases
3. Stays the Same
P07137
-
PRS Answer: Dielectric
Answer: 3. Charge stays the same
+ + + + + + + +
k
- - - - - - - -
Since the capacitor is disconnected from a
battery there is no way for the amount of
charge on it to change.
P07138
-
PRS: Dielectric
:15
A parallel plate capacitor is charged to a total charge Q
and the battery removed. A slab of material with
dielectric constant k in inserted between the plates.
The energy stored in the capacitor
+ + + + + + + +
k
- - - - - - - 0%
0%
0%
1. Increases
2. Decreases
3. Stays the Same
P07139
-
PRS Answer: Dielectric
Answer: 2. Energy stored decreases
The dielectric reduces the electric field and
hence reduces the amount of energy stored
in the field.
The easiest way to think about this is that the
capacitance is increased while the charge
remains the same so U = Q2/2C
Also from energy density:
2
uE ,0
1
1
E
2
  0 E  k 0     uE ,0
2
2
k 
P07140
-
PRS: Dielectric
A parallel plate capacitor is charged to a total charge Q
and the battery removed. A slab of material with
dielectric constant k in inserted between the plates.
The force on the dielectric
+ + + + + + + +
k
15
- - - - - - - 0%
0%
0%
1. pulls in the dielectric
2. pushes out the dielectric
3. is zero
P07141
-
PRS Answer: Dielectric
Answer: 1. The dielectric is pulled in
We just saw that the energy is reduced by the
introduction of a dielectric. Since systems
want to reduce their energy, the dielectric will
be sucked into the capacitor.
Alternatively, since opposing charges are
induced on the dielectric surfaces close to the
plates, the attraction between these will lead
to the attractive force.
P07142
-
Group: Partially Filled Capacitor
What is the capacitance of this capacitor?
P07143
-
Gauss’s Law with Dielectrics
k
E

d
A


S
qfree,in
0
P07144
-