Download PPT - LSU Physics & Astronomy

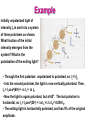
Physics 2113
Jonathan Dowling
Heinrich Hertz
(1857–1894)
Lecture 39: MON 27 APR
Ch.33 Electromagnetic Waves II
Mathematical Description of Traveling EM Waves
Electric Field:
Magnetic Field:
E = Em sin (kx - w t )
B = Bm sin (kx - w t )
Wave Speed:
c=
m0e 0
All EM waves travel a c in vacuum
Wavenumber: k =
EM Wave Simulation
1
w
=
c
2p
l
2p
Angular frequency: w =
T
Vacuum Permittivity: e 0
Vacuum Permeability:
Fig. 33-5
Amplitude Ratio:
Em
=c
Bm
Magnitude Ratio:
E (t )
=c
B (t )
m0
(33-5)
The Poynting Vector:
Points in Direction of Power Flow
Electromagnetic waves are able to transport energy from transmitter
to receiver (example: from the Sun to our skin).
The power transported by the wave and its
direction is quantified by the Poynting vector.
For a wave, since
E is perpendicular to B:
Units: Watt/m2
John Henry Poynting (1852-1914)
| S |=
1
m0
EB =
1
cm 0
E2
In a wave, the fields
change with time.
Therefore the Poynting
vector changes too!!
The direction is constant,
but the magnitude
changes from 0 to a
maximum value.
EM Wave Intensity, Energy Density
A better measure of the amount of energy in an EM wave is obtained
by averaging the Poynting vector over one wave cycle.
The resulting quantity is called intensity. Units are also Watts/m2.
I =S =
1
cm 0
___
2
E =
1
cm 0
__________ __
2
2
Em sin (kx - wt )
1
I=
Em 2 or,
2cm 0
Both fields have the
same energy density.
I=
1
cm 0
The average of sin2 over
one cycle is ½:
Erms 2
1
1
1
B2
1 B2
2
2
uE = e 0 E = e 0 (cB) = e 0
=
= uB
2
2
2 e 0 m0 2 m0
The total EM energy density is then
u = e 0 E = B / m0
2
2
Solar Energy
The light from the sun has an intensity of about 1kW/m2.
What would be the total power incident on a roof of
dimensions 8m x 20m ?
I = 1kW/m2 is power per unit area.
P=IA=(103 W/m2) x 8m x 20m=0.16 MegaWatt!!
The solar panels shown
(BP-275) has dimensions
47in x 29in. The incident
power is then 880 W. The
actual solar panel delivers
75W (4.45A at 17V): less
than 10% efficiency….
The electric meter on a solar home runs
backwards — Entergy Pays YOU!
EM Spherical Waves
The intensity of a wave is power per unit area. If one has a
source that emits isotropically (equally in all directions)
the power emitted by the source pierces a larger and
larger sphere as the wave travels outwards: 1/r2 Law!
I=
Ps
4pr
2
So the power per
unit area
decreases as the
inverse of distance
squared.
Example
A radio station transmits a 10 kW signal at a frequency of 100 MHz.
At a distance of 1km from the antenna, find the amplitude of the
electric and magnetic field strengths, and the energy incident
normally on a square plate of side 10cm in 5 minutes.
Ps
10 ´10 3 W
2
I=
=
=
0.8mW
/
m
4p r 2 4p (1´10 3m)2
1
2
I=
Em Þ Em = 2cm0 I = 0.775V/m
2cm0
Bm = Em / c = 2.58 nT
Received
energy:
I=
P DU / Dt
=
A
A
Þ DU = IADt = ( 0.8 ´ 10 -3 W / m 2 ) ( 0.1m ) ( 300s )
2
= 2.4 mJ
Radiation Pressure
Waves not only carry energy but also momentum. The effect is
very small (we don’t ordinarily feel pressure from light). If light
is completely absorbed during an interval Δt, the momentum
Transferred Δp is given by
Du
and twice as much if reflected.
Dp =
Newton’s law:
Dp
F=
Dt
c
F
A
I
Now, supposing one has a wave that hits a surface
of area A (perpendicularly), the amount of energy
transferred to that surface in time Δt will be
DU = IADt
Radiation
pressure:
IADt
D
p
=
therefore
c
IA
F=
c
I
2I
pr = (total absorption), pr =
(total reflection)
c
c
[Pa=N/m2]
The pressure p is independent
of the area A.
(a) The pressure remains the same.
The force F is proportional
to the area A.
(b) The force decreases.
Ten-micron-diameter latex beads
being propelled by a laser beam.
Radiation Pressure & Comet Tails
Solar Sails: Photons Propel Spacecraft!
StarTrek DS9
NASA Demo
NASA Concept
EM waves: polarization
Radio transmitter:
If the dipole antenna
is vertical, so will be
the electric fields. The
magnetic field will be
horizontal.
The radio wave generated is said to be “polarized”.
In general light sources produce “unpolarized
waves”emitted by atomic motions in random
directions.
EM Waves: Polarization
Completely unpolarized light will have
equal components in horizontal and
vertical directions. Therefore running the
light through a polarizer will cut the
intensity in half: I=I0/2
When polarized light hits a polarizing sheet,
only the component of the field aligned with the
sheet will get through.
E y = E cos(q )
And therefore:
I = I 0 cos 2 q
33.7: Polarization: Intensity of Polarized Light
3D Movie Glasses
Example
Initially unpolarized light of
intensity I0 is sent into a system
of three polarizers as shown.
What fraction of the initial
intensity emerges from the
system? What is the
polarization of the exiting light?
• Through the first polarizer: unpolarized to polarized, so I1=½I0.
• Into the second polarizer, the light is now vertically polarized. Then,
I2 = I1cos2(60o)= 1/4 I1 = 1/8 I0.
• Now the light is again polarized, but at 60o. The last polarizer is
horizontal, so I3 = I2cos2(30o) = 3/4 I2 =3 /32 I0 = 0.094 I0.
• The exiting light is horizontally polarized, and has 9% of the original
amplitude.
Completely unpolarized light will have
equal components in horizontal and vertical directions.
Therefore running the light through first polarizer will cut
the intensity in half: I=I0/2
I = I 0 cos2 q
When the now polarized light hits second
polarizing sheet, only the component of the
field aligned with the sheet will get through.
(a) I 0 ® I 0 ® I 0 cos (0°) = I 0
1
2
1
2
2
1
2
(b) I 0 ® 12 I 0 ® 12 I 0 cos2 (60°) = 18 I 0
(c) I 0 ® 12 I 0 ® 12 I 0 cos2 (90°) = 0
(d) I 0 ® 12 I 0 ® 12 I 0 cos2 (30°) = 83 I 0
First polarizer cuts intensity in half.
Second cuts by cos 2 q .
The q is angle between dashed lines.
100% gets through when aligned.
More gets through when more aligned.
Less gets through when less aligned.
0% gets through when at right angles.
a>d >b>c=0
Plexiglas Model of Bridge Between Crossed
Polarizers — Plastic Rotates Polarization Points of
High Stress Show Up As Close Bands of Colors