Download 3 - Rice University

Independence and Dependence
Krishna.V.Palem
Kenneth and Audrey Kennedy Professor of Computing
Department of Computer Science, Rice University
1
Contents
 In class warm up problem
 Independence and Dependence
 In-class exercise
 Conditional Probability
 Monty Hall Problem
2
Mini-Exercise 3
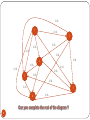
 Can you build a model for the snakes and ladder game?
 In this game, model only those transitions that cause you to
reach square 6 or less.
 If a roll caused you to go past 6, disregard the roll. There is no
need to model such a transition.
3
6
5
4
1
(Start)
2
3
 Remember the elements of a model
 The game starts at square 1.
 A node or a circle that indicates a particular square in the game
 An arrow or an edge that indicates the possibility of reaching another square
from the current square
 A label on each arrow that indicates the probability of that transition taking
place
1/6
1
2
1/6
1/6
1/6
1/6
1/6
1/6
1/6
1/6
4
1/6
1/6
5
1/6
1/6
1/6
3
6
4
1/6
Mini-Exercise - 4
 Using the model of the snakes and ladders, calculate the
following values
 The probability of reaching square 4 from square 1
 Ans: 49/216
 The probability of reaching square 5 OR square 6 from square 2
 Ans: 631/1296
 The probability of reaching square 3 AND square 5 from square
1
 Ans: 49/1296
5
Mini-Exercise - 5
Let us start with the transition model we built
1/6
1
1/6
1/6
1/6
1/6
2
1/6
1/6
4
1/6
1/6
1/6
1/6
5
1/6
1/6
1/6
3
6
6
1/6
Hint: New edge(s) might be added as an
extension.
If you land on square 6, the snake takes you
automatically to square 3. So you can never
“reach” square 6.
6
5
4
1
2
3
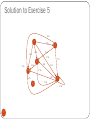
Solution to Exercise 5
1/6
1
1/6
1/6
1/6
1/6
1/6
4
1/6
1/6
1/6
2/6
1/6
1/6
5
1/6
1/6
6
7
2
3
1/6
1/6
Mini-Exercise - 6
 Using the new model of the snakes and ladders with the
snake, calculate the following values
 The probability of reaching square 4 from square 1
 Ans: 49/216
 The probability of reaching square 5 OR square 6 from square 2
 Ans: 49/216 (Remember, you cant reach 6)
 The probability of reaching square 3 AND square 5 from square
1
 Ans: 49/1296
8
Sum Rule and Relative Frequency
Consider a die D1
Consider ‘n’ rolls of D1
D1 : 1 2 4 3 6 2 4 1 5 3 3 1 3 5 2 4 6 ….
n1 = number of times D1 is 1 = 3 + …
n2 = number of times D1 is 2 = 3 + …
Relative frequency of D1 is 1 = (n1/n)
Relative frequency of D1 is 2 = (n2/n)
n6 = number of times D1 is 6 = 2 + …
Relative frequency of D1 is 6 = (n6/n)
Total = n
In the same experiment,
Neven = number of times D1 is even = 9 + …
Relative frequency of D1 is even =
(neven/n)
But neven = n2 + n4 + n6
9
Sum Rule and Relative Frequency
So relative frequency of D1 is even = (neven/n) = (n2 + n4 + n6)/n
= (n2/n) + (n4/n) + (n6/n)
Therefore relative frequency of D1 is even = relative frequency of D1 is 2 +
relative frequency of D1 is 4 +
relative frequency of D1 is 6
p(D1 is even) = p(D1 is 2 OR 4 OR 6) = p(D1 is 2) + p(D1 is 4) + p(D1 is 6)
10
Take Home Exercise - 1
 The sum rule for one die with 6 outcomes and the favorable
outcome being as an even number is
p(D1 is even) = p(D1 is 2 OR 4 OR 6) = p(D1 is 2) + p(D1 is 4) + p(D1 is 6)1
 Question: Derive the sum rule using relative frequencies
where the experiment can have K total outcomes and there
are F different favorable outcomes.
11
Contents
 In class warm up problem
 Independence and Dependence
 In-class exercise
 Conditional Probability
 Monty Hall Problem
12
Independence and Dependence
 Till now, we have been looking at events individually.
 But in practice, events are interrelated.
 Some events are dependent on some other event taking place
Let us consider the following example
Let us play a small game. Bob is rolling a die. He asks Alice to guess what he rolled.
1. What is the probability that Alice is correct ?
2. Let us say that the Oracle told Alice that the outcome of the die is an even number or
an odd number. Then what is the probability that Alice is correct ?
13
There is an underlying mathematical concept that can be explicitly stated to calculate
the answer to the question
Consider an experiment.
The outcome of the experiment can be specified in terms of two different event spaces
p
p
p1
p2
p3
Event 1
Event 2
Event 3
…
Event Even
Event Odd
Peven
Podd
…
Knowledge of the outcome of the roll of a die in terms of whether it is an even number or
an odd number allows us to predict the actual outcome more precisely
14
Let us calculate how much it improves our quality of our guess
Contents
 In class warm up problem
 Independence and Dependence
 In-class exercise
 Conditional Probability
 Monty Hall Problem
15
Exercise-5
 Let us prove this concept using an exercise
 Divide yourselves into groups of two and give yourselves the
distinguishable names Player A and Player B
 The game proceeds in two phases
 Phase 1
 Player A rolls a die
 Player B has to guess the outcome
 Phase 2
 Player A suggests to Player B whether the outcome was an odd or an even number
 Player B guesses again
 Repeat the game 20 times
 Swap the Player A and Player B rolls and repeat
16
Pseudo Random Number Generator
 For exercises of this type,
 You do not have to roll the die all the times
 You can use the pseudo random number generator at this link
http://www.random.org/integers/
 This automatically generates random numbers between the
values that you specify
17
Data
Collect the data in the following form
Roll
Guess before
suggestion
Guess after
suggestion
Correct
outcome
1
2
3
…
Consolidate data from the above table in the following form
CASE
Total number Correct
of guesses
Guesses
Without
suggestion
With suggestion
18
* Use the frequentist definition
Probability of
correct
guess*
Lessons Learnt
 What did you observe in the probabilities?
 The probability improves after some additional information
 Why do they improve ?
 Because the additional information discards some events and the size of the
event space decreases
 So what is the relation between the information and the events ?
 There is a “dependence” of the events to this information
 Can you mathematically show what the dependence is ?
The answer is “Conditional Probability”
19
Product Rule and Relative Frequency
Consider two dice, D1 and D2
Consider multiple simultaneous rolls of the two dice
D1 : 1 2 2 1 1 3 3 …..
D2 : 1 3 2 4 1 4 3 …..
p1 = number of times D1 is 1 = 3 + …
q1 = number of times D2 is 1 = 2 + …
p2 = number of times D1 is 2 = 2 + …
q2 = number of times D2 is 2 = 1 + …
p6 = number of times D1 is 6 = …
q6 = number of times D2 is 6 = …
Total = q
Total = p
r11 = number of times D1 is 1and D2 is 1 = 1 + …
r23 = number of times D1 is 2 and D2 is 3 = 1 + …
r66 = number of times D1 is 6 and D2 is 6 = …
20
Total = r
Product Rule and Relative Frequency
Consider two dice, D1 and D2
Consider multiple simultaneous rolls of the two dice
p1
r11
D1 : 1 2 2 1 1 3 3 …..
D2 : 1 3 2 4 1 4 3 …..
As the total number of trials of D1 and D2 are the same
p=q=r
The share of trials in which D2 is 1 with respect to all trials = (q1/q)
The share of trials in which D2 is 1 with respect to all trials in which D1 is 1= (r11/p1)
As the two dice are independent, for a large number of trials the share of trials in which
D2 is 1 should not be affected by the fact that D1 is 1
21
Therefore,
(q1/q) = (r11/p1)
Product Rule and Relative Frequency
Therefore, we have
(q1/q) = (r11/p1)
By rearranging the terms, r11 = p1 (q1/q)
Relative frequency of (D1 is 1, D2 is 1) = (r11/r)
= (p1 (q1/q))/r
= (p1/r) (q1/q)
= (p1/p) (q1/q)
= Relative frequency of D1 is 1 *
Relative frequency of D2 is 1
Probability of D1 is 1 AND D2 is 1 = Probability of D1 is 1 * Probability of D2 is 1
22
Take Home Exercise - 2
 The product rule for two dice with 6 outcomes for each dice
is
Probability of D1 is 1 AND D2 is 1 = Probability of D1 is 1 * Probability of D2 is 1
 Question: Derive the product rule using relative frequencies
where the there are N independent experiments with K
outcomes for each experiment.
23
Contents
 In class warm up problem
 Independence and Dependence
 In-class exercise
 Conditional Probability
 Monty Hall Problem
24
Conditional Probability
Consider the same situation
Consider an experiment.
The outcome of the experiment can be specified in terms of two different event spaces
p
pA
pB
pC
…
25
Event A
Event B
Event C
…
Event 1
Event 2
Event 3
…
p
p1
p2
p3
…
The refined probability of Event A when information about Event 1 is given
is written as P(Event A | Event 1) { read as probability of Event A given Event 1}
Consider the die
In the die example
For example, a die is rolled.
Through the knowledge of the Oracle, you know that the outcome is an even number.
What is the probability that the outcome is 2 ?
Now because there are only even numbers as possible events, the event space of the die is
Event 2
Event 4
Event 6
26
As all these events are equally likely, the probability that the
event 2 occurs is 1/3.
Conditional Probability
 Thus conditional probability can be defined as follows
 If event A is dependent on another event B, then the probability
of event A given knowledge about event B is
P(Event A | Event B) =
P(Event A and Event B occurring)
P(Event B occurring)
 For the die problem
 P(Die rolled a 2 | Die rolled an even number) =
 P(Die rolled 2 and Die rolled even) = 1/6 = 1/3!!
27
P (Die rolled even)
1/2
Intuition for conditional probability
 Let us try to find an equation for conditional probability.
 For example, let us “Event A” and “Event 1” occur simultaneously
 “Event A and Event 1 occurred simultaneously” is same as
 “Event 1 occurred” and “Event A occurring given Event 1 occurred”
(Or vice versa).
 P(Event A and Event 1 Occurred) = P(Event 1 occurred)P(Event A Occurred |
Event 1 Occurred)
 P(Event A Occurred | Event 1 Occurred) = P(Event A and Event 1 Occurred)
P(Event 1 Occurred)
Event A
Event B
Event C
…
28
Event 1
Event 2
Event 3
…
Exercise - 6
 Consider the following experiment
 There are two players involved in the game
 The first player rolls a pair of dice
 The second player has to guess the two outcomes
 Player A informs Player B of the sum
 Player B guesses again
Calculate the probability of correctness in the both the cases using conditional probability
(i) Before knowing the sum
(ii) After knowing the sum
29
Data
Collect the data in the following form
Roll
Guess before
suggestion
Guess after
suggestion
Correct
outcome
1
2
3
…
Consolidate data from the above table in the following form
CASE
Total number Correct
of guesses
Guesses
Without
suggestion
With suggestion
30
* Use the frequentist definition
Probability of
correct
guess*
Using conditional probability
 Calculate the probability of correctness in the both the cases
using conditional probability
(i) Before knowing the sum
(ii) After knowing the sum
 Recall the formula
P(Event A | Event B) = P(Event A and Event B occurring simultaneously)
P(Event B occurring)
31
First, let us try to solve the question in the conventional way using the total number of events and
the number of favorable events
Case 1: So for the first part of the question without the knowledge of the sum
Define the favorable event as Event A : (1,5)
Total number of events = 6*6 = 36
Number of favorable events = 1
Therefore,
P(Event A) = 1/36
Case 2: For the second part of the question when you know the sum,
Total number of events is less than 36 because of the knowledge of the sum
For example, Event B: Player A informs Player B that sum =6, then
the total events space is reduced to { (1,5), (2,4), (3,3), (4,2),(5,1) }
32
P(Event A |Event B) = 1/5
Now let us use conditional probability to solve for the same answer
Let
Event A: The two dice having the event guessed by Player B
Event B: The sum of the two dice being what Player A informed Player B
Using the same example of sum = 6
Let us say that Player B guessed as (1,5)
P(Event A) = 1/36 = P(Event A AND Event B)
For sum = 6
Total number of events = 36
Favorable events = (1,5), (2,4), (3,3), (4,2),(5,1)
P(Event B) = P(sum of two dice having sum as 6) = 5/36
33
P(Event A | Event B)
= P(Event A and Event B)
P(Event B)
= (1/36) / (5/36)
= 1/5
Independence and Conditional
Probability
 We introduced conditional probability to explain the
magnitude of dependence of one random variable upon
another.
 What is the conditional probability of a random variable X
given another random variable Y , if X and Y are independent
?
Let us see…
If X and Y are independent, then the outcome of Y should not have any effect on the outcome
of X.
Therefore given the information about Y, the probability of X will not be affected.
Therefore, p(X=x | Y=y) = p(X=x)
34
Independence of two random
experiments
 Two random events can be shown as independent in another
way also.
Consider two random experiments with the following event spaces
Random variable X
Event A
Event B
Event C
…
35
Random variable Y
Event 1
Event 2
Event 3
…
Recall that while discussing the method of intersection of events we mentioned that for the rule
to apply the events should be independent
The method of intersection of events stated that
“The probability of two independent events occurring simultaneously is equal to the
product of probability of individual events”
But the most important condition for that to be true is that the two events should be independent
Therefore another way of checking independence of two experiments is :
Random variables X and Y are independent if and only if
For every
36
x  X and y  Y , P( x  X , y  Y )  P( x  X )  P( y  Y )
Exercise 7
Random variable X
Event
X
probability
Random variable Y
Event
Y
probability
Head
1
0.5
Head
1
0.5
Tail
0
0.5
Tail
0
0.5
Joint experiment with Random variable X+Y
Event
probability
Head – Head
0.25
Head – Tail
0.3
Tail – Head
0.3
Tail – Tail
0.15
Can you check if the two random variables are independent using the formulation
we just discussed?
37
Contents
 In class warm up problem
 Independence and Dependence
 In-class exercise
 Conditional Probability
 Monty Hall Problem
38
Exercise 8
 The Monty Hall problem is a probability puzzle based on the
American television game show Let's Make a Deal.
Suppose you're on a game show, and you're given the
choice of three doors:
Behind one door is a car; behind the others, goats.
You pick a door, say No. 1, and the host, who knows
what's behind the doors, opens another door, say
Number 3, which has a goat.
He then says to you, "Do you want to pick door
Number 2?"
Is it to your advantage to switch your choice?
39
Developing the intuition
 Do you think the host opening the door is independent of
your choice of the door?
 Ans: NO!
 Hint:
 If you choose a door with a goat, the host MUST open the other
door with the goat
 If you choose a door with a car, the host can pick one of the 2
doors with the goat.
 So the host opening the door is DEPENDENT on your choice
of the door!!
 Now try to solve the problem!!
40
Solution
 Imagine you doing this experiment 99 times.
 Suppose you are asked to choose a door.
 No. of times you will choose a door with a goat = (99*2)/3 =
66 times.
 No. of times you will choose a door with a car = (99*1)/3 =
33 times.
 Case 1:You don’t switch
 No. of times you win the car after host opens door with a goat
= No. of times you chose a door with a car in the first place =
33 times.
 Probability of winning without switching = 33/99 = 1/3.
41
Solution
 Case 2:You switch
 Important Intuition
 Case 2.1: If you choose a door with a goat,
 The host MUST choose the other door with the goat
 As a result, the third unopened door MUST have the car.
 Clearly, switching = Winning the car
 Case 2.2: If you choose a door with a car,
 Clearly, switching does not help at all!
 Therefore, the number of times you will win if you
switch = Number of times you choose a door with a goat
in the first place = 66 times!!! (2x33 times)
 Result: Switching doubles your chance of winning!!
42
Exercise-9
 The game
 You will be given three cups
 There will be a marble under one of them.
 The rest of the two will be empty
 Divide yourselves into groups of 2
 One of the two players would be the host for the first 10 rounds
 Then swap roles
 First play 10 rounds each without changing your choice after the
first cup is opened
 Then play another 10 rounds by changing your choice
 Compare the probabilities in both the cases
43
Data
Game
First Choice First Cup
opened
Changed
choice (if
any)
1
2
3
…
44
From the above data calculate the probability of each case
(i) No change in choice
(ii) Choice changed
Second cup
opened
Correct cup
Observations
 What did you observe ?
 Was the case where you changed your choice better or worse
?
 Can you mathematically explain the correct answer to the
above question and also show by how much?
 Hint: Use conditional probabilities
45
END
46
Let us see if we can prove this using conditional probability
Define
1,2,3 = The three doors
Event C : Contestant choosing Door1
Event H : Host opening the Door 3
Before Event C and Event H
Probability(winning) = P(1 has car) = P(2 has car) = P(3 has car) = 1/3
After contestant choosing Door 1
Probability(winning | Event C) = P(1 has car) = 1/3
Probability(losing | Event C) = P(2 has car) + P(3 has car) = 2/3
47
After Event H, that is HOST opening Door 3 with a goat behind it
Now there are two choices for the contestant. Either switch or not switch
Probability(winning | Event C and Event H and Not switch) = P(1 has car) = 1/3
Probability(losing | Event C and Event H and Not switch) = P(2 has car) + P(3 has car) = 2/3
But P(3 has car) = 0
That means,
Probability(losing | Event C and Event H and Not switch) = P(2 has car) = 2/3
Therefore, as we can see that
P(1 has car) = 1/3
P(2 has car) = 2/3
It is doubly advantageous to switch choice than to stay.
48
Let us analyze this using conditional
Probability of losing
probability
= 2/3
Probability
Of winning
= 1/3
Door 1
Door 2
Door 3
Let us say that the contestant chooses Door 1
The host opens the door with the goat (say Door 3).
49
Now there are two choices for the contestant.
Either switch or stay with the previous choice.
Let us analyze both the cases.
CASE 1: If the contestant stays with the previous choice
Probability of losing
= 2/3
Probability
Of winning
= 1/3
Door 1
Door 2
Door 3
Because Door 3 has been opened. We can remove that from the choices.
50
CASE 2: If the contestant switches the choice
Probability of
losing
2/3
Probability
Of winning
1/3
Door 1
Door 2
Therefore switching choice is better than staying with the previous choice.
51