Download prairieMay05agu

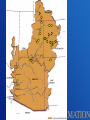
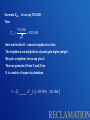
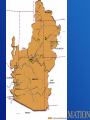
A stochastic nonparametric
technique for space-time
disaggregation of streamflows
May 27, 2005
2005 Joint Assembly
Agenda
•
•
•
•
•
•
•
•
Motivation
Current Methods
Proposed Technique
Step Through Solution
Application
Results
Conclusion
Next Steps
Motivation
• Develop realistic streamflow scenarios at
several sites on a network simultaneously
• Difficult to model the network from
individual gauges
9
10
11
13
12
14
15
1
2
8 3
16
7
17
6
19
20
18
4
5
Motivation
• Present methods can not capture higher order
features
• Present methods can be difficult to implement
• Can not easily incorporate climate information
• Finding the probability of events
• Required for long-term basin-wide planning
– Develop shortage criteria
– Meeting standards for salinity
Current Methods
• Parametric
– Valencia and Schaake, 1972
• Basic form
–
–
–
–
Mejia and Rousselle, 1976
Lane, 1979
Salas et al. 1980
Stedinger and Vogel, 1984
• Nonparametric
– Tarboton et al. 1998
– Kumar et al. 2000
X  AZ  Bε
Drawbacks of Parametric
• Data must be transformed to a normal
distribution
– During transformation additivity is lost
• There are many parameters to estimate
– Al least 36 parameters for annual to monthly
• Inability to capture non-Guassian and nonlinear features
Basic Problem
• Resampling from a conditional PDF
f (X Z) 
f (X , Z)
 f ( X , Z )dX
Joint probability
Marginal probability
• Where Z is the annual flow
X are the monthly flows
• Or this can be viewed as a spatial problem
– Where Z is the sum of d locations of monthly flows
X are the d locations of monthly flow
Steps for Temporal Disagg
Step 1
Transform
monthly flow
X with
rotational
matirx R such
that XR=Y
Step 2
Generate an
annual flow
vector Z with
an appropriate
model
Step 3
Build a matrix
U where the
first 11
columns are
from Y and the
final column is
Z’, where
Z’ = Z/√12
Steps for Temporal Disagg
Step 4
Resample a
vector u from
the conditional
PDF f(U|Z)
Step 5
Back transform
the resampled
u such that
uRT = X
monthly values
X
X are the
monthly values
that add to Z
Observed data at 2 gauges for 2 years
Gauge 1
Gauge 2
Gauge 1 +2
221 .6942 232 .0874   453 .7816 
X 

Z


584 .6528 1206 .0435  1790 .6963 
Solve for R with Gram Schmidt orthonormalization
 0.7071068
R
 0.7071068
0.7071068 
0.7071068 
  7.349112
Y  RX  
 439 .389556
320 .8721 
1266 .2134 
Note the last column of
R = 1/√d
RT = R-1
Generate Zsim let us say 735.6541
Then
Z ' sim 
735 .6541
 520 .1860
2
Next we find the K – nearest neighbors to Zsim
The neighbors are weighted so closest gets higher weight
We pick a neighbor, let us say year 2
Then we generate U from Y and Z’sim
U is a matrix of nyears by dstations
U  Y(1,...,dstation1) , Z ' sim    439 .3896
520 .1860 
Via back rotation we can solve for the
disaggregated components of Zsim
 0.7071068
X sim  R T U  
 0.7071068
 57 .13172 
X sim  

678
.
52238


T
0.7071068 
 439 .3896

0.7071068 
520 .1860 
Note the disaggregated components add to Zsim = 735.6541
The only key parameter is K
which is estimated with a heuristic scheme K=√N
Application
• The Upper Colorado River Basin
– 4 key gauges
• Perform 500 simulations each of 90 years
length
• Annual Model
– a modified K-NN lag-1 model
Results
• Basic Statistics
– Lower order: mean, standard deviation, skew,
autocorrelation (lag-1)
• Extended Statistics
– Higher order: probability density function,
drought statistics
• We provide some comparison with a
parametric disaggregation model
3
16
19
20
Bluff
Lees Ferry
Bluff gauge
June flows
Nonparametric
Parametric
Lees Ferry Gauge
May Flows
Nonparametric
Parametric
Lees Ferry Gauge
Drought
Statistics
Annual Model
Modified K-NN
lag-1
Annual Model
18 year block
bootstrap
Conclusions
•
•
•
•
•
•
•
No need for data transformation
Limited parameters
Preserves basic statistics
Preserves summability
Preserves arbitrary PDF
Preserves cross correlation
Simple to implement
Next Steps
• Simulate policy and discuss results
• Analysis paleo-streamflows
– Data analysis
– Transition Probability Matrix
• Conditioning on climate
A stochastic nonparametric
technique for space-time
disaggregation of streamflows
For further information:
http://cadswes.colorado.edu/~prairie