* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download No Slide Title - Brigham Young University
Survey
Document related concepts
Transcript
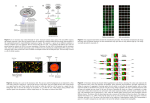
Microarray data analysis 25 January 2006 David A. McClellan, Ph.D. Introduction to Bioinformatics [email protected] Brigham Young University Dept. Integrative Biology Inferential statistics Inferential statistics are used to make inferences about a population from a sample. Hypothesis testing is a common form of inferential statistics. A null hypothesis is stated, such as: “There is no difference in signal intensity for the gene expression measurements in normal and diseased samples.” The alternative hypothesis is that there is a difference. We use a test statistic to decide whether to accept or reject the null hypothesis. For many applications, we set the significance level a to p < 0.05. Page 199 Inferential statistics A t-test is a commonly used test statistic to assess the difference in mean values between two groups. t= x1 – x2 s difference between mean values = variability (noise) Questions Is the sample size (n) adequate? Are the data normally distributed? Is the variance of the data known? Is the variance the same in the two groups? Is it appropriate to set the significance level to p < 0.05? Page 199 Inferential statistics Paradigm Parametric test Nonparametric Compare two unpaired groups Unpaired t-test Mann-Whitney test Compare two paired groups Paired t-test Wilcoxon test Compare 3 or more groups ANOVA Page 198-200 ANOVA ANalysis Of VAriance ANOVA calculates the probability that several conditions all come from the same distribution Parametric vs. Nonparametric Parametric tests are applied to data sets that are sampled from a normal distribution (ttests & ANOVAs) Nonparametric tests do not make assumptions about the population distribution – they rank the outcome variable from low to high and analyze the ranks Mann-Whitney test (a two-sample rank test) Actual measurements are not employed; the ranks of the measurements are used instead n1 n1 1 U n1n2 R1 2 n1 and n2 are the number of observations in samples 1 and 2, and R1 is the sum of the ranks of the observations in sample 1 Mann-Whitney example Mann-Whitney table Wilcoxon paired-sample test A nonparametric analogue to the pairedsample t-test, just as the Mann-Whitney test is a nonparametric procedure analogous to the unpaired-sample t-test Wilcoxon example Wilcoxon table Inferential statistics Is it appropriate to set the significance level to p < 0.05? If you hypothesize that a specific gene is up-regulated, you can set the probability value to 0.05. You might measure the expression of 10,000 genes and hope that any of them are up- or down-regulated. But you can expect to see 5% (500 genes) regulated at the p < 0.05 level by chance alone. To account for the thousands of repeated measurements you are making, some researchers apply a Bonferroni correction. The level for statistical significance is divided by the number of measurements, e.g. the criterion becomes: p < (0.05)/10,000 or p < 5 x 10-6 Page 199 Significance analysis of microarrays (SAM) SAM -- an Excel plug-in -- URL: www-stat.stanford.edu/~tibs/SAM -- modified t-test -- adjustable false discovery rate Page 200 Page 202 observed upregulated expected downregulated Page 202 Descriptive statistics Microarray data are highly dimensional: there are many thousands of measurements made from a small number of samples. Descriptive (exploratory) statistics help you to find meaningful patterns in the data. A first step is to arrange the data in a matrix. Next, use a distance metric to define the relatedness of the different data points. Two commonly used distance metrics are: -- Euclidean distance -- Pearson coefficient of correlation 203 Euclidean Distance Pearson Correlation Coefficient Descriptive statistics: clustering Clustering algorithms offer useful visual descriptions of microarray data. Genes may be clustered, or samples, or both. We will next describe hierarchical clustering. This may be agglomerative (building up the branches of a tree, beginning with the two most closely related objects) or divisive (building the tree by finding the most dissimilar objects first). In each case, we end up with a tree having branches and nodes. Page 204 Agglomerative clustering 0 1 2 3 4 a b a,b c d e Page 206 Agglomerative clustering 0 1 2 3 4 a b a,b c d e d,e Page 206 Agglomerative clustering 0 1 2 3 4 a b a,b c d e c,d,e d,e Page 206 Agglomerative clustering 0 1 2 3 4 a b a,b a,b,c,d,e c d e c,d,e d,e …tree is constructed Page 206 Divisive clustering a,b,c,d,e 4 3 2 1 0 Page 206 Divisive clustering a,b,c,d,e c,d,e 4 3 2 1 0 Page 206 Divisive clustering a,b,c,d,e c,d,e d,e 4 3 2 1 0 Page 206 Divisive clustering a,b a,b,c,d,e c,d,e d,e 4 3 2 1 0 Page 206 Divisive clustering a b a,b a,b,c,d,e c c,d,e d d,e e 4 3 2 1 0 …tree is constructed Page 206 agglomerative 0 1 2 3 4 a b a,b a,b,c,d,e c c,d,e d d,e e 4 3 2 1 0 divisive Page 206 1 12 1 12 Page 207 Cluster and TreeView Page 208 Cluster and TreeView clustering K means SOM PCA Page 208 Cluster and TreeView Page 208 Cluster and TreeView Page 208 Page 208 Page 208 Page 208 Two-way clustering of genes (y-axis) and cell lines (x-axis) (Alizadeh et al., 2000) Page 209 Self-Organizing Maps (SOM) To download GeneCluster: http://www.genome.wi.mit.edu/MPR/software.html SOMs are unsupervised neural net algorithms that identify coregulated genes Page 211 Two pre-processing steps essential to apply SOMs 1. Variation Filtering: Data are passed through a variation filter to eliminate those genes showing no significant change in expression across the k samples. This step is needed to prevent nodes from being attracted to large sets of invariant genes. 2. Normalization: The expression level of each gene is normalized across experiments. This focuses attention on the 'shape' of expression patterns rather than absolute levels of expression. Principal components analysis (PCA) An exploratory technique used to reduce the dimensionality of the data set to 2D or 3D For a matrix of m genes x n samples, create a new covariance matrix of size n x n Thus transform some large number of variables into a smaller number of uncorrelated variables called principal components (PCs). Page 211 Principal component axis #2 (10%) Principal components analysis (PCA), an exploratory technique that reduces data dimensionality, distinguishes lead-exposed from control cell lines P4 N2 Legend Lead (P) C2 P1 N3 C3 P2 P3 C4 N4 Sodium (N) Control (C) C1 Principal component axis #1 (87%) Principal components analysis (PCA): objectives • to reduce dimensionality • to determine the linear combination of variables • to choose the most useful variables (features) • to visualize multidimensional data • to identify groups of objects (e.g. genes/samples) • to identify outliers Page 211 http://www.okstate.edu/artsci/botany/ordinate/PCA.htm Page 212 http://www.okstate.edu/artsci/botany/ordinate/PCA.htm Page 212 Page 212 Use of PCA to demonstrate increased levels of gene expression from Down syndrome (trisomy 21) brain Chr 21