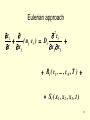Download 637_diffusion

Atmospheric Dispersion (AD)
Matus Martini
Seinfeld & Pandis: Atmospheric Chemistry and Physics
Nov 29, 2007
1
Outline
• Eulerian approach
• Lagrangian approach
eqns for mean concentration, solutions for
instantaneous and continuous source
• Gaussian plume eqn
AD parameterizations (P-G curves), plume
rise
2
Air pollution dispersion models
• Box model air pollutants inside the box are
homogeneously distributed
• Gaussian model is perhaps the oldest (circa 1936)
• Lagrangian model - statistics of the trajectories of a
large number of the pollution plume parcels.
• Eulerian model - fixed three-dimensional Cartesian grid
• Dense gas model
• Hybrids (Plume in Grid model)
3
Leonhard Euler (1707-1783) v. Joseph Louis Lagrange (1736-1813)
4
Lagrange v. Euler
•PROS over Eulerian models:
– no Courant number restrictions
– no numerical diffusion/dispersion
– easily track air parcel histories
– invertible with respect to time
•CONS:
– need very large # points for statistics
– inhomogeneous representation of domain
– convection is poorly represented
– nonlinear chemistry is problematic
Embedding Lagrangian plumes in Eulerian models (PinG model):
Release puffs from point sources and transport them along
trajectories, allowing them to gradually dilute by turbulent mixing
(“Gaussian plume”) until they reach the Eulerian grid size at which
5
point they mix into the gridbox
6
7
Eulerian approach
c i
 ci


( u j ci )  Di

t  x j
x j x j
2
 Ri ( c1 , ... , c N , T ) 
 S i ( x1 , x 2 , x 3 , t )
8
Eulerian approach
• If we assume that the presence of small concentration species does
not affect the meteorology to any detectable measure, the continuty
eqn can be solved independently of the coupled momentum and
energy eqns
• 1. sufficient heat can be generated by chemical reactions to
influence the temperature
• 2. absorption, reflection, and scattering of radiation by trace
gases and particles could result in alterations of the fluid behavior
• The flow of interest is turbulent, the fluid velocities uj are random
functions of space and time:
• deterministic and stochastic component of velocity u j  u j  u' j
9
Eulerian approach
• since u’j is random ci resulting from the solution must also be
random -> probability density function for a random process as
complex as AD is almost never possible -> mean of ensemble of
realizations <ci>
• convenient to express ci as <ci> + c’i where by definition <ci’> = 0
• If the single species decays by a 2nd - order reaction:
<R> = - k ( <c>2 – <c’2>)
• closure problem (emergence of new dependent variables <c’2>)
• Eulerian description of turbulent diffusion will not permit exact
solution even for the mean concentration <c>
10
Lagrangian approach
• behavior of representative fluid particles
• consider a single particle located at location x’ at time t’ in a
turbulent fluid
• trajectory of the subsequent motion: X[x’,t’;t] at any later time t
• probability density function

 ( x, t ) 





Q( x , t | x' , t' ) ( x' , t' ) dx'
integrated over all possible starting points x’
• Q(x, t | x’, t’) transition probability density: the particle originally at
x’, t’ will undergo a displacement to x at t
11
Lagrangian approach
• Ensemble mean concentration:

c( x , t ) 

 i ( x , t )
• General formula for the mean concentration:

c( x , t ) 
t








 Q( x , t | x0 , t 0 ) c( x0 , t 0 ) dx0    Q( x , t | x' , t' )S ( x' , t' )dt' dx'
t0
particles present at t0
added from sources between t0 and t
• We need complete knowledge of the turbulence properties -> Q
• Except the simplest circumstances Q is unavailable!
• Integrals hold only when no undergoing chemical reactions,
conservative species!
12
• Eulerian statistics are readily measurable (fixed network
of anemometers)
• can include detailed chemical mechanisms
• serious mathematical obstacle: closure problem
• Lagrangian – displacements of groups of particles
released in the fluid
• difficulty of accurately determining the required particle
statistics: not directly applicable to problems involving
nonlin chem reactions
• Exact solution for the mean concentration even of inert
species in a turbulent fluid is not possible in general!
• Approximations
13
Mean concentration – K theory
• Eulerian approach: approx AD eqn
• Molecular diffusion is negligible compared with turbulent
diffusion
2
 c

Di

u j' c'
x j x j
x j
• linearization: incompressible atmosphere
• Ri almost always nonlin, the most obvious approx:
Ri ( c1 , ... , c N ,T )  Ri ( c1 , ... , c N , T )
ci
ci

 uj

t
x j
x j

 ci 
 K jj
  Ri ( c1 , ... , c N , T )  S i ( x , t )

x j 

• reaction processes are slow compared w/turbulent transport
14
• distribution of sources is “smooth” (violated near strong isolated sources)
Mean concentration – statistical theory
• Lagrangian approach: stationary, homogeneous Gausian flow
• In highly idealized example: u(t) is a random variable
depending only on time, and is stationary, Gaussian
random proces, u(t) pdf
 ( u  u )2 
1
pu ( u ) 
exp 
2  u

2 u
2



• stationarity implies that the statistical properties of u at
two different times depend only on t–t and not on t and t
individually, transition probabilty density


 
Q( x , t | x' , t' )  Q( x  x' , t  t' )
• Then mean concentration is itself Gaussian (!):
c( x , t ) 
 ( x  u t )2
exp 
2
2

2  x ( t )
x (t )

1




15
Instantaneous point source
• Eulerian approach
• eddy diffusivities Kxx, Kyy, Kzz = const
 c
t
u
 c
x
 K xx
2 c
x
2
 K yy
2 c
y
2
 K zz
2 c
z 2
c( x , y , z , 0 )  S  ( x )  ( y )  ( z )
c( x , y , z , t )  0
x , y , z  
Solution:
c( x , y , z , t ) 
8 t 
S
3/ 2
K xx K yy K zz
2
2
 ( x  u t )2

y
z


exp 



4 K xx t
4 K yy t 4 K zz t 

16
Instantaneous point source
• If we define:
 x2  2 K xx t
 y2  2 K yv t
 z2  2 K zz t
the two expressions are identical
• Evidently, there is a connection between Eulerian and
Lagrangian approaches
17
Continuous source, steady state
• Lagrangian approach
• Source began emitting at t = 0, mean concentration
achieves a steady state (independent of time), and source
S ( x , y , z ,0 )  q ( x ) ( y ) ( z )
strength q in [g s-1]:


c( x , t )  lim c( x , t )  lim
t 
t 


 Q( x , t | 0 , t' ) q dt'
t
0




Q( x , t | 0 , t' )  Q( x' , t  t' | 0 , 0 )
slender plume approx: advection dominates plume dispersion
(neglecting diffusion in the direction of the mean flow)
2
2 

q
y
z

c( x , y , z ) 
exp  

2
2
 2
2 u  y z
2 z 
y

18
Continuous point source, steady state
• Eulerian approach
u
 c
x
Solution:
 2 c
2 c
2 c
 K 


2
2
2

x

y

z

c( x , y , z , t ) 

  q  ( x ) ( y ) ( z )


 u ( r  x )
q

exp 
4 K r
2K 

2
2
2
2
where r  x  y  z
slender plume approx: interest only in the plume centerline
2 
 u  y2
q
z


c( x , y , z , t ) 
exp  

1/ 2

4 K yy K zz
x
 4 x  K yy K zz  


2
Lagrangian and Eulerian expressions are identical if  y 
2 K yy x
u
, z 
2
2 K zz x
u
19
Recapitulation
• Lagrangian and Eulerian solutions are identical if
• Instantaneous point source
 x2  2 K xx t
 y2  2 K yv t
 z2  2 K zz t
• Continuous point source
y 
2
2 K yy x
u
, z
2
2 K zz x

u
• In most applications of the Lagrangian formulas, the
dependence of y2 and z2 on x are determined
empirically
• Relationship between K theory and the Gaussian
formulas
20
Summary of AD theories, Lagrange / Euler
• So far only physical processes responsible for the dispersion of a
cloud or a plume due to only velocity fluctuations (instantaneous or
continuous source in idealized stationary, homogeneous turbulence)
• Because of the inherently random character of atmospheric motions,
one can never predict with certainity the distribution of concentration
of marked particles emitted from a source. Although the basic
equations describing turbulent diffusion are available, there does not
exist a single mathematical model that can be used as a practical
means of computing atmospheric concentrations over all ranges of
conditions.
• The deciding factor in judging the validity of a theory for atmospheric
diffusion is the comparison of its predictions with experimental data.
Theory gives ensemble mean concentration <c>, whereas a single
experimental observation constitues only one sample from the
hypothetically infinite ensemble of observations. (It’s practically
impossible to repeat an experiment more than a few times under
identical conditions in the atmosphere.)
21
22
Gaussian spreading
in 2D have
a binormal distribution
23
Plume rise Dh
H – effective stack height
24
Gaussian Plume Equation
• Lagrangian approach: under certain idealized conditions (stationary,
homogeneous turbulence), the mean conc. of species emitted from
a point source has a Gaussian distribution
 ( x  x'  u ( t  t' ))2 ( y  y' )2 ( z  z' )2 

Q( x , y , z , t | x' , y' , z' , t' ) 
exp  


2
2
2
3/ 2

( 2 )  x y z
2 x
2 y
2 z 

1
• in the slender plume case x -> 0
c( x , y , z ) 
2 

y

f  exp  
 2 2 
y 

g  g2  g3
q
f

 1
u  y 2
 z 2
 ( z  H )2 

g1  exp  
2


2 z


 ( z  H )2 

g 2  exp  
2


2 z


f - crosswind dispersion
g – vertical dispersion: g1 – no reflections, g2 – reflection from the
ground, g3 - reflection from an inversion aloft
q – emission rate, H – effective stack height
25
26
Gaussian Plume Equation
• Eulerian approach: It can be shown (use of Green function)
that we can get to the same result by solving the AD eqn (but
with const eddy diffusivities)!
Johann Carl Friedrich Gauss
(1777-1855)
27
Dispersion parameters in Gaussian models
• Derived from concentrations measured in actual atmospheric diffusion
experiments
 z   w t Fz
 y   v t Fy
where v , w are standard deviations of the wind velocity fluctuations
Fy , Fz characterize PBL:
friction velocity u*, convective velocity scale w*
Monin-Obukhov length L
Coriolis parameter f
mixed layer depth zi (upper boundary, the height of an elevated layer
impermeable to diffusion)
• surface roughness z0
• height of pollutant release above the ground H
•
•
•
•
•
•
28
AD Parameterizations
• From two standard deviations more is known about y , since
most experiments are ground-level. Vertical concentration
distributions are needed to determine z
• Ground-leveled releases are not exactly gaussian in vertical.
• For complete parameterization we need all these variables
• not always available!
• Pasquill stability categories A – F
(1961)
Surface windspeed
Daytime incoming solar radiation
Nighttime cloud cover
• Correlations for sigmas based on readily available ambient data!
29
AD Parameterizations
Pasquill
stability
classes
30
Pasquill-Gifford (P-G) curves
Horizontal  y
and
vertical  z dispersion coeff
Distance from source [m]
31
Behavior of a plume
• initial source conditions: exit velocity,Tplume – Tair
• stratification
• wind speed
• gases are usually released at T hotter than the
ambient air and are emitted with considerable initial
momentum
Buoyant plume
Forced plume
Jet
Initial buoyancy >> initial momentum
Initial buoyancy ~ initial momentum
Initial buoyancy << initial momentum
32
Analytical properties of Gaussian Plume Eqn
• along the centerline (y=0) at the ground (z=0)
• we need effective stack height H !!
 H2 

c( x , 0 , 0 ) 
exp  
2
 2 
 u  y z
z 

q
Maximum ground-level concentration
• derivative w.r.t x = 0
critical downwind distance xc , critical wind speed uc
33
Critical downwind distance
as a function of source height and a stability class
(plume that has reached its final height)
no xc for stable stratification!
34
Summary 3
Gaussian expressions
fail near the surface, since no vertical shear is present
no chemical reactions, either
Eulerian approach
AD eqn provides more general approach (special cases: uniform wind
speed and constant eddy diffusivities), key problem is to choose the
functional forms of the wind speeds and the eddy diffusivities
•
•
•
Generally, exact solution for the mean concentration even of inert
species in a turbulent fluid is not possible!
Therefore: approximations, K-theory, linearizations
in stationary, homogeneous Gausian flow: the solution for <c> is itself
Gaussian!
Instantaneous and continuous point source: stationary, homogeneous
turbulence, and const eddy diffusivities -> Gaussian plume eqn
(Lagrange agrees with Euler)
•
•
Experimental data –> parameterizations, P-G curves convenient for
determining y , z
We saw why the stack height and PBL meteorology matter.
35