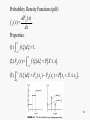Download Signals and Systems

Lecture 12
Overview of Probability and Random
Variables (I)
Fall 2008
NCTU EE
Tzu-Hsien Sang
1
Outline
•
•
•
•
•
What is Probability
Random Variables
Distribution Functions
Multiple Variables
Statistical Averages
2
What is Probability
• Why probabilistic analysis?
• My answer: to To hold on something in a world full of chaos
and uncertainties
Applications
• Engineering
Systems and control (e.g., aircraft control), Decision and
resource allocation under uncertainty (e.g., communications
networks), Reliability (noise, error control, failures)
•
•
•
•
Economics and finance
Physics, statistical mechanics, thermodynamics
Medicine, FDA, drugs and procedures
Linguistics, automatic speech recognition and translation
3
• In this course, both messages (signals) & noises can
be treated as random in nature.
Q: What benefits can we get from doing that?
• Some definitions:
(a) random variable (r.v.): one random quantity
(b) random sequence: sequence of random variable
(c) random process: a (continuous-time) function
whose value (at any time instant) is a r.v.
4
A Basic Probabilistic model: an experiment means a
mathematical model of a process with an outcome
that is not fully predictable
Basic Components:
• Outcome: each experiment produces exactly one
outcome
• Sample space: A list of all outcomes of an experiment
• Algebra of events (set theory): language for
manipulating collections of elementary events = sets
• Probability law: means of assigning a probability to
events in a consistent and useful way
5
6
How to establish a probabilistic model?
•
•
•
Relative Frequency --- experimental, intuitive,
Axiomatic Theory --- mathematical, rigorous,
facilitate further derivation (most importantly, it can
deal with infinity!)
Example: Tossing two fair coins (Please list the
events, sample space, probability law, etc.)
7
• Probability Theory (I)
  Sample space (a collection of elementary events)
  A collection of subsets of  and forms a filed (a  -field)
Remarks:
(1) (, ) defines a field, if
(a)    and   .
(b) For any A, B  , A  B  .
(c) For any A  , then Ac    A  .
(2)  -field: Consider countably infinite  and  .
If Ai  , then

i 1
Ai   and

i 1
Ai  .
8
• Probability Theory (II)
A probability space is defined by a triplet (, , P).
(i) (, ) is a  -field.
(ii) P is a probability measure.
Remarks:
is a probability measure on  if
(a) For any A  , P( A)  0.
(b) P( )  0 and P()  1.
(c) For any A, B  , if A  B   , then P( A  B)  P( A)  P( B)
(d)  -additivity: For Ai   and if Ai  Aj   for all i  j,

then P(
i 1

Ai )   P( Ai ).
i 1
9
Math Models and Reality
• Models are purely mathematical creations. There is
no guarantee that they can “fit” the reality well
enough.
• You need to balance among accuracy, simplicity, and
tractability.
• For many cases, difficulties arise from fuzzy word
usage in the formulation of the problem.
• Example Bertrand’s “paradox” (1889)
Consider a “randomly drawn” chord of a circle. What
is the probability that its length is greater than a
certain length?
10
Random Variables
Definition: Given a probability space (, , P), a r.v. is a
mapping X :   R such that
(i) the set { : X ( )  B} must be a legal event A in for any
Borel set B in R.
(ii) P( X  )  P( X  )  0.
Note: Borel set means a set in the smallest  -field that contains
all of the open sets in R. (  all kinds of intervals on the real line.)
11
 Remarks:
(1) ( R,{B}, P) is a derived probability space from the original
probability space (, , P) ).
If X ( ) is properly defined (selected), ( R,{B}, P) reflects all the
probabilistic properties of (, , P). But ( R,{B}, P) is often
easier to handle (because of real line).
(2) A random variable X ( ) is a function (mapping) not a simple
value.
(3) Notations:
Capital letters  random variable: X , Y ,  ...
Lower-case letters  values of random variable: x, y,  ...
12
Distribution Functions
Probability (Cumulative) Distribution Functions (PDF or cdf)
FX ( x)  P[ X  x], where { X  x}  { : X ( )  x}.
Properties:
(1) FX ()  0, FX ()  1.
(2) Continuous from right: lim x x  FX ( x )  FX ( x0 ).
0
(3) Nondecreasing: FX ( x1 )  FX ( x2 ) if x1  x2 .
13
Probability Density Functions (pdf)
dFX ( x)
f X ( x) 
.
dx
Properties:
(1)



f ( )d  1.
(2) FX ( x)  
x

(3)

x2
x1
f ( )d  P[ X  x].
f ( )d  FX ( x2 )  FX ( x1 )  P[ x1  X  x2 ].
14
Example pdfs
• Binomial distribution
Remarks: the Laplace approximation to the binomial distribution
Pn (k ) 
1
(k  np) 2
exp[
].
2npq
2 npq
15
 Poisson distribution
( T ) T
For  >0, PT (k ) 
e
for k = 0, 1, 2, ...
k!
When n is large and p is small
k
( K )k  K
Pn (k ) 
e , where K  E[ K ].
k!
16
• Gaussian (normal) distribution
17
Multiple Variables
 Joint cdf's and pdf's
P ( X  x, Y  y ).
FXY ( x, y )
 2 FXY ( x, y )
f XY ( x, y ) 
.
xy
P( x1  X  x2 , y1  Y  y2 )  
y2
y1

x2
x1
f XY ( x, y )dxdy.
Marginal distribution:
FX ( x)  FXY ( x, )  FXY ( x, Y  )
FY ( y )  FXY (, y )  FXY ( X  , y )
f X ( x)  


f XY ( x, y )dy.
18
19
• Conditional Probability: a derived probability
measure
• Conditional cdf and pdf:
• Conditional random variables:
20
 Independent r.v.
P( X  x, Y  y )  P( X  x) P(Y  y ).
FXY ( x, y )  FX ( x) FY ( y ).
f XY ( x, y )  f X ( x) fY ( y ).
Example: 2-D Gaussian
21
Bayes’ Theorem
• Objective: Inference instead of prediction or
observation
• Given observed “effect" or “result", infer the
unobserved “cause". Assume we know the
“prior" or “a priori" probabilities and the
conditional probabilities in order to compute
the “posterior" or “a posteriori" probabilities.
22