Download coppin chapter 12e

Chapter 12
Probabilistic Reasoning and
Bayesian Belief Networks
1
Chapter 12 Contents









Probabilistic Reasoning
Joint Probability Distributions
Bayes’ Theorem
Simple Bayesian Concept Learning
Bayesian Belief Networks
The Noisy-V Function
Bayes’ Optimal Classifier
The Naïve Bayes Classifier
Collaborative Filtering
2
Probabilistic Reasoning

Probabilities are expressed in a
notation similar to that of predicates
in FOPC:
P(S) = 0.5
P(T) = 1
P(¬(A Λ B) V C) = 0.2

1 = certain; 0 = certainly not
3
Conditional Probability

Conditional probability refers to the
probability of one thing given that we
already know another to be true:

This states the probability of B, given
A.
4
Conditional Probability
Note that P(A|B) ≠ P(B|A)
 P(R/\S) = 0.01
 P(S) = 0.1
 P(R) = 0.7

5
Conditional Probability
Conditional probability refers to the
probability of one thing given that we
already know another to be true:
P(A \/ B) = P(A) + P(B) – P(A /\ B)
P(A /\ B) = P(A) * p(B) if A and B are
independent events.

6
Joint Probability Distributions



A joint probability distribution represents
the combined probabilities of two or more
variables.
This table shows, for example, that
P (A Λ B) = 0.11
P (¬A Λ B) = 0.09
Using this, we can calculate P(A):
P(A) = P(A Λ B) + P(A Λ ¬B)
= 0.11 + 0.63
= 0.74
7
Bayes’ Theorem

Bayes’ theorem lets us calculate a
conditional probability:
P(B) is the prior probability of B.
 P(B | A) is the posterior probability of
B.

8
Baye’s Thm
P(A/\B) = P(A|B) P(B) dependent events
 P(A/\B) = P(B /\ A) = P(B|A) P(A)
 P(A|B) P(B) = P(B|A) P(A)

P(A|B) P(B)

P(B|A) = -----------P(A)
9
Simple Bayesian Concept Learning (1)




P (H|E) is used to represent the probability that
some hypothesis, H, is true, given evidence E.
Let us suppose we have a set of hypotheses
H1…Hn.
For each Hi
Hence, given a piece of evidence, a learner can
determine which is the most likely explanation by
finding the hypothesis that has the highest
posterior probability.
10
Simple Bayesian Concept Learning (2)





In fact, this can be simplified.
Since P(E) is independent of Hi it will have the
same value for each hypothesis.
Hence, it can be ignored, and we can find the
hypothesis with the highest value of:
We can simplify this further if all the
hypotheses are equally likely, in which case we
simply seek the hypothesis with the highest
value of P(E|Hi).
This is the likelihood of E given Hi.
11
Example







If high temp (A), have cold (B) – 80%
P(A|B) = 0.8
Suppose 1 in 10,000 have cold
Suppose 1 in 1,000 have high temp
P(A) = 0.001 P(B) = 0.0001
P(B|A) = {P(A|B)*P(B)}/P(A)
= 0.008 8 chances in 1000 that you
have a cold when having a high temp.
12
Bayesian Belief Networks (1)




A belief network shows the dependencies
between a group of variables.
If two variables A and B are independent if the
likelihood that A will occur has nothing to do
with whether B occurs.
C and D are dependent on A; D and E
are dependent on B.
The Bayesian belief network has
probabilities associated with each link.
E.g., P(C|A) = 0.2, P(C|¬A) = 0.4
13
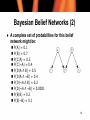
Bayesian Belief Networks (2)

A complete set of probabilities for this belief
network might be:










P(A) = 0.1
P(B) = 0.7
P(C|A) = 0.2
P(C|¬A) = 0.4
P(D|A Λ B) = 0.5
P(D|A Λ ¬B) = 0.4
P(D|¬A Λ B) = 0.2
P(D|¬A Λ ¬B) = 0.0001
P(E|B) = 0.2
P(E|¬B) = 0.1
14
Bayesian Belief Networks (3)



We can now calculate conditional probabilities:
P(A,B,C,D,E) = P(E|A,B,C,D)*P(A,B,C,D)
In fact, we can simplify this, since there are
no dependencies between certain pairs of
variables – between E and A, for example.
Hence:
15
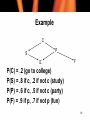
Example
C
P
S
E
F
P(C) = .2 (go to college)
P(S) = .8 if c, .2 if not c (study)
P(P) = .6 if c, .5 if not c (party)
P(F) = .9 if p, .7 if not p (fun)
16
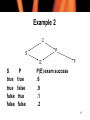
Example 2
C
P
S
E
S
true
true
false
false
P
true
false
true
false
F
P(E) exam success
.6
.9
.1
.2
17
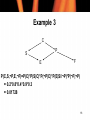
Example 3
C
P
S
E
F
P(C,S,¬P,E,¬F)=P(C)*P(S|C)*P(¬P|C)*P(E|S/\¬P)*P(¬F|¬P)
= 0.2*0.8*0.4*0.9*0.3
= 0.01728
18
Bayes’ Optimal Classifier





A system that uses Bayes’ theory to classify data.
We have a piece of data y, and are seeking the
correct hypothesis from H1 … H5, each of which
assigns a classification to y.
The probability that y should be classified as cj is:
x1 to xn are the training data, and m is the number
of hypotheses.
This method provides the best possible
classification for a piece of data.
19
The Naïve Bayes Classifier (1)





A vector of data is classified as a single classification.
p(ci| d1, …, dn)
The classification with the highest posterior probability is
chosen.
The hypothesis which has the highest posterior
probability is the maximum a posteriori, or MAP
hypothesis.
In this case, we are looking for the MAP
classification.
Bayes’ theorem is used to find the posterior
probability:
20
The Naïve Bayes Classifier (2)

since P(d1, …, dn) is a constant, independent of ci,
we can eliminate it, and simply aim to find the
classification ci, for which the following is
maximised:

We now assume that all the attributes d1, …, dn are
independent
So P(d1, …, dn|ci) can be rewritten as:


The classification for which this is highest is chosen to
classify the data.
21
Collaborative Filtering



A method that uses Bayesian
reasoning to suggest items that
a person might be interested in,
based on their known interests.
if we know that Anne and Bob
both like A, B and C, and that
Anne likes D then we guess
that Bob would also like D.
Can be calculated using
decision trees:
22