Download Slide 1

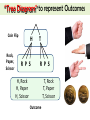
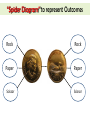
Probability (Unit 5)
•
•
Is the likelihood or chance of an even occurring.
Favourable Outcomes
Total Possible Outcomes
What is the probability of rolling the number 2 on a dice?
• How many favourable outcomes?
• How many possible outcomes?
• Place these numbers into the fraction
above…
How to express probability
•
Probability can be written in 3 ways...
•
As a fraction =
1/6
•
As a decimal =
0.16
•
As a percent
0.16 x 100% = 16%
How often will the
number 2 show up
when rolled?
Determine the probability
First you must find the possible outcomes (total) and then
the favourable outcomes (what you’re looking for). Then
place them into the probability equation.
Favourable Outcomes
Total Possible Outcomes
1.
2.
3.
4.
Rolling an even number on a dice?
Pulling a red card out from a deck of cards?
Using a four colored spinner to find green?
Selecting a girl from your class?
Determine the probability
A cookie jar contains 3 chocolate chip, 5 raisin, 11 Oreos,
and 6 almond cookies. Find the probability if you were to
reach inside the cookie jar for each of the cookies above.
Type of
Cookie
Fraction
Decimal
Percent
Ratio
Chocolate
Chip
Raisin
Oreo
Almond
Determine the probability
Page 163: # 3ab, 5, 7
Page 164: # 9
Organized Outcomes
Independent Events:
• The outcome of one event has not effect on the
outcome of another event
•
ROCK
Example:
PAPER
Tails
Head
SCISSOR
Organized Outcomes
Sample Space:
•
All possible outcomes of an experiment
Sample
Space
Head
Tail
Rock
Paper
Scissor
•
•
What is the probability of Paper/Head?
What is the probability of tails showing up?
“Tree Diagram” to represent Outcomes
Coin Flip
Rock,
Paper,
Scissor
H
R P S
T
R P S
H, Rock
H, Paper
H, Scissor
T, Rock
T, Paper
T, Scissor
Outcome
“Spider Diagram” to represent Outcomes
Rock
Rock
Paper
Paper
Scissor
Scissor
Organized Outcomes
You can find the sample space of two independent
events in many ways.
1. Chart
2. Tree Diagram
3. Spider Diagram
Your choice, but showing one of the above
illustrates that you can find the favourable and
possible outcomes for probability.
Organized Outcomes
Page 169: # 5, 8
Page 170: # 9, 10
Probabilities of Simple Independent Events
Random:
an event in which every outcome has an equal chance of
occurring.
A school gym has three doors on the stage and two back
doors. During a school play, each character enters through
one of the five doors. The next character to enter can be
either a boy or a girl. Use a “Tree Diagram” to determine
to show the sample space. Then answer the questions on
the next slide!
Probabilities of Simple Independent Events
Random:
an event in which every outcome has an equal chance of
occurring.
See Page 172 for your “Tree Diagram” of the school gym
doors!
Using a Table to DETERMINE Probabilities
How to determine probabilities:
Use “p” (or any other letter as the variable to represent
what you’re looking for) and divide it by “t” the total
outcomes. Then multiply your answer by 100%.
Equation stays the same:
p/t x 100%
Use your results from the “tree diagram” of the gym doors
and place them into a table. Then determine the
probabilities for the scenarios on the next slide!
Using a Table to DETERMINE Probabilities
How to determine probabilities:
p/t x 100%
Back Left
(BL)
Back Right
(BR)
Left Stage
(LS)
Centre
Stage (CS)
Right Stage
(RS)
Boy
BBL
BBR
BLS
BCS
BRS
Girl
GBL
GBR
GLS
GCS
GRS
Determine the probability for the scenarios below...
1. Of a boy using any right door?
2. Of anyone (boy or girl) using a stage door?
3. Of a girls using any of the doors?
Determine Probabilities
Page 175: # 6, 8
Page 176: # 13
Applications of Independent Events
Use Tree Diagrams, Charts or other graphic organizers to
solve probability problems.
How can you win at the game of “Sit & Save?”
RULES:
1.
2.
Stand up at the beginning of the round.
Two dice are rolled each round. You may collect the sum of
your dice as long as a “6” does NOT appear. A “6” means all
numbers before are cancelled and you get zero for that round.
3. After each roll you have two choices
•
Continue standing and roll again…hoping for no “6”
•
Sit and collect your total points!
Applications of Independent Events
How can you win at the game of “Sit & Save?”
Student
Names
1.
2.
3.
Round 1
Round 2
Round 3
Round 4
TOTAL
Who had the highest score?
What is the possibility of a 6 appearing with 2 dice? (sample data)
Use the numbers above for each player to find who had the
best probability (percent) of not rolling a 6.
Interpret Outcomes
Use Tree Diagrams, Charts or other graphic organizers to solve
probability problems.
1.
What are the 2 independent
events?
2.
What is the probability of
the sum of these 2 events
ending up to total “4”…
3.
What is the probability of
outcome having one 3
appear?
Interpret Outcomes
1.
What is the probability of red
appearing?
2.
What is the
possibility of a
black and green
appearing?
3.
What is the
possibility of both
events being two
syllable words
appearing?
Interpret Independent Outcomes
Page 181: # 6, 7
Page 182: # 9
Theoretical vs. Practical Probabilities
What are the chances of a boy and girl picking the same number
from 1-5. Try this 10 times and tally your results (Practical) . Then
compare to your “theoretical answer.”
Practical
Boy
Girl
Boy
Girl
Boy
Theoretical
Girl
1
2
3
4
5
Boy
B1
B2
B3
B4
B5
Girl
G1
G2
G3
G4
G5
Boy
Girl
Boy
Girl
Theoretical vs. Practical Probabilities
What are the chances of a boy and girl picking the same number
from 1-5. Try this 10 times and tally your results (practical) . Then
compare to your “theoretical” answer.
Practical
Boy
The probability of an event occurring based on
experimental results.
Girl
Boy
The expected probability of an event occurring.
Girl
Boy
Theoretical
Girl
1
2
3
4
5
Boy
B1
B2
B3
B4
B5
Girl
G1
G2
G3
G4
G5
Boy
Girl
Boy
Girl
Are your ready to be TESTED on “Probability?”
We have covered a lot of material in this unit. Do you have any
concerns or questions about any of the topics below?
1.
2.
3.
4.
5.
6.
7.
8.
Representing probability in different ways… (Pg. 158)
Types of sample spaces to find the probability (Pg. 166-167)
Explain how to identify an independent event.
Determine the outcomes of two independent events. (Pg. 172)
Find the sum of different events…which sample space would be best to use?
Solve multiple probabilities… P(1,B) or P(Girls, Boys, 6)
Use diagrams to interpret data and probabilities. (Pg. 178-179)
Compare experimental to theoretical probabilities. (Pg. 184)
If so, then you are ready for the test. For more practice and review of the test please
complete questions on page 190-191 (5, 8, 9, 12, and 13). Make sure to check your
answers to the back of the book so you are prepared for the exam. As well, if you have
any questions please see me in the morning or at lunch before the exam! For extra
practice complete the “Practice Test” on pages 192-193. Best of luck!