Download Lecture 8

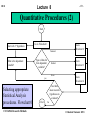
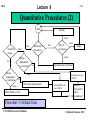
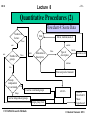
Lecture 8
HO 8
-1-
Quantitative Procedures (2)
Inferential Statistics:
Descriptive statistics deals with the analysis of data collected on
the sample (subjects). Inferential statistics is – in contrast –
concerned with what the subjects can tell us about the larger
population they represent.
It is usually impossible to observe the entire population of our
interest. We resort to observing and measuring the
characteristics of a sample of that population instead.
Example: To study the software defect discovery capability of
inspectors, we cannot observe everyone who has and will do
inspections. Instead we look at a sample population.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-2-
Quantitative Procedures (2)
The sample is selected and used as if it represents the general
population. Therefore, it better do so!
Strict sampling procedures must be followed. At any rate, due to
natural (chance) variability between any sample and its general
population, we CANNOT say, with certainty that any observation
made with respect to the sample would extend to the general
population. We can only talk about the probability that it would.
Example:
In a test designed to find the extent to which programmers with no
training in testing would find program defects compared to those
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-3-
Quantitative Procedures (2)
that have had such training, we find that the sample of
programmers under our study found on average 5.3 defects in
an hour of testing. The control group (the ones who were
trained in testing) found on average 5.8 defects.
What does this finding mean?
A. Given the difference between the sample groups, does this
mean that there is a difference between the trained
population and non-trained population?
B. Is this difference sufficiently significant to be 1) not just by
chance, 2) or small enough to not signify a real difference?
(so for example to recommend discontinuing tester training.)
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-4-
Quantitative Procedures (2)
Here, we are testing the null hypothesis that:
There is no real difference between the two population means.
We know about the null hypothesis and the type I and type II
errors. To go further, however, we need to distinguish between a
population parameter and a sample statistic.
A sample statistic is a statistic describing the sample drawn. For
example, taking the mean of the data-points from the sample.
A population parameter is a characteristic of the entire
population. For example if we take the mean of ALL data-points
in the population.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-5-
Quantitative Procedures (2)
Our task is usually to estimate population parameters and to draw
conclusions about population parameters based on sample
statistics.
Inferential statistics are used to compute the probability of
obtaining the observed data if the null-hypothesis were true. If
the probability is small, then it is unlikely that the nullhypothesis is true. The somewhat arbitrary cut-off points (called
alpha levels) were introduced to cater for such measure.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-6-
Quantitative Procedures (2)
Testing for mean differences:
Inferential statistics are used most frequently to evaluate mean
differences between groups. We can use such techniques to
specify the research hypothesis in terms of mean differences.
There are a number of tests for evaluating mean differences in two
or more groups. These include the:
1. Simple t-test
2. Correlated t-test
3. Analysis of Variance (ANOVA)
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-7-
Quantitative Procedures (2)
Simple t-test:
This test is typically used with score data from two independent
samples of subjects (e.g. trained and non-trained). The nullhypothesis is that there is NO difference in the two population
means. In other words , the observed difference between the
sample means is due only to chance. The test statistic is called
the t statistic. We compute the t statistic and the probability (p
value) of obtaining this t value if the null hypothesis is true. If p
is less than our alpha level, we reject the null-hypothesis and
conclude that the population means are different.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-8-
Quantitative Procedures (2)
We compute the t statistic using the following formula:
t
( X1  X 2 )
 SS1  SS2   1
1 




 N1  N 2  2   N1 N 2 
X1 and X 2 are the means of the two samples and SS 1
and SS 2 are the sum of squares of each sample.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
-9-
Quantitative Procedures (2)
Correlated t-test:
When we do not have independent samples, we use the
correlated t-test.
Examples of such design might be within-subject design, where
the same subjects appear in each group or matched-subjects
design, where all subjects are paired and then randomly
assigned so that one member of the pair goes into one group and
the other into another group.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 10 -
Quantitative Procedures (2)
An example of within-subject design might be when a group of
subjects are given an error free, a somewhat buggy and a bugriddled program to test. The testing time of each person testing
each program is recorded. As each subject is exposed to all
levels of the independent variable, the scores in each condition
are correlated with the scores in the other condition (i.e.
performance in one is correlated with performance in the other
condition.) The critical comparison is the difference between
correlated groups on the dependent variable (rate of defect
identification).
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 11 -
Quantitative Procedures (2)
An example of matched subject design would be when
comparing the effectiveness of training in two different
methods of testing software. If tester 1 is trained in method A
he or she cannot be trained in method B. We need a new
subject, say subject 2 who is the paired member of subject 1.
Now we can compare the two groups using a correlated t-test.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 12 -
Quantitative Procedures (2)
Analysis of Variance (ANOVA):
When we have more than two groups and want to test for
mutual mean difference between all the groups we usually use a
form of the ANOVA method. The term is actually confusing as
the test compares the means of the various groups but it does so
by computing and comparing the different population variance
estimates.
One advantage of ANOVA is that it allows analysis of one,two
or several independent variables at the same time. Each
independent variable is called a factor and the research design
with more than one factor is called factorial research design.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 13 -
Quantitative Procedures (2)
We refer to a study with only one independent variable as a oneway ANOVA, with two factors, it is called two-way ANOVA and
so forth.
Example: In a study of tester behavior it was found that testers do
generally better when there is a moderate level of other activity in
the work-place. Testing in total silence usually ends in poorer
result. Further investigation found that it is not the absence of
ambient noise that results in poor performance alone but that
conditions such as the mood of the tester, the load under which
they work, personal problems, etc. are also contributing factors. It
seems therefore that silence is a necessary but insufficient
condition for degradation of performance as are moods, problems
and loads. We can now set up a factorial design to test two or
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 14 -
Quantitative Procedures (2)
several independent variables may be considered. Let us say
we concentrate on two level of ambient noise (binary;
relatively noisy or silent) and mood (negative or positive). So
we have two factors and two levels for each. This gives four
treatment combinations leading to a 2 by 2 factorial design.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 15 -
Quantitative Procedures (2)
Multivariate Analysis of Variance (MANOVA):
The difference between MANOVA and ANOVA is in the
dependent variable. In ANOVA we can have multiple
independent variables but one dependent variable. In
MANOVA we can have multiple dependent variables also.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 16 -
Quantitative Procedures (2)
Mann-Whitney U test:
This is the comparison inferential test to be used if we have two
ordinal groups of data and the groups are independent.
Wilcoxon signed-rank test:
This is the comparison inferential test to be used if we have two
ordinal groups of data and the groups are not independent.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 17 -
Quantitative Procedures (2)
Kruskal-Wallis one-way ANOVA:
This is the comparison inferential test to be used if we have
more than two ordinal groups of data and the groups are
independent.
Friedman two-way ANOVA:
This is the comparison inferential test to be used if we have
more than two ordinal groups of data and the groups are not
independent.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 18 -
Quantitative Procedures (2)
Chi-square goodness of fit:
This is when we have one group being compare against a
hypothetical situation or a theory.
Chi-square test for independence:
This is when we have more than one group being compared
against each other.
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 19 -
Quantitative Procedures (2)
Start
Start with 1st hypothesis
Go to Flowchart 1
Go to
flowchart 2
Nominal
What is the dependent
variable?
Type of data for
that dependent
variable?
Ordinal
Score
yes
Selecting appropriate
Statistical Analysis
procedures. Flowchart 0
CSCI 6960- Research Methods
Go to
flowchart 3
Go to
flowchart 4
Are there
more research
hypotheses to
evaluate?
End
No
© Houman Younessi 2013
Lecture 8
HO 8
- 20 -
Quantitative Procedures (2)
Flowchart 1: Start-up
Start
Identify the following:
1.
Level of constraint (Naturalistic, case-study, correlational, …, experimental)
2.
Independent variables
3.
Levels and scale of independent variables
4.
Each independent variable manipulated or not.
5.
Type of design (independent groups, correlated groups, mixed..)
6.
Dependent variables
7.
Levels and scale of dependent variables
8.
Operational procedures
9.
Research hypothesis
10.
Type of test needed 9relationship or difference)
End
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 21 -
Quantitative Procedures (2)
Infer.
Start
Comparing one
group against
hypothetical
situation or two or
more groups
Inferential or
Descriptive
Frequency count
Desc.
one
Chi-square
goodness-of-fit
Two+
Chi-square test of
independence
Back to
flowchart 0.
More
hypotheses?
Flowchart 2: Nominal Data
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 22 -
Quantitative Procedures (2)
Start
Median
central
Infer.
Number of
groups
Three+
Groups
independent
or correlated
Two
Groups
independent
or correlated
Inferential or
Descriptive
Desc.
Type of
description
Range
relation
Corr..
Spearman rank correlation
Indep.
Freiedman two way
ANOVA
Corr.
Indep.
Variab.
Wilcoxon signed-rank test
Mann-Wittney U-test
Kruskal-Wallis one
way ANOVA
Back to
flowchart 0.
More
hypotheses?
Flowchart 3: Ordinal Data
CSCI 6960- Research Methods
© Houman Younessi 2013
Lecture 8
HO 8
- 23 -
Quantitative Procedures (2)
Flowchart 4: Score Data
Number of
factors
Start
Mean, median,mode,Z
Two+
one
one
central
Infer.
Number of
groups
Two+
Inferential or
Descriptive
Desc.
Type of
description
Variab.
Variance, std
relation
two
Pearson product moment
Groups
independent
or correlated
Indep.
Corr.
t test for correlated groups
t test for independent groups
Single group t test
CSCI 6960- Research Methods
ANOVA
Back to
flowchart 0.
More
hypotheses?
© Houman Younessi 2013