Download THERMOCHEMISTRY or Thermodynamics

Thermochemistry and Thermodynamics
1
Chemistry: The central Science AP version (10th edition, chapter 5)
Additional References and Resources
Powerpoint presentation from Melissa Brophy’s
website (modified for our needs)
Chemtour Animations and Vocab flashcards
from W.W. Norton site:
http://www.wwnorton.com/college/chemistry/gil
bert2/contents/ch05/studyplan.asp
(a) State functions and path functions (b) Internal
Energy (c) PV work (d) Calorimetry (e) Heating
Curves
POGILS:
Thermochemistry and Calorimetry
Hess’s Law: Enthalpy is a state function
Internal Energy and Enthalpy
Thermochemistry package: vocab, diagrams
and equations, practice problems (M.
Brophy)
© 2006 Brooks/Cole - Thomson
Lab experiments:
(1) Heat capacity of a metal
(2) Heat of neutralization (HCl + NaOH)
Activity (sign conventions for q and w) from
chap 5 online resources and movies (thermite;
AlBr3; NI3). Online practice quiz
Chemguy videos for introduction to energy and
thermochemistry or thermodynamics
http://www.youtube.com/watch?v=DIpGoOurt8&p=93017BDB7EDFE758&index=1&feature=
BF
Chem guy videos – thermodynamics 1-5 – one
video clip runs into the next one for more
advanced aspect of thermodynamics
For thermodynamics 1: spontaneous process,
enthalpy, entropy (system, surroundings,
universe)
http://www.youtube.com/watch?v=94p9ZfTjeKc
&p=2FDA79D443854B33&index=2&playnext=2
Chemistry and Chemical Reactivity
6th Edition
2
John C. Kotz
Paul M. Treichel
Gabriela C. Weaver
CHAPTER 6
Principles of Reactivity: Energy and Chemical Reactions
Lectures written by John Kotz
©2006
2006
Brooks/Cole
Thomson
©
Brooks/Cole
- Thomson
3
Thermodynamics and Thermochemistry
Thermodynamics
• Study of energy and its
transformations (or
Interconversions)
© 2006 Brooks/Cole - Thomson
Thermochemistry
• That part of
thermodynamics that
deals with the
relationships between
chemical reactions and
energy changes involving
heat
Energy & Chemistry
4
ENERGY is the capacity to do work or transfer heat.
work is the energy used to cause an object with mass
to move (w= F x d). When chemical reactions
involve gases, the work done may involve
compression or expansion of gases.
(w = -P∆V where P = pressure and ∆V = Vfinal-Vinitial)
heat is the form of energy that flows between 2
objects because of their difference in temperature.
Other forms of energy -Light, electrical, kinetic and
potential
© 2006 Brooks/Cole - Thomson
Internal Energy (E)
• PE + KE = Internal energy (E or U)
• Internal E of a chemical system
depends on
• number of particles
• type of particles
• temperature
© 2006 Brooks/Cole - Thomson
5
6
GO TO chemtours animation on
Internal Energy
• http://www.wwnorton.com/college/chemistry/
gilbert2/contents/ch05/studyplan.asp
© 2006 Brooks/Cole - Thomson
7
Changes in Internal Energy
• When a system undergoes any chemical or
physical change, the change in internal
energy is
•
∆E = q + w
[ ∆ E = Efinal- Einitial ]
• q = heat added or liberated from the system
• w = work done on or by the system
© 2006 Brooks/Cole - Thomson
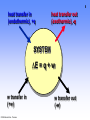
8
heat transfer in
(endothermic), +q
heat transfer out
(exothermic), -q
SYSTEM
∆E = q + w
w transfer in
(+w)
© 2006 Brooks/Cole - Thomson
w transfer out
(-w)
9
Go To TB animations and to
Chem Tours
• Activity (sign conventions for q and w) from
chap 5 online resources and movies
(thermite; AlBr3; NI3).
• (To Do as Homework)
• PV work from Chem tours:
• http://www.wwnorton.com/college/chemistry/
gilbert2/contents/ch05/studyplan.asp
© 2006 Brooks/Cole - Thomson
ENTHALPY
Most chemical reactions occur at constant P, so
Heat transferred at constant P = qp
qp =
∆H
where H
= enthalpy
and so ∆E = ∆H + w (and w is usually small)
∆H = heat transferred at constant P ≈ ∆E
∆H = change in heat content of the system
∆H = Hfinal – Hinitial
More on Enthalpy Later
© 2006 Brooks/Cole - Thomson
10
Internal Energy (E)
• Recall: PE + KE = Internal energy
(E or U)
• Internal E of a chemical system
depends on
• number of particles
• type of particles
• temperature
© 2006 Brooks/Cole - Thomson
11
Potential Energy
on the Atomic Scale
• Positive and
negative particles
(ions) attract one
another.
• Two atoms can
bond
• As the particles
attract they have a
lower potential
energy
© 2006 Brooks/Cole - Thomson
NaCl — composed of
Na+ and Cl- ions.
12
Potential Energy
on the Atomic Scale
• Positive and
negative particles
(ions) attract one
another.
• Two atoms can
bond
• As the particles
attract they have a
lower potential
energy
© 2006 Brooks/Cole - Thomson
+
13
_
14
Electrostatic potential energy
(Eel)
• Equation:
• The chemical energy associated with compounds is due to
the potential energy stored in the arrangement of atoms in a
substance (ex: bond energies)
© 2006 Brooks/Cole - Thomson
Potential & Kinetic Energy
Kinetic energy —
energy of
motion.
rotate
vibrate
translate
© 2006 Brooks/Cole - Thomson
15
Internal Energy (E)
• PE + KE = Internal energy (E or U)
© 2006 Brooks/Cole - Thomson
16
Internal Energy (E)
• The higher the T
the higher the
internal energy
• So, use changes
in T (∆T) to
monitor changes
in E (∆E).
© 2006 Brooks/Cole - Thomson
17
Thermodynamics
• Thermodynamics is the science of heat
(energy) transfer.
Heat energy is associated
with molecular motions.
Heat transfers until thermal equilibrium
is established.
∆T measures energy transferred.
© 2006 Brooks/Cole - Thomson
18
System and Surroundings
• SYSTEM
– The object under study
• SURROUNDINGS
– Everything outside the
system
© 2006 Brooks/Cole - Thomson
19
Heat
The flow of thermal energy from one
object to another.
Cup gets cooler while hand 20
gets warmer
Heat always flows from warmer to cooler
objects.
Ice gets warmer while
hand gets cooler
© 2006 Brooks/Cole - Thomson
Directionality of Heat Transfer
21
• Heat always transfer from hotter object to
cooler one.
• EXOthermic: heat transfers from SYSTEM
to SURROUNDINGS.
T(system) goes down
T(surr) goes up
© 2006 Brooks/Cole - Thomson
Directionality of Heat Transfer
• Heat always transfers from hotter object to
cooler one.
• ENDOthermic: heat transfers from
SURROUNDINGS to the SYSTEM.
T(system) goes up
T (surr) goes down
© 2006 Brooks/Cole - Thomson
22
23
Go To – chapter 5 – online
resources for our TB
• Go to Activity banner and view sign
conventions for q and w
• View movies (thermite; AlBr3; NI3)
• Write key points in margins of this page
• Reminder Online practice quiz for chapter 5
from our TB needs to be completed
© 2006 Brooks/Cole - Thomson
Energy & Chemistry
All of thermodynamics depends
on the law of
CONSERVATION OF ENERGY.
• The total energy is unchanged
in a chemical reaction.
• If PE of products is less than
reactants, the difference must
be released as KE.
© 2006 Brooks/Cole - Thomson
24
Energy Change in
Chemical Processes
PE
Reactants
Kinetic
Energy
Products
PE of system dropped. KE increased. Therefore,
you often feel a T increase.
© 2006 Brooks/Cole - Thomson
25
UNITS OF ENERGY
1 calorie = heat required to
raise temp. of 1.00 g of H2O
by 1.0 oC.
1000 cal = 1 kilocalorie = 1 kcal
1 kcal = 1 Calorie (a food
“calorie”)
But we use the unit called the
JOULE
1 cal = 4.184 joules
© 2006 Brooks/Cole - Thomson
James Joule
1818-1889
26
27
HEAT CAPACITY
The heat required to raise an
object’s T by 1 ˚C.
Which has the larger heat capacity?
© 2006 Brooks/Cole - Thomson
Specific Heat Capacity
How much energy is transferred
due to T difference?
The heat (q) “lost” or “gained” is
related to
a)
b)
sample mass
change in T and
c)
specific heat capacity
Specific heat capacity =
heat lost or gained by substance (J)
(mass, g)(T change, K)
© 2006 Brooks/Cole - Thomson
28
Specific Heat Capacity
Substance
Spec. Heat (J/g•K)
H2O
4.184
Ethylene glycol
2.39
Al
0.897
glass
0.84
Aluminum
© 2006 Brooks/Cole - Thomson
29
30
Specific Heat Capacity
If 25.0 g of Al cool
from 310 oC to 37 oC,
how many joules of
heat energy are lost
by the Al?
Specific heat capacity =
heat lost or gained by substance (J)
(mass, g)(T change, K)
© 2006 Brooks/Cole - Thomson
Specific Heat Capacity
If 25.0 g of Al cool from 310 oC to 37 oC, how many joules of
heat energy are lost by the Al?
heat gain/lose = q = (sp. ht.)(mass)(∆T)
where ∆T = Tfinal - Tinitial
q = (0.897 J/g•K)(25.0 g)(37 - 310)K
q = - 6120 J
Notice that the negative sign on q signals
heat “lost by” or transferred OUT of Al.
© 2006 Brooks/Cole - Thomson
31
Heat/Energy Transfer
No Change in State
q transferred = (sp. ht.)(mass)(∆T)
© 2006 Brooks/Cole - Thomson
32
Heat Transfer
• Use heat transfer as a way
to find specific heat
capacity, Cp
• 55.0 g Fe at 99.8 ˚C
• Drop into 225 g water at
21.0 ˚C
• Water and metal come to
23.1 ˚C
• What is the specific heat
capacity of the metal?
(Lab Activity)
© 2006 Brooks/Cole - Thomson
33
Heat Transfer
Because of conservation of energy,
q(Fe) = –q(H2O) (heat out of Fe = heat into H2O)
or q(Fe) + q(H2O) = 0
q(Fe) = (55.0 g)(Cp)(23.1 ˚C – 99.8 ˚C)
q(Fe) = –4219 • Cp
q(H2O) = (225 g)(4.184 J/K•g)(23.1 ˚C – 21.0 ˚C)
q(H2O) = 1977 J
q(Fe) + q(H2O) = –4219 Cp + 1977 = 0
Cp = 0.469 J/K•g
© 2006 Brooks/Cole - Thomson
34
Heat Transfer
with Change of State
Changes of state involve energy (at constant T)
Ice + 333 J/g (heat of fusion) -----> Liquid water
q = (heat of fusion)(mass)
© 2006 Brooks/Cole - Thomson
35
36
Heat Transfer and
Changes of State
Liquid ---> Vapor
Requires energy (heat).
This is the reason
a)
you cool down
after swimming
b)
you use water to
put out a fire.
© 2006 Brooks/Cole - Thomson
+ energy
37
GO TO chemtours animation on
Heating Curves
• http://www.wwnorton.com/college/chemistry/
gilbert2/contents/ch05/studyplan.asp
© 2006 Brooks/Cole - Thomson
Heating/Cooling Curve for Water
Note that T is
constant as ice melts
© 2006 Brooks/Cole - Thomson
38
Heat & Changes of State
What quantity of heat is required to melt
500. g of ice and heat the water to
steam at 100 oC?
Heat of fusion of ice = 333 J/g
Specific heat of water = 4.2 J/g•K
Heat of vaporization = 2260 J/g
+333 J/g
© 2006 Brooks/Cole - Thomson
+2260 J/g
39
Heat & Changes of State
What quantity of heat is required to melt 500. g of ice and
heat the water to steam at 100 oC?
1.
To melt ice
q = (500. g)(333 J/g) = 1.67 x 105 J
2.
To raise water from 0 oC to 100 oC
q = (500. g)(4.2 J/g•K)(100 - 0)K = 2.1 x 105 J
3.
To evaporate water at 100 oC
q = (500. g)(2260 J/g) = 1.13 x 106 J
4. Total heat energy = 1.51 x 106 J = 1510 kJ
© 2006 Brooks/Cole - Thomson
40
Chemical Reactivity
What drives chemical reactions? How do they
occur?
The first is answered by THERMODYNAMICS and
the second by KINETICS.
Have already seen a number of “driving forces”
for reactions that are PRODUCT-FAVORED.
• formation of a precipitate
• gas formation
• H2O formation (acid-base reaction)
• electron transfer in a battery
© 2006 Brooks/Cole - Thomson
41
Chemical Reactivity
But energy transfer also allows us to predict
reactivity.
In general, reactions that transfer energy
to their surroundings are productfavored.
So, let us consider heat transfer in chemical processes.
© 2006 Brooks/Cole - Thomson
42
Heat Energy Transfer in
a Physical Process
CO2 (s, -78 oC) ---> CO2 (g, -78 oC)
Heat transfers from surroundings to system in endothermic process.
© 2006 Brooks/Cole - Thomson
43
Heat Energy Transfer in a
Physical Process
• CO2 (s, -78 oC) ---> CO2
(g, -78 oC)
• A regular array of
molecules in a solid
-----> gas phase
molecules.
• Gas molecules have
higher kinetic energy.
© 2006 Brooks/Cole - Thomson
44
Energy Level Diagram
for Heat Energy
Transfer
CO2 gas
∆E = E(final) - E(initial)
= E(gas) - E(solid)
CO2 solid
© 2006 Brooks/Cole - Thomson
45
Heat Energy Transfer in
Physical Change
CO2 (s, -78 oC) ---> CO2 (g, -78 oC)
Two things have happened!
• Gas molecules have higher
kinetic energy.
• Also, WORK is done by the
system in pushing aside the
atmosphere.
© 2006 Brooks/Cole - Thomson
46
FIRST LAW OF
THERMODYNAMICS
heat energy transferred
∆E = q + w
energy
change
work done
by the
system
Energy is conserved!
© 2006 Brooks/Cole - Thomson
47
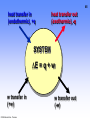
48
heat transfer in
(endothermic), +q
heat transfer out
(exothermic), -q
SYSTEM
∆E = q + w
w transfer in
(+w)
© 2006 Brooks/Cole - Thomson
w transfer out
(-w)
ENTHALPY
Most chemical reactions occur at constant P, so
Heat transferred at constant P = qp
qp =
∆H
where H
= enthalpy
and so ∆E = ∆H + w (and w is usually small)
∆H = heat transferred at constant P ≈ ∆E
∆H = change in heat content of the system
∆H = Hfinal - Hinitial
© 2006 Brooks/Cole - Thomson
49
ENTHALPY
∆H = Hfinal - Hinitial
If Hfinal > Hinitial then ∆H is positive
Process is ENDOTHERMIC
If Hfinal < Hinitial then ∆H is negative
Process is EXOTHERMIC
© 2006 Brooks/Cole - Thomson
50
USING ENTHALPY
Consider the formation of water
H2(g) + 1/2 O2(g) --> H2O(g) + 241.8 kJ
Exothermic reaction — heat is a “product”
and ∆H = – 241.8 kJ
© 2006 Brooks/Cole - Thomson
51
USING ENTHALPY
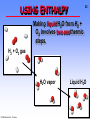
52
Making liquid H2O from H2 +
O2 involves two exothermic
steps.
H2 + O2 gas
H2O vapor
© 2006 Brooks/Cole - Thomson
Liquid H2O
USING ENTHALPY
Making H2O from H2 involves two steps.
H2(g) + 1/2 O2(g) ---> H2O(g) + 242 kJ
H2O(g) ---> H2O(liq) + 44 kJ
-----------------------------------------------------------------------
H2(g) + 1/2 O2(g) --> H2O(liq) + 286 kJ
Example of HESS’S LAW—
If a rxn. is the sum of 2 or more others,
the net ∆H is the sum of the ∆H’s of
the other rxns.
© 2006 Brooks/Cole - Thomson
53
54
ChemTours
GO TO:
http://www.wwnorton.com/college/che
mistry/gilbert2/contents/ch05/studyplan
.asp
View animation on
(a) State functions and path functions
Write key points on this page
© 2006 Brooks/Cole - Thomson
55
Hess’s Law
& Energy Level
Diagrams
Forming H2O can occur
in a single step or in a
two steps. ∆Htotal is the
same no matter which
path is followed.
Active Figure 6.18
© 2006 Brooks/Cole - Thomson
56
Hess’s Law
& Energy Level
Diagrams
Forming CO2 can occur
in a single step or in a
two steps. ∆Htotal is the
same no matter which
path is followed.
Active Figure 6.18
© 2006 Brooks/Cole - Thomson
57
∆H along one path =
∆H along another path
• This equation is valid because
∆H is a STATE FUNCTION
• These depend only on the state
of the system and not how it got
there.
• V, T, P, energy — and your bank
account!
• Unlike V, T, and P, one cannot
measure absolute H. Can only
measure ∆H.
© 2006 Brooks/Cole - Thomson
Standard Enthalpy Values
Most ∆H values are labeled ∆Ho
Measured under standard conditions
P = 1 atm = 101.3 kPa = 760 mmHg
Concentration = 1 mol/L
T = usually 25 oC
with all species in standard states
e.g., C = graphite and O2 = gas
© 2006 Brooks/Cole - Thomson
58
Enthalpy Values
Depend on how the reaction is written and on phases
of reactants and products
H2(g) + 1/2 O2(g) --> H2O(g)
∆H˚ = -242 kJ
2 H2(g) + O2(g) --> 2 H2O(g)
∆H˚ = -484 kJ
H2O(g) ---> H2(g) + 1/2 O2(g)
∆H˚ = +242 kJ
H2(g) + 1/2 O2(g) --> H2O(liquid)
© 2006 Brooks/Cole - Thomson
∆H˚ = -286 kJ
59
Standard Enthalpy Values
NIST (Nat’l Institute for Standards and
Technology) gives values of
∆Hfo = standard molar enthalpy of
formation
— the enthalpy change when 1 mol of
compound is formed from elements under
standard conditions.
See Table 5.3 and Appendix C of OUR TB and AP reference
Tables
© 2006 Brooks/Cole - Thomson
60
61
Reference Tables for
Thermochemistry
• Text Book: Table 5.3 Standard
enthalpies of formation and
Appendix C: Thermodynamic
Quantities for Selected
Substances at 298.15 K (25 °C)
Use these for problems from our
textbook.
• AP test reference tables
• Regents Reference tables
© 2006 Brooks/Cole - Thomson
∆Hfo, standard molar
enthalpy of formation
H2(g) + 1/2 O2(g) --> H2O(g)
∆Hfo (H2O, g)= -241.8 kJ/mol
By definition,
∆Hfo = 0 for elements in their
standard states.
© 2006 Brooks/Cole - Thomson
62
Using Standard Enthalpy Values
Use ∆H˚’s to calculate enthalpy change for
H2O(g) + C(graphite) --> H2(g) + CO(g)
(product is called “water gas”)
© 2006 Brooks/Cole - Thomson
63
Using Standard Enthalpy Values
H2O(g) + C(graphite) --> H2(g) + CO(g)
From reference books we find
• H2(g) + 1/2 O2(g) --> H2O(g)
∆Hf˚ of H2O vapor = - 242 kJ/mol
• C(s) + 1/2 O2(g) --> CO(g)
∆Hf˚ of CO = - 111 kJ/mol
© 2006 Brooks/Cole - Thomson
64
Using Standard Enthalpy Values
H2O(g) --> H2(g) + 1/2 O2(g) ∆Ho = +242 kJ
C(s) + 1/2 O2(g) --> CO(g) ∆Ho = -111 kJ
--------------------------------------------------------------------------------
H2O(g) + C(graphite) --> H2(g) + CO(g)
∆Honet = +131 kJ
To convert 1 mol of water to 1 mol each of H2
and CO requires 131 kJ of energy.
The “water gas” reaction is ENDOthermic.
© 2006 Brooks/Cole - Thomson
65
Using Standard Enthalpy Values
66
In general, when ALL
Calculate ∆H of
reaction?
enthalpies of formation are
known,
∆Horxn =
 ∆Hfo (products)
-  ∆Hfo (reactants)
Remember that ∆ always = final – initial
© 2006 Brooks/Cole - Thomson
Using Standard Enthalpy Values
Calculate the heat of combustion of
methanol, i.e., ∆Horxn for
CH3OH(g) + 3/2 O2(g) --> CO2(g) + 2 H2O(g)
∆Horxn =  ∆Hfo (prod) -  ∆Hfo (react)
© 2006 Brooks/Cole - Thomson
67
Using Standard Enthalpy Values
CH3OH(g) + 3/2 O2(g) --> CO2(g) + 2 H2O(g)
∆Horxn =  ∆Hfo (prod) -  ∆Hfo (react)
∆Horxn = ∆Hfo (CO2) + 2 ∆Hfo (H2O)
- {3/2 ∆Hfo (O2) + ∆Hfo (CH3OH)}
= (-393.5 kJ) + 2 (-241.8 kJ)
- {0 + (-201.5 kJ)}
∆Horxn = -675.6 kJ per mol of methanol
© 2006 Brooks/Cole - Thomson
68
69
Calorimetry
ChemTours
GO TO:
http://www.wwnorton.com/college/che
mistry/gilbert2/contents/ch05/studyplan
.asp
View animation on calorimetry and
Write key points in margins of this
page
© 2006 Brooks/Cole - Thomson
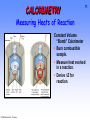
CALORIMETRY
Measuring Heats of Reaction
© 2006 Brooks/Cole - Thomson
70
CALORIMETRY
71
Measuring Heats of Reaction
Constant Volume
“Bomb” Calorimeter
• Burn combustible
sample.
• Measure heat evolved
in a reaction.
• Derive ∆E for
reaction.
© 2006 Brooks/Cole - Thomson
72
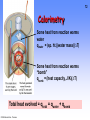
Calorimetry
Some heat from reaction warms
water
qwater = (sp. ht.)(water mass)(∆T)
Some heat from reaction warms
“bomb”
qbomb = (heat capacity, J/K)(∆T)
Total heat evolved = qtotal = qwater + qbomb
© 2006 Brooks/Cole - Thomson
Measuring Heats of Reaction
CALORIMETRY
Calculate heat of combustion of
octane.
C8H18 + 25/2 O2 -->
8 CO2 + 9 H2O
• Burn 1.00 g of octane
• Temp rises from 25.00 to 33.20 oC
• Calorimeter contains 1200 g water
• Heat capacity of bomb = 837 J/K
© 2006 Brooks/Cole - Thomson
73
Measuring Heats of Reaction
CALORIMETRY
Step 1
Calc. heat transferred from reaction to
water.
q = (4.184 J/g•K)(1200 g)(8.20 K) = 41,170 J
Step 2
Calc. heat transferred from reaction to
bomb.
q = (bomb heat capacity)(∆T)
= (837 J/K)(8.20 K) = 6860 J
Step 3
Total heat evolved
41,170 J + 6860 J = 48,030 J
Heat of combustion of 1.00 g of octane =
- 48.0 kJ
© 2006 Brooks/Cole - Thomson
74
Activities and Problem set 8
(due date_______)
TextBook ch. 5 – all sections required
for regents (in part), SAT II and AP
exams
•
Study (don’t write out) the sample
exercises
•
Do all in-chapter practice exercises
•
Do all GIST and Visualizing concepts
Vocab from Norton flash cards
Lab activities: (specific heat capacity
and heat of neutralization)
Ch 5 Problems TO DO: write out
questions and answers & show work
•
POGIL activities on Thermochemistry
and Calorimetry, Hess’s Law,
Internal Energy and Enthalpy
75
problems
•
Do end of chapter 5 exercises: 9,13, 18,
25, 28 , 29, 39, 40,42 , 43, 49, 51, 53, 54,
57, 60, 61, 63, 65, 67, 71 a,c, 74, 77, 85, 89,
Online practice quiz ch 5 due by_____
© 2006 Brooks/Cole - Thomson
90.