Download cuantica

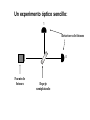
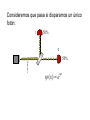
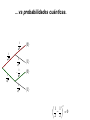
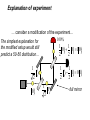
Richard Feynman: "El carácter de la ley física.
Computer technology is making
devices smaller and smaller…
…reaching a point where classical
physics is no longer a suitable
model for the laws of physics.
Physics and Computation
• Information is stored in a physical medium,
and manipulated by physical processes.
• The laws of physics dictate the capabilities of
any information processing device.
• Designs of “classical” computers are implicitly
based in the classical framework for physics
• Classical physics is known to be wrong or
incomplete… and has been replaced by a more
powerful framework: quantum mechanics.
The nineteenth century was known as the machine age, the twentieth
century will go down in history as the information age. I believe the twentyfirst century will be the quantum age. Paul Davies, Professor Natural
Philosophy – Australian Centre for Astrobiology
The design of devices on such a small scale will
require engineers to control quantum mechanical
effects.
Allowing computers to take advantage of
quantum mechanical behaviour allows us to do
more than cram increasingly many microscopic
components onto a silicon chip…
… it gives us a whole new framework in which
information can be processed in fundamentally
new ways.
Un experimento óptico sencillo:
1
Detectores de fotones
0
Fuente de
fotones
Espejo
semiplateado
Consideremos que pasa si disparamos un único
fotón:
1
50%
0
50%
Explicación simple: el espejo
semiplateado actúa como una moneda
clásica, de forma aleatoria manda cada
fotón a un detector u otro.
Consideremos una modificación del
experimento:
Desde el punto de vista
clásico esperaríamos que a
pesar de la modificación,
siguiéramos obteniendo
experimentalmente una
distribución 50-50…
1
100%
E1
0
E2
Espejo
normal
Pero eso no ocurre: siempre se detecta en el mismo detector.
Probabilidades clásicas
Calcularemos las probabilidades de que el fotón llegue a uno de los dos
detectores 0 o 1 a través de un árbol de posibilidades (los cuatro caminos
posibles).
1
2
E1
1
2
1
2
1
2
E2
1
2
0
1
0
1
1 1 1
 
2 2 4
1 1 1
 
2 2 4
1 1 1
 
2 2 4
1 1 1
P(0)   
4 4 2
1 1 1
 
2 2 4
P (1) 
1 1 1
 
4 4 2
…vs probabilidades cuánticas.
In quantum physics, we have probability amplitudes, which
can have complex phase factors associated with them.
1
2
1
2
1
2

|0
1
2
|1
1
2
|0
1
2
|1
The probability amplitude associated with a path
in the computation tree is obtained by multiplying
the probability amplitudes on that path. In the
example, the red path has amplitude 1/2, and the
green path has amplitude –1/2.
The probability amplitude for getting the answer |0
is obtained by adding the probability amplitudes…
notice that the phase factors can lead to
cancellations! The probability of obtaining |0 is
obtained by squaring the total probability
amplitude. In the example the probability of
getting |0 is
2
1 1
   0
2 2
Consideremos que pasa si disparamos un único
fotón:
1
50%
0
50%
 ( x)  e
i
…vs probabilidades cuánticas.
1
2
1
2
1
2

|0
1
2
|1
1
2
|0
1
2
|1
2
1 1
   0
2 2
Explanation of experiment
… consider a modification of the experiment…
100%
The simplest explanation for
1
1
the modified setup would still
0  0 1 0
predict a 50-50 distribution…
2
2
1
1
2
0
1
1
1  1  01
2
2
1
0
2
full mirror
When do we use which probability rules?
•If no path information is revealed, we must use
the quantum probability rules.
•If full path information is revealed, we must use
the classical probability rules.
•If partial path information is revealed, we must
use a combination of the two; i.e. there is a more
general set of rules that encapsulates both.
Quantum mechanics and information
Any physical medium capable of
representing 0 and 1 is in principle capable
of storing any linear combination 0 0  1 1
What does 0 0  1 1 really mean??
It’s a “mystery”. THE mystery. We don’t
understand it, but we can tell you how it works.
(Feynman)
The world of the quantum may be bizarre, but it is our world and our future.
Gerard Milburn, author of Schrödinger’s Machines.
Quantum mechanics and information
Any physical medium capable of
representing 0 and 1 is in principle capable
of storing any linear combination 0 0  1 1
How does this affect computational complexity?
How does this affect information security?
How does this affect communication complexity?
Would you believe a quantum proof?
How does quantum information help us better
understand physics?
How does this affect what is
feasibly computable?
Which “infeasible” computational tasks
become “feasible”?
How does this affect “computationally
secure” cryptography?
What new computationally secure
cryptosystems become possible?