Download Shell Structure of Nuclei and Cold Atomic Gases in Traps

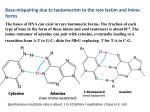
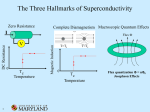
Shell Structure of Nuclei and Cold Atomic Gases in Traps
Sven Åberg, Lund University, Sweden
From Femtoscience to Nanoscience:
Nuclei, Quantum Dots, and Nanostructures
July 20 - August 28, 2009
Shell Structure of Nuclei and Cold Atomic Gases in Traps
I.
Shell structure from mean field picture
(a) Nuclear masses (ground-states)
(b) Ground-states in cold gas of Fermionic atoms: supershell structure
II. Shell structure of BCS pairing gap
(a) Nuclear pairing gap from odd-even mass difference
(b) Periodic-orbit description of pairing gap fluctuations
- role of regular/chaotic dynamics
(c) Applied to nuclear pairing gaps and to cold gases of Fermionic atoms
III. Cold atomic gases in a trap – Solved by exact diagonalizations
(a) Cold Fermionic atoms in 2D traps: Pairing versus Hund’s rule
(b) Effective-interaction approach to interacting bosons
Collaborators:
Stephanie Reimann, Massimo Rontani, Patricio Leboeuf
Henrik Olofsson/Urenholdt, Jeremi Armstrong, Matthias Brack,
Jonas Christensson, Christian Forssén, Magnus Ögren,
Marc Puig von Friesen, Yongle Yu,
I. Shell structure from mean field picture
I.a Shell structure in nuclear mass
Shell energy = Total energy (=mass) – Smoothly varying energy
Shell energy
P. Möller et al, At. Data and Nucl. Data Tables 59 (1995) 185
I.b Ground states of cold quantum gases
Trapped quantum gases of bosonic or fermionic atoms:
T0
Bose condensate
Degenerate fermi gas
Fermionic atoms in a 3D H.O. confinement
 pi2 m 2 2 
 2a N 3
H   
  ri   4
 (ri  rj )

2
m i j
i 1  2m

N
a = s-wave scattering length
Un-polarized two-component system with two spin-states:
n( r )  n  ( r )  n  ( r )  2n  ( r )
Hartree-Fock approximation:
 2
 
1
2 2

 
  m r  g  n (r )  i (r )  ei i (r )
2
 2m

Where:
N /2
n (r )    (r )

i 1
2

i
g  4 a / m
2
> 0 (repulsive int.)
N Fermionic atoms in harmonic trap – Repulsive int.
Shell energy: Eosc = Etot - Eav
Shell energy vs particle number for pure H.O.
No interaction
Fourier transform
Super-shell structure predicted for repulsive interaction[1]
g=0.2
g=0.4
g=2
Two close-lying frequencies
give rise to the beating pattern:
circle and diameter periodic orbits
2
4
Effective potential: Veff  1 2 eff r  1 4 r
[1] Y. Yu, M. Ögren, S. Åberg, S.M. Reimann, M. Brack, PRA 72, 051602 (2005)
II. Shell structure of BCS pairing gap [1]
[1] S. Åberg, H. Olofsson and P. Leboeuf, AIP Conf Proc Vol. 995 (2008) 173.
I. Odd-even mass difference
Extraction of pairing contribution from masses:
3 ( N )  B( N )  0.5B( N  1)  B( N  1)
 2 B 
1
2 3 ( N ) 


N 2 N g ( )
where
g (e) 

is s.p. level density
3(N even) =  + e/2
3(N odd) = 
If no pairing:
N=odd
dN
de
N=even
e
.
.
.
23(N) = 0

odd N
e
.
.
.
23(N) = e
W. Satula, J. Dobaczewski and W. Nazarewicz, PRL 81 (1998) 3599
even N
Odd-even mass difference from data
12/A1/2
3 (MeV)
even
odd+even
odd
2.7/A1/4
Single-particle distance from masses
Pairing delta eliminated in the difference:
(3)(even N) - (3)(odd N) = 0.5(en+1 – en) = d/2
50/A MeV
Fermi-gas model: 0.5(en1  en )  0.5  4eF / 3N  47 /A MeV
See e.g.: WA Friedman, GF Bertsch, EPJ A41 (2009) 109
Pairing gap 3odd from different mass models
Mass models all seem to provide pairing gaps in good agreement with exp.
P. Möller et al, At. Data and Nucl. Data Tables 59 (1995) 185.
M. Samyn et al, PRC70, 044309 (2004).
J. Duflo and A.P. Zuker, PRC52, R23 (1995).
Pairing gap from different mass models
Average behavior in agreement with exp. but very different fluctuations
Fluctuations of the pairing gap
II.b Periodic orbit description of BCS pairing Role of regular and chaotic dynamics
[1] H. Olofsson, S. Åberg and P. Leboeuf, Phys. Rev. Lett. 100, 037005 (2008)
Periodic orbit description of pairing
2
 (e)de
 
G  L e 2  2
L
Pairing gap equation:
Level density 
~ (e) 

 1 

  2 L exp  
 G 
   ~. Insert semiclassical expression

 Ap,r  cos(rS p /   p,r )
periodic r 1
orbits, p
Ap ,r : stability amplitude
Sp   pdq : action of periodic orbit p
 p,r : Maslov index
 p  S p / E : period of p.o
Divide pairing gap in smooth and fluctuating parts:
Expansion in fluctuating parts gives:
~
  

~
  2  Ap ,r K 0 (r p /   ) cosrS p (e) /   p ,r 

p ,r
where
h
 
2

is ”pairing time”
K 0 ( x)  
0
cos( xt)
1 t
2
dt  exp(  x) / x , x  1
Fluctuations of pairing gap
Fluctuations of pairing gap become
2 

~2
 2 2
H
 d K
2
o
( /   )K ( )
0
where K is the spectral form factor (Fourier transform of 2-point corr. function):
 min is shortest periodic orbit,  H  h  h / 
is Heisenberg time
~2
 /
RMS pairing fluctuations:  
If regular:
If chaotic:

2
reg

2
ch
 

F0 ( D)
4

1
2
2
F1 ( D)
Dimensionless ratio:
D=2R/0
(Number of Cooper pairs along 2R)
RMT-limit: D=0
: single-particle mean level spacing)
Size of system:
2R
Corr. length of Cooper pair: 0=vF/2
Bulk-limit: D→∞
Universal/non-universal fluctuations
D
 min 2 


g 
H
g
 min
”dimensionless conductance”
Non-universal spectrum fluctuations
for energy distances larger than g:
3 statistics
non-universal
universal
g=Lmax
Random matrix limit: g   (i.e. D = 0)
corresponding to pure GOE spectrum (chaotic)
or pure Poisson spectrum (regular)
~2
 /
RMS pairing fluctuations:  

If regular:
2
reg

If chaotic:
2
ch
 

F0 ( D)
4

1
2
2
F1 ( D)
Dimensionless ratio:
D=2R/0
(Number of Cooper pairs along 2R)
RMT-limit: D=0
Nuclei
Theory
(regular)
Exp.
: single-particle mean level spacing)
Size of system:
2R
Corr. length of Cooper pair: 0=vF/2
Bulk-limit: D→∞
Metallic grains
Irregular shape of grain 
chaotic dynamics
D very small (GOE-limit)
 ch2 
1
2 2
Universal pairing fluctuations
Fermionic atom gas
50 000 6Li atoms and kF|a| = 0.2

 1 0.24 , if regular


 1 0.02 , if chaotic

Fluctuations of nuclear pairing gap from mass models
Shell structure in nuclear pairing gap
Shell structure in nuclear pairing gap
Average over proton-numbers
Shell structure in nuclear pairing gap
Average over Z
P.O. description
III. Cold atomic gases in 2D traps
- Exact diagonalizations
III.a Cold Fermionic Atoms in 2D Traps [1]
N atoms of spin ½ and equal masses m confined in 2D harmonic trap,
interacting through a contact potential:
Energy scale: 0
Length scale:    / m0
Dimensionless coupling const.: g  g ' /( 0  2 )
Contact force regularized by energy cut-off [2].
Energy (and w.f.) of 2-body state relates strength g to scattering length a.
Solve many-body S.E. by full diagonalization
Ground-state energy and excitated states
obtained for all angular momenta
attractive
repulsive
[1] M. Rontani, JR Armstrong, Y, Yu, S. Åberg, SM Reimann, PRL 102 (2009) 060401.
[2] M. Rontani, S. Åberg, SM Reimann, arXiv:0810.4305
Attractive interaction
g=-0.3
Non-int
(g=0, pure HO)
Ground-state energy
E(N,g) in units of 
0
g=-3.0
g=-0.3
Interaction energy:
Eint(N,g) = E(N,g) – E(N,g=0)
-1
2
Scaled interaction energy:
Eint(N,g)/N3/2
10
18
g=-0.3
-0.015
-0.017
-0.019 2
10
18
Cold Fermionic Atoms in 2D Traps – Pairing versus Hund’s Rule
Interaction energy versus particle number
attractive
repulsive
Negative g (attractive interaction):
odd-even staggering (pairing)
Positive g (repulsive interaction):
Eint max at closed shells,
min at mid-shell (Hund’s rule)
Coulomb blockade – interaction blockade
Coulomb blockade:
Extra (electric) energy, EC, for a single electron to tunnel to a quantum dot with N electrons
Difference between conductance peaks:
 2 ( N )  E ( N  1)  2E ( N )  E ( N  1)  e  EC
where e is energy distance between s.p. states N and N+1 and E(N) total energy
Interaction (or van der Waals) blockade [1]:
Add an atom to a cold atomic gas in a trap
Attractive
interaction
Repulsive
interaction
No interaction
g=0.3
1.0
3.0
5.0 g=-0.3
-1.0
-3.0
-5.0

22
1
2
3
4
NN
5
6
Pairing
Cheinetgap:
et al,
PRL 101 (2008) 090404
3 ( N )  0.5 *  2 ( N )
7
[1] C. Capelle et al PRL 99 (2007) 010402
Angular momentum dependence – yrast line
E / 
E / 
Non-int. picture, N=2
3
Non-int. picture, N=8
3
M=1
M=2
M=0
2
1
-2
-1
0
1
2
m
M=0
M=2
M=1
2
1
-2
-1
0
1
2
m
Angular momentum dependence – 4 and 6 atoms
Yrast line – higher M-values, excited states
Pairing decreases with angular momentum
and excitation energy:

Gap to excited states decreases

”Moment of inertia” increases
Cold Fermionic Atoms in 2D Traps – 8 atoms
N=8 particles
Excitation spectra (6 lowest states for each M)
Attractive and repulsive interaction
Ground-state
attractive int.
Onset of intershell pairing
Excited states
almost deg.
with g.s.
(cf strongly corr. q. dot)
Ground-state
repulsive int.
Extracted pairing gaps
1st exc. state
N=4, N=8
3(3), 3(7)
-g/4 (pert. result)
Structure of w.f. from Conditional probability
Two fermions
g=0
fix ↓ fermion
measure probability
to find ↑ fermion in xy plane
Two fermions
g = - 0.1
Two fermions
g = - 0.3
Two fermions
g = - 0.6
Two fermions
g=-1
Two fermions
g = - 1.5
Two fermions
g=-2
Two fermions
g = - 2.5
Two fermions
g=-3
Two fermions
g = - 3.5
Two fermions
g=-4
Two fermions
g = - 4.5
Two fermions
g=-5
Two fermions
evolution of “Cooper pair”
formation in real space
g=-7
Conditional probability distr.
Repulsive
interaction
Attractive
interaction
III.b Effective interaction approach to the many-boson problem
N spin-less bosons confined in quasi-2D Harmonic-oscillator
Interact via (short-ranged) Gaussian interaction
Range: 
Strength: g
 

ri  rj
p
1
1
1

2 2 
H   
 m ri    g
exp  
2
2
2
2
2

2


i 1  2m
j

i


N
2
i
N
2




g → 0 implies interaction becomes -function
Form all properly symmetrized many-body
wave-functions (permanents) with energy:
Energy of non-interacting ground-state:
N max :
E   N  N max 
E  N
maximal energy of included states
Effective interaction approach to the many-boson problem
Effective interaction derived from Lee-Suzuki method
compared to
Exact diagonalization with same cut-off energy
N=9
L=0
g=1
g=10
L=9
g=10
Exact diagonalization
Effective interaction
N max
•Method works well for strong correlations
•Ground-state AND excited states
•All angular momenta
J. Christensson, Ch. Forssén, S. Åberg and S.M. Reimann, Phys Rev A 79, 012707 (2009)
Effective interaction approach to the many-boson problem
Not so useful for long-ranged interactions:
  0.1  /( m)
Energy
N=9 particles
L=0
g=10
Energy
  1.0  /( m)
N max
N max
SUMMARY
I.
Cold Fermionic gases show supershell structure in harmonic
confinement.
II. Fluctuations and shell structure of BCS gaps in nuclei well
described by periodic orbit theory. Non-universal corrections
to BCS fluctuations important (beyond RMT).
III. Cold Fermi-gas in 2D traps - Detailed shell structure:
Hund’s rule for repulsive int.; Pairing type for attractive int.
Pairing from: Odd-even energy difference, 1st excited state in
even-N system, Cond. prob. function
Interaction blockade. Yrast line spectrum
VI. Effective interaction scheme (Lee-Suzuki) works well for
many-body boson system (short-ranged force)