* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Quantum electrodynamics wikipedia , lookup
Quantum fiction wikipedia , lookup
Quantum decoherence wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
History of quantum field theory wikipedia , lookup
Probability amplitude wikipedia , lookup
Quantum computing wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum machine learning wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum entanglement wikipedia , lookup
Canonical quantization wikipedia , lookup
Quantum group wikipedia , lookup
Density matrix wikipedia , lookup
Hidden variable theory wikipedia , lookup
Quantum state wikipedia , lookup
Bell's theorem wikipedia , lookup
EPR paradox wikipedia , lookup
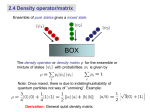
Quantum Teleportation and Bit Commitment Chi-Yee Cheung Chung Yuan Christian University June 9, 2009 What are teleportation and bit commitment? (1) Teleportation: Arguably the most novel of all quantum protocols (procedures). It allows one to recreate an unknown quantum state at a remote site without physically transferring the quantum state itself. (2) Bit commitment is a primitive (basic) two-party quantum protocol which can be use as the building block of other more complicated two-party protocols. Two parties Alice and Bob… What do these two protocols have in common? Before answering this question, I will have to tell you something about density matrix It is well know that for a pure state the density matrix is simply given by For a mixed state denoted by then Given a density matrix, there are always Infinitely many different representations, e.g., and etc. Purification: A mixed state in a Hilbert space can always be written as a pure state in a higher dimension Hilbert space Such that e.g., for the mixed state If party-A applies an unitary transformation on her states orthrononmal set namely, It is easy to show that the reduced density matrix on B’s side remain unchanged. *** It must be so, otherwise one could transfer information instantaneously! Theorem: All representations of can be generated in this manner. Hughston, Jozsa, and Wooters (Phys. Lett. A 183 (1993) 14.) This property of mixed quantum states has been found to be useful in discussions related to teleportation, bit commitment. Note that, although it is impossible for party-A (Alice) to remotely change the density matrix of party-B (Bob), it is nevertheless possible for her to change the representation of instantaneously at will! All she has to do is apply an appropriate transformation on the basis in her hand. (1) Teleportation Suppose Alice has an unknown quantum state , and in addition she shares a Bell (entangled) state with Bob: Then she can use this quantum channel to recreate at Bob’s site without sending the particle itself. It goes as follows: where and Therefore If Alice makes a “Bell measurement”, and tells Bob what she gets (say i=3 ), then Bob will be able to recreate in his lab. by making a compensating unitary transformation Note that: (1) The protocol is linear, that is, could be part of a N-particle state, so that one can teleport the whole N-particle state by repeating the above process N times. Provided, of course, Alice shares N pairs of Bell states with Bob, (2) could be a mixed state. Since as we have seen, any mixed state can be regarded as a pure state if one enlarges the Hilbert space. Question: What if the given quantum channel cannot be written as a product of Bell states? (i) How do we know if it could be used for teleportation? (ii) If so, how does one proceed? There exists no general result in the literature, and one just have to treat the problem on a case by case basis. For example, Zha and Song (Phys. Lett. A, 2007) considered the teleportation of a 2-particle state when the given channel is an arbitrary state (Alice: 1234; Bob: 56) They found that the combined state can always be recast in the form From which they conclude that if is unitary then Alice can teleport faithfully the 2-particle state. Otherwise, no. Also, Yeo and Chua (Phys. Rev. Lett. 96 (2006) 060502) found a class of so-called 4-particle genuinely entangled states which cannot be recast into a product of Bell states, but they can be used to teleport faithfully arbitrary 2-particle state. And there are others … 1. 2. 3. 4. 5. 6. P.X. Chen et al, PRA 74 (2006) 032324 J. Lee et al, PRA 66 (2002) 052318 G. Rigolin, PRA 71 (2005) 032303 P. Agrawal, PRA 74 (2006) 06232 S. Muralidharan et al, PRA 77 (2008) 032321 … However, all of the results are not general, in the sense that they work for some specifically constructed quantum channels only. . Note: (1) d is the number of unpolarized qubits in H_B (2) Local operations on H_B does not change the degree of entanglement between Alice and Bob. Conclusion: We have found a criterion which allows one to judge if any given quantum channel is good for faithful teleportation, and if so, how many qubits can it teleport. (2). Quantum bit commitment QBC is a quantum cryptographic protocol involving two parties: Alice and Bob They do not trust each other and they will do whatever it takes to gain an advantage! The security of QBC is an important issue because it can be used as the building block of various other twoparty quantum protocols, such as quantum coin tossing, etc. QBC: Commitment + Unveiling Commitment phase: • Alice secretly commits to a bit b = 0 or 1, which is to be revealed to Bob at a later time. • To ensure that Alice will not change her mind before unveiling, Alice and Bob execute a series of quantum and classical exchanges such that in the end, Bob has a quantum state in his hand. Unveiling phase: 1. Alice reveals the value of b. 2. With some additional information from Alice, Bob uses to check whether Alice is honest. Security issues: A QBC protocol is secure if it is 1. Binding: Alice cannot change her commitment without Bob’s knowledge. 2. Concealing: Bob cannot find out the value of b before Alice unveils it. Concealing condition implies: Ideal case Non-ideal case • Unconditional Security: If the protocol remains secure even when A and B had capabilities limited only by the laws of nature. (Security unaffected by any possible technological advances.) Example (1): 1. Alice writes b on a piece of paper and locks it in a box. 2. She gives the box (but not the key) to Bob as evidence of her commitment. Concealing: Bob cannot read the paper Binding: Paper is in Bob’s hand However classical BC cannot be unconditionally secure, because it’s security is always dependent on some unproven assumptions: (1) The box is hard to break (2) Bob cannot pick the lock (3) Etc…. How about QBC? Example (2): To commit, Alice sends Bob a sequence of qubits Where Concealing: Binding: If Alice commits to b=0 initially, she cannot open as b=1, for if she did, her chance of success on each qubit is ½, therefore the overall chance of cheating successfully is exponentially small. So naively, it seems that such a protocol is unconditionally secure! •No-Go Theorem Lo and Chau (1997), Mayers (1997) If a protocol is concealing, it cannot be binding at the same time. Unconditionally secure QBC is impossible as a matter of principle. Main Idea of the Proof: Purification – Alice leaves all undisclosed classical information undetermined at the quantum level by entangling with ancillas. • Any action taken on a quantum system can be represented by an unitary transformation on system + environment (ancillas) • Needs quantum computers. Purification At the end of commitment phase: • Instead of a mixed state in • There exists a pure state in • HA is used to store Alice’s undisclosed info. As long as Bob cannot tell whether Alice purifies or not! Then Alice has a perfect cheating strategy (EPR attack): Because Hence, Notice: UA acts on HA only Alice can execute it without Bob’s knowledge Therefore Alice can unveil b=0 or b=1 at will. Cheating! (That is, the protocol is not binding!) How does it work in example (2)? Instead of honestly producing She generates That is, instead of fixing undisclosed information at the beginning, Alice leaves it undetermined at the quantum level. That is, recorded in ancillary qubit states. Then she can cheat perfectly: So it seems that unconditionally secure QBC is impossible! Question: Does the “no-go theorem” cover all possible cases? Note that QBC has a definite objective, but the corresponding procedure is not precisely defined. There are infinitely many ways to do QBC. So how could one be sure the no-go result is universally valid? * Secret Parameters In the impossibility proof, in order that Alice knows UA, it is assumed that Alice knows every details of the protocol, so that no secret parameters exist. What if Bob is allowed to generate secret parameters unknown to Alice? The point is: If the pure state depends on some parameter unknown to Alice? Then 1. In general, depends on 2. But is not known to Alice, therefore she cannot calculate 3. If so, then unconditionally secure QBC might be possible (?) The point is, the no-go theorem only proves the existence of , but there is no guarantee that it is known to Alice! However, we find that for a concealing QBC protocol, the cheating unitary transformation is independent of any secret parameter (probability distribution), , chosen by Bob. (Purification is assumed to hold. In a purified approach, probability distributions are the only possible unknowns left.) Proof: If Bob is allowed to choose from in secret, then he can purify his choices with an associated probability distribution That is, instead of picking a particular , Bob entangles all his possible choices Where are orthonormal ancilla states. Now the protocol is concealing. Therefore no matter what Bob uses, the resulting reduced density matrix must be independent of b Then there exists an that Since Whereas such `s are orthogonal states in acts on HA only. Then it is easy to show that Hence Is independent of ! Hence we have proved that Alice can cheat perfectly whether Bob uses secret parameters or not. *Conclusion For a concealing QBC protocol, i.e., is independent of any of Bob’s secret choices, and Alice can calculate it without knowing them. Therefore, even if Bob is allowed to generate secret parameters unknown to Alice, she can still cheat perfectly. Our result enlarges the applicability of the no-go theorem to include cases where the parties are allowed to use parameters not known to each other. Thank you! • Lo and Chau: “In order that Alice and Bob can follow the procedures, they must know the exact forms of all unitary transformations involved“ • Mayers: “It is a principle that we must assume that every participant knows every detail of the protocol, including the distribution of probability of a random variable generated by another participant"