Download Slide 1

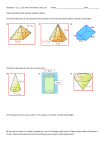
Geometry B
Section 12.3
Surface Area of Pyramids and Cones
A pyramid is a polyhedron in which the base is a polygon and the lateral
faces are triangles with a common vertex.
The intersection of two lateral faces is a lateral edge.
The intersection of a lateral face and the base is the
base edge.
A regular pyramid has a regular polygon for its base and the vertex is
straight above the center of the base.
This pyramid is not
regular.
The slant height of a regular pyramid
is the distance from the vertex to the
center of a base edge.
The height or altitude of a regular pyramid is the distance from the vertex to the center
of the base.
The slant height of a regular pyramid is the distance
from the vertex to the center of a base edge.
Theorem 12.4 Surface Area of a Regular Pyramid
The surface area, S, of a regular pyramid is S = B + ½PL, where B is
the area of the base, P is the perimeter of the base and L is the slant
height.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A cone is a solid that has a circular base and a vertex that is not in the
same plane as the base. The lateral surface consists of all segments
that connect the vertex to points on the circle.
A right cone is one in which the vertex is right above the center of the base.
This cone is not right.
The slant height of a right cone is the distance between the vertex and
a point on the edge of the base.
Theorem 12.5 Surface Area of a Right Cone
The surface area of a right cone, S, is S = πr2 + πrL where r is the
radius of the base and L is the slant height.