Download Integrative Studies 410 Our Place in the Universe

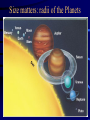
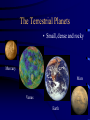
From Newton to Einstein
• If we use Newton II and the law of universal
gravity, we can calculate how a celestial object
moves, i.e. figure out its acceleration, which leads
to its velocity, which leads to its position as a
function of time:
ma= F = GMm/r2
so its acceleration a= GM/r2 is independent of its mass!
• This prompted Einstein to formulate his
gravitational theory as pure geometry.
Orbital Motion
Cannon “Thought Experiment”
• http://www.phys.virginia.edu/classes/109N/more_stuff/Appl
ets/newt/newtmtn.html
Applications
• From the distance r between two bodies and the
gravitational acceleration a of one of the bodies,
we can compute the mass M of the other
F = ma = G Mm/r2 (m cancels out)
– From the weight of objects (i.e., the force of gravity)
near the surface of the Earth, and known radius of Earth
RE = 6.4103 km, we find ME = 61024 kg
– Your weight on another planet is F = m  GM/r2
• E.g., on the Moon your weight would be 1/6 of what it is on
Earth
Applications (cont’d)
• The mass of the Sun can be deduced from the
orbital velocity of the planets: MS = rOrbitvOrbit2/G
= 21030 kg
– actually, Sun and planets orbit their common center of
mass
• Orbital mechanics. A body in an elliptical orbit
cannot escape the mass it's orbiting unless
something increases its velocity to a certain value
called the escape velocity
– Escape velocity from Earth's surface is about 25,000
mph (7 mi/sec)
The Solar System
Contents of the Solar System
• Sun
• Planets – 9 known (now: 8)
– Mercury, Venus, Earth, Mars (“Terrestrials”)
– Jupiter, Saturn, Uranus, Neptune (“Jovians”)
– Pluto (a Kuiper Belt object?)
• Natural satellites (moons) – over a hundred
• Asteroids and Meteoroids
– 6 known that are larger than 300 km across
– Largest, Ceres, is about 940 km in diameter
• Comets
• Rings
• Dust
Size matters: radii of the Planets
The Astronomical Unit
• A convenient unit of length for discussing
the solar system is the Astronomical Unit
(A.U.)
• One A.U. is the average distance between
the Earth and Sun
– About 1.5  108 km or 8 light-minutes
• Entire solar system is about 80 A.U. across
The Terrestrial Planets
• Small, dense and rocky
Mercury
Mars
Venus
Earth
The Jovian Planets
• Large, made out of gas, and low density
Saturn
Jupiter
Uranus
Neptune
Asteroids, Comets and
Meteors
Debris in the Solar System
Asteroids
Asteroid Discovery
• First (and largest) Asteroid Ceres
discovered New Year’s 1801 by G. Piazzi,
fitting exactly into Bode’s law: a=2.8 A.U.
• Today more than 100,000 asteroids known
• Largest diameter 960 km, smallest: few km
• Most of them are named
• about 20 of them are visible with binoculars
How bright does a planet, moon,
asteroid or comet appear?
• Apparent brightness of objects that reflect
sunlight do depends on three things:
– Size of the object (the bigger the brighter)
– Distance to the object (the closer the brighter)
– “Surface” properties of the object (the whiter the
brighter, the darker the dimmer)
• Technical term: Albedo (Albedo =1.00 means 100% of
incoming radiation is reflected)
Comets - Traveling Dirty Snowballs
• Small icy bodies, “dirty snowballs”
• Develops a “tail” as it approaches the Sun
Comet Anatomy
• Tail may be up to 1 A.U. long
Comet Tail
• Two kinds of tails:
• Dust
• Ion (charged
particles)
Shapes
Comet GiacobiniZinner (1959)
• Ion tail 500,000 km long
• Coma: 70,000 km across
Comet Hale-Bopp
(1997)
• Tail 40° long as seen
from earth
Short- and Long-Period Comets
• “Short” period meaning: less than 200 years
Halley’s Comet – a typical Comet
Halley’s Comet – Now and then
• Halley’s Comet in 1910
• Top: May 10, 30° tail
• Bottom May 12, 40° tail
• Halley’s Comet in 1986
• March 14, 1986