Download (a) (i) Define electromotive force (emf ) of a battery. (1 mark) (ii

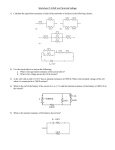
(a)
(i) Define electromotive force (emf ) of a battery.
(ii) Define electrical resistance of a conductor.
(1 mark)
(1 mark)
(b)
A battery of emf ε and negligible internal resistance
is connected in series to two resistors.
The current in the circuit is I.
(i)
State an equation giving the total power delivered
by the battery. (1 mark)
(ii)
The potential difference across resistor R1 is V1 and that across resistor R2 is V2.
Using the law of the conservation of energy, deduce the equation below.
ε = V1 + V2
(2 marks)
(c)
The graph shows the I-V characteristics of two conductors, X and Y.
On the axes below, sketch graphs to show the variation with potential difference V of the resistance
of conductor X (label this graph X) and conductor Y (label this graph Y).
You do not need to put any numbers on the vertical axis.
(3marks)
(d)
The conductors in (c) are connected in series
to a battery of emf ε and negligible internal
resistance.
The power dissipated in each of the two resistors
is the same.
Using the graph given in (c),
(i)
determine the emf of the battery.
(ii)
calculate the total power dissipated in the circuit.
(2 marks)
(2 marks)
(a) (i) the work done per unit charge in moving a quantity of charge completely
around a circuit / the power delivered per unit current / work done per unit
charge made available by a source; [1]
(ii) the ratio of the voltage across to the current in the conductor; [1]
(b) (i) emf × current; [1]
(ii) total power is V1I +V2I;
equating with EI to get result;
or
total energy delivered by battery is EQ;
equate with energy in each resistor V1 Q +V2 Q; [2]
(c) graph X: horizontal straight line;
graph Y: starts lower than graph X;
rises (as straight line or curve) and intersects at 4.0 V; [3]
Do not pay attention to numbers on the vertical axis.
(d) (i) realization that the voltage must be 4.0 V across each resistor;
and so emf is 8.0 V; [2]
(ii) power in each resistor = 3.2W;
Or
current is 0.80 A;
and so total power is 6.4 W;
so total power is 8.0×0.80 = 6.4W; [2]