Download Learning with Perceptrons and Neural Networks

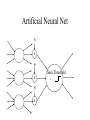
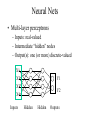
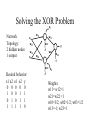
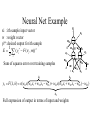
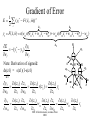
Learning with Perceptrons
and Neural Networks
Artificial Intelligence
CMSC 25000
February 14, 2002
Agenda
• Neural Networks:
– Biological analogy
• Perceptrons: Single layer networks
• Perceptron training: Perceptron convergence theorem
• Perceptron limitations
• Neural Networks: Multilayer perceptrons
• Neural net training: Backpropagation
• Strengths & Limitations
• Conclusions
Neurons: The Concept
Dendrites
Axon
Nucleus
Cell Body
Neurons: Receive inputs from other neurons (via synapses)
When input exceeds threshold, “fires”
Sends output along axon to other neurons
Brain: 10^11 neurons, 10^16 synapses
Artificial Neural Nets
• Simulated Neuron:
– Node connected to other nodes via links
• Links = axon+synapse+link
• Links associated with weight (like synapse)
– Multiplied by output of node
– Node combines input via activation function
• E.g. sum of weighted inputs passed thru threshold
• Simpler than real neuronal processes
Artificial Neural Net
w
x
w
x
w
x
Sum Threshold
+
Perceptrons
• Single neuron-like element
– Binary inputs
– Binary outputs
• Weighted sum of inputs > threshold
– (Possibly logic box between inputs and weights)
Perceptron Structure
y
w0
w1
x0=-1
x1
wn
w2
x2
w3
x3
. . .
n

1 if  wi xi  0
y
i 0
0 otherwise

x0 w 0
compensates for threshold
xn
Perceptron Convergence Procedure
• Straight-forward training procedure
– Learns linearly separable functions
• Until perceptron yields correct output for all
– If the perceptron is correct, do nothing
– If the percepton is wrong,
• If it incorrectly says “yes”,
– Subtract input vector from weight vector
• Otherwise, add input vector to weight vector
Perceptron Convergence Example
• LOGICAL-OR:
•
•
•
•
•
Sample
1
2
3
4
x1
0
0
1
1
x2
0
1
0
1
x3
1
1
1
1
Desired Output
0
1
1
1
• Initial: w=(0 0 0);After S2, w=w+s2=(0 1 1)
• Pass2: S1:w=w-s1=(0 1 0);S3:w=w+s3=(1 1 1)
• Pass3: S1:w=w-s1=(1 1 0)
Perceptron Convergence Theorem
n

1 if  wi xi  0
y
i 0
0 otherwise

• If there exists a vector W s.t.
• Perceptron training will find it
• Assume v.x > 
for all +ive examples x
• w=x1+x2+..xk, v.w>= k 
• |w|^2 increases by at most 1, in each iteration
• |w+x|^2 <= |w|^2+1…..|w|^2 <=k (# mislabel)
• v.w/|w| > k  / k <= 1
Converges in k <= (1/  )^2 steps
Perceptron Learning
• Perceptrons learn linear decision boundaries
x2
x2
0 0
• E.g.
+ +
+
+ ++
0
0 0
But not
+
0
0
x1
X1 X2
-1
-1
1
-1
1
1
-1
1
0
+
0
xor
x1
w1x1 + w2x2 < 0
w1x1 + w2x2 > 0 => implies w1 > 0
w1x1 + w2x2 >0 => but should be false
w1x1 + w2x2 > 0 => implies w2 > 0
Neural Nets
• Multi-layer perceptrons
– Inputs: real-valued
– Intermediate “hidden” nodes
– Output(s): one (or more) discrete-valued
X1
Y1
X2
X3
Y2
X4
Inputs
Hidden
Hidden
Outputs
Neural Nets
• Pro: More general than perceptrons
– Not restricted to linear discriminants
– Multiple outputs: one classification each
• Con: No simple, guaranteed training
procedure
– Use greedy, hill-climbing procedure to train
– “Gradient descent”, “Backpropagation”
Solving the XOR Problem
o1
Network
Topology:
2 hidden nodes
1 output
Desired behavior:
x1 x2 o1 o2 y
0 0 0 0 0
1 0 0 1 1
0 1 0 1 1
1 1 1 1 0
x1
w11
w01
w21
-1
w12
x2
w13
y
w23
w22
w03
-1
w02 o
2
-1
Weights:
w11= w12=1
w21=w22 = 1
w01=3/2; w02=1/2; w03=1/2
w13=-1; w23=1
Backpropagation
• Greedy, Hill-climbing procedure
– Weights are parameters to change
– Original hill-climb changes one parameter/step
• Slow
– If smooth function, change all parameters/step
• Gradient descent
– Backpropagation: Computes current output, works
backward to correct error
Producing a Smooth Function
• Key problem:
– Pure step threshold is discontinuous
• Not differentiable
• Solution:
– Sigmoid (squashed ‘s’ function): Logistic fn
n
1
z   wi xi s ( z ) 
z
1

e
i
Neural Net Training
• Goal:
– Determine how to change weights to get correct
output
• Large change in weight to produce large reduction
in error
• Approach:
•
•
•
•
Compute actual output: o
Compare to desired output: d
Determine effect of each weight w on error = d-o
Adjust weights
Neural Net Example
y3
xi : ith sample input vector
w : weight vector
yi*: desired output for ith sample
E
z3
w03
1
  2
*
(
y

F
(
x

i
i , w))
2 i
-1
z1
Sum of squares error over training samples
w13 y1 w23 y2
z2
w21
w01
-1
w1
1
z1
z2
x1
w12
w22
x2
w02
-1
 
y3  F ( x, w)  s(w13s(w11x1  w21x2  w01 )  w23s(w12 x1  w22 x2  w02 )  w03 )
z3
Full expression of output in terms of input and weights
Gradient Descent
• Error: Sum of squares error of inputs with
current weights
• Compute rate of change of error wrt each
weight
– Which weights have greatest effect on error?
– Effectively, partial derivatives of error wrt weights
• In turn, depend on other weights => chain rule
Gradient
of
Error
 
1
E   ( yi*  F ( xi , w)) 2
2 i
z1
z2
 
y3  F ( x, w)  s(w13s(w11x1  w21x2  w01 )  w23s(w12 x1  w22 x2  w02 )  w03 )
y3
E
*
 ( yi  y3 )
w j
w j
y3
z3
z3
w03
Note: Derivative of sigmoid:
ds(z1) = s(z1)(1-s(z1)
z1
y3 s( z3 ) z3 s( z3 )
s ( z3 )


s( z1 ) 
y1
w13
z3 w13
z3
z3
-1
z1
w13 y1 w23 y2
z2
w21
w01
-1
w1
1
x1
w12
w22
x2
y3 s ( z3 ) z3 s ( z3 )
s ( z1 ) z1 s( z3 )
s ( z1 )


w13

w13
x1
w11
z3 w11
z3
z1 w11
z3
z1
MIT AI lecture notes, Lozano-Perez
2000
w02
-1
From Effect to Update
• Gradient computation:
– How each weight contributes to performance
• To train:
– Need to determine how to CHANGE weight
based on contribution to performance
– Need to determine how MUCH change to make
per iteration
• Rate parameter ‘r’
– Large enough to learn quickly
– Small enough reach but not overshoot target values
Backpropagation Procedure
i
wi  j
w j k
j
k
oj
oi
• Pick rate parameter ‘r’
o (1  o )
• Until performance is good enough,
j
j
ok (1  ok )
– Do forward computation to calculate output
– Compute Beta in output node with
 z  d z  oz
– Compute Beta in all other nodes with
 j   w j k ok (1  ok )  k
k
– Compute change for all weights with
wi  j  ro j (1  o j )  j
Backpropagation Observations
• Procedure is (relatively) efficient
– All computations are local
• Use inputs and outputs of current node
• What is “good enough”?
– Rarely reach target (0 or 1) outputs
• Typically, train until within 0.1 of target
Neural Net Summary
• Training:
– Backpropagation procedure
• Gradient descent strategy (usual problems)
• Prediction:
– Compute outputs based on input vector & weights
• Pros: Very general, Fast prediction
• Cons: Training can be VERY slow (1000’s of
epochs), Overfitting
Training Strategies
• Online training:
– Update weights after each sample
• Offline (batch training):
– Compute error over all samples
• Then update weights
• Online training “noisy”
– Sensitive to individual instances
– However, may escape local minima
Training Strategy
• To avoid overfitting:
– Split data into: training, validation, & test
• Also, avoid excess weights (less than # samples)
• Initialize with small random weights
– Small changes have noticeable effect
• Use offline training
– Until validation set minimum
• Evaluate on test set
– No more weight changes
Classification
• Neural networks best for classification task
– Single output -> Binary classifier
– Multiple outputs -> Multiway classification
• Applied successfully to learning pronunciation
– Sigmoid pushes to binary classification
• Not good for regression
Neural Net Conclusions
• Simulation based on neurons in brain
• Perceptrons (single neuron)
– Guaranteed to find linear discriminant
• IF one exists -> problem XOR
• Neural nets (Multi-layer perceptrons)
– Very general
– Backpropagation training procedure
• Gradient descent - local min, overfitting issues