* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Learning with Perceptrons and Neural Networks
Neural modeling fields wikipedia , lookup
Cross-validation (statistics) wikipedia , lookup
Perceptual control theory wikipedia , lookup
Gene expression programming wikipedia , lookup
Pattern recognition wikipedia , lookup
Hierarchical temporal memory wikipedia , lookup
Backpropagation wikipedia , lookup
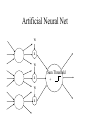
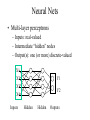
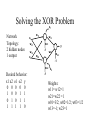
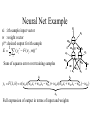
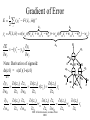
Learning with Perceptrons and Neural Networks Artificial Intelligence CMSC 25000 February 14, 2002 Agenda • Neural Networks: – Biological analogy • Perceptrons: Single layer networks • Perceptron training: Perceptron convergence theorem • Perceptron limitations • Neural Networks: Multilayer perceptrons • Neural net training: Backpropagation • Strengths & Limitations • Conclusions Neurons: The Concept Dendrites Axon Nucleus Cell Body Neurons: Receive inputs from other neurons (via synapses) When input exceeds threshold, “fires” Sends output along axon to other neurons Brain: 10^11 neurons, 10^16 synapses Artificial Neural Nets • Simulated Neuron: – Node connected to other nodes via links • Links = axon+synapse+link • Links associated with weight (like synapse) – Multiplied by output of node – Node combines input via activation function • E.g. sum of weighted inputs passed thru threshold • Simpler than real neuronal processes Artificial Neural Net w x w x w x Sum Threshold + Perceptrons • Single neuron-like element – Binary inputs – Binary outputs • Weighted sum of inputs > threshold – (Possibly logic box between inputs and weights) Perceptron Structure y w0 w1 x0=-1 x1 wn w2 x2 w3 x3 . . . n 1 if wi xi 0 y i 0 0 otherwise x0 w 0 compensates for threshold xn Perceptron Convergence Procedure • Straight-forward training procedure – Learns linearly separable functions • Until perceptron yields correct output for all – If the perceptron is correct, do nothing – If the percepton is wrong, • If it incorrectly says “yes”, – Subtract input vector from weight vector • Otherwise, add input vector to weight vector Perceptron Convergence Example • LOGICAL-OR: • • • • • Sample 1 2 3 4 x1 0 0 1 1 x2 0 1 0 1 x3 1 1 1 1 Desired Output 0 1 1 1 • Initial: w=(0 0 0);After S2, w=w+s2=(0 1 1) • Pass2: S1:w=w-s1=(0 1 0);S3:w=w+s3=(1 1 1) • Pass3: S1:w=w-s1=(1 1 0) Perceptron Convergence Theorem n 1 if wi xi 0 y i 0 0 otherwise • If there exists a vector W s.t. • Perceptron training will find it • Assume v.x > for all +ive examples x • w=x1+x2+..xk, v.w>= k • |w|^2 increases by at most 1, in each iteration • |w+x|^2 <= |w|^2+1…..|w|^2 <=k (# mislabel) • v.w/|w| > k / k <= 1 Converges in k <= (1/ )^2 steps Perceptron Learning • Perceptrons learn linear decision boundaries x2 x2 0 0 • E.g. + + + + ++ 0 0 0 But not + 0 0 x1 X1 X2 -1 -1 1 -1 1 1 -1 1 0 + 0 xor x1 w1x1 + w2x2 < 0 w1x1 + w2x2 > 0 => implies w1 > 0 w1x1 + w2x2 >0 => but should be false w1x1 + w2x2 > 0 => implies w2 > 0 Neural Nets • Multi-layer perceptrons – Inputs: real-valued – Intermediate “hidden” nodes – Output(s): one (or more) discrete-valued X1 Y1 X2 X3 Y2 X4 Inputs Hidden Hidden Outputs Neural Nets • Pro: More general than perceptrons – Not restricted to linear discriminants – Multiple outputs: one classification each • Con: No simple, guaranteed training procedure – Use greedy, hill-climbing procedure to train – “Gradient descent”, “Backpropagation” Solving the XOR Problem o1 Network Topology: 2 hidden nodes 1 output Desired behavior: x1 x2 o1 o2 y 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 x1 w11 w01 w21 -1 w12 x2 w13 y w23 w22 w03 -1 w02 o 2 -1 Weights: w11= w12=1 w21=w22 = 1 w01=3/2; w02=1/2; w03=1/2 w13=-1; w23=1 Backpropagation • Greedy, Hill-climbing procedure – Weights are parameters to change – Original hill-climb changes one parameter/step • Slow – If smooth function, change all parameters/step • Gradient descent – Backpropagation: Computes current output, works backward to correct error Producing a Smooth Function • Key problem: – Pure step threshold is discontinuous • Not differentiable • Solution: – Sigmoid (squashed ‘s’ function): Logistic fn n 1 z wi xi s ( z ) z 1 e i Neural Net Training • Goal: – Determine how to change weights to get correct output • Large change in weight to produce large reduction in error • Approach: • • • • Compute actual output: o Compare to desired output: d Determine effect of each weight w on error = d-o Adjust weights Neural Net Example y3 xi : ith sample input vector w : weight vector yi*: desired output for ith sample E z3 w03 1 2 * ( y F ( x i i , w)) 2 i -1 z1 Sum of squares error over training samples w13 y1 w23 y2 z2 w21 w01 -1 w1 1 z1 z2 x1 w12 w22 x2 w02 -1 y3 F ( x, w) s(w13s(w11x1 w21x2 w01 ) w23s(w12 x1 w22 x2 w02 ) w03 ) z3 Full expression of output in terms of input and weights Gradient Descent • Error: Sum of squares error of inputs with current weights • Compute rate of change of error wrt each weight – Which weights have greatest effect on error? – Effectively, partial derivatives of error wrt weights • In turn, depend on other weights => chain rule Gradient of Error 1 E ( yi* F ( xi , w)) 2 2 i z1 z2 y3 F ( x, w) s(w13s(w11x1 w21x2 w01 ) w23s(w12 x1 w22 x2 w02 ) w03 ) y3 E * ( yi y3 ) w j w j y3 z3 z3 w03 Note: Derivative of sigmoid: ds(z1) = s(z1)(1-s(z1) z1 y3 s( z3 ) z3 s( z3 ) s ( z3 ) s( z1 ) y1 w13 z3 w13 z3 z3 -1 z1 w13 y1 w23 y2 z2 w21 w01 -1 w1 1 x1 w12 w22 x2 y3 s ( z3 ) z3 s ( z3 ) s ( z1 ) z1 s( z3 ) s ( z1 ) w13 w13 x1 w11 z3 w11 z3 z1 w11 z3 z1 MIT AI lecture notes, Lozano-Perez 2000 w02 -1 From Effect to Update • Gradient computation: – How each weight contributes to performance • To train: – Need to determine how to CHANGE weight based on contribution to performance – Need to determine how MUCH change to make per iteration • Rate parameter ‘r’ – Large enough to learn quickly – Small enough reach but not overshoot target values Backpropagation Procedure i wi j w j k j k oj oi • Pick rate parameter ‘r’ o (1 o ) • Until performance is good enough, j j ok (1 ok ) – Do forward computation to calculate output – Compute Beta in output node with z d z oz – Compute Beta in all other nodes with j w j k ok (1 ok ) k k – Compute change for all weights with wi j ro j (1 o j ) j Backpropagation Observations • Procedure is (relatively) efficient – All computations are local • Use inputs and outputs of current node • What is “good enough”? – Rarely reach target (0 or 1) outputs • Typically, train until within 0.1 of target Neural Net Summary • Training: – Backpropagation procedure • Gradient descent strategy (usual problems) • Prediction: – Compute outputs based on input vector & weights • Pros: Very general, Fast prediction • Cons: Training can be VERY slow (1000’s of epochs), Overfitting Training Strategies • Online training: – Update weights after each sample • Offline (batch training): – Compute error over all samples • Then update weights • Online training “noisy” – Sensitive to individual instances – However, may escape local minima Training Strategy • To avoid overfitting: – Split data into: training, validation, & test • Also, avoid excess weights (less than # samples) • Initialize with small random weights – Small changes have noticeable effect • Use offline training – Until validation set minimum • Evaluate on test set – No more weight changes Classification • Neural networks best for classification task – Single output -> Binary classifier – Multiple outputs -> Multiway classification • Applied successfully to learning pronunciation – Sigmoid pushes to binary classification • Not good for regression Neural Net Conclusions • Simulation based on neurons in brain • Perceptrons (single neuron) – Guaranteed to find linear discriminant • IF one exists -> problem XOR • Neural nets (Multi-layer perceptrons) – Very general – Backpropagation training procedure • Gradient descent - local min, overfitting issues