* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download عرض تقديمي من PowerPoint
Survey
Document related concepts
Perceptual control theory wikipedia , lookup
Neural modeling fields wikipedia , lookup
Gene expression programming wikipedia , lookup
Hierarchical temporal memory wikipedia , lookup
Backpropagation wikipedia , lookup
Pattern recognition wikipedia , lookup
Transcript
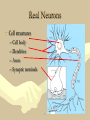
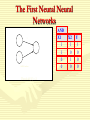
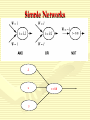
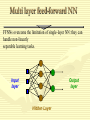
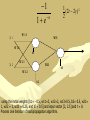
Artificial Intelligence Neural Networks History • Roots of work on NN are in: • Neurobiological studies (more than one century ago): • • How do nerves behave when stimulated by different magnitudes of electric current? Is there a minimal threshold needed for nerves to be activated? Given that no single nerve cel is long enough, how do different nerve cells communicate among each other? Psychological studies: • How do animals learn, forget, recognize and perform other types of tasks? • Psycho-physical experiments helped to understand how individual neurons and groups of neurons work. • McCulloch and Pitts introduced the first mathematical model of single neuron, widely applied in subsequent work. History • • Widrow and Hoff (1960): Adaline Minsky and Papert (1969): limitations of single-layer perceptrons (and they erroneously claimed that the limitations hold for multi-layer perceptrons) Stagnation in the 70's: • Individual researchers continue laying foundations • von der Marlsburg (1973): competitive learning and self-organization Big neural-nets boom in the 80's • Grossberg: adaptive resonance theory (ART) • Hopfield: Hopfield network • Kohonen: self-organising map (SOM) Applications • Classification: – – – – – Image recognition Speech recognition Diagnostic Fraud detection … • Regression: – Forecasting (prediction on base of past history) – … • Pattern association: – Retrieve an image from corrupted one – … • Clustering: – clients profiles – disease subtypes – … Real Neurons • Cell structures – – – – Cell body Dendrites Axon Synaptic terminals 5 Non Symbolic Representations • Decision trees can be easily read – A disjunction of conjunctions (logic) – We call this a symbolic representation • Non-symbolic representations – More numerical in nature, more difficult to read • Artificial Neural Networks (ANNs) – A Non-symbolic representation scheme – They embed a giant mathematical function • To take inputs and compute an output which is interpreted as a categorisation – Often shortened to “Neural Networks” • Don’t confuse them with real neural networks (in heads) Complicated Example: Categorising Vehicles • Input to function: pixel data from vehicle images – Output: numbers: 1 for a car; 2 for a bus; 3 for a tank INPUT OUTPUT = 3 INPUT OUTPUT = 2 INPUT OUTPUT = 1 INPUT OUTPUT=1 Real Neural Learning • Synapses change size and strength with experience. • Hebbian learning: When two connected neurons are firing at the same time, the strength of the synapse between them increases. • “Neurons that fire together, wire together.” 8 Neural Network Input Layer Hidden 1 Hidden 2 Output Layer Simple Neuron X1 W1 Inputs X2 W2 Wn Xn f Output Neuron Model • A neuron has more than one input x1, x2,..,xm • Each input is associated with a weight w1, w2,..,wm • The neuron has a bias b • The net input of the neuron is n = w1 x1 + w2 x2+….+ wm xm + b n wi xi b Neuron output • The neuron output is y = f (n) • f is called transfer function Transfer Function • We have 3 common transfer functions – Hard limit transfer function – Linear transfer function – Sigmoid transfer function Exercises • The input to a single-input neuron is 2.0, its weight is 2.3 and the bias is –3. • What is the output of the neuron if it has transfer function as: – Hard limit – Linear – sigmoid Architecture of ANN • Feed-Forward networks Allow the signals to travel one way from input to output • Feed-Back Networks The signals travel as loops in the network, the output is connected to the input of the network Learning Rule • The learning rule modifies the weights of the connections. • The learning process is divided into Supervised and Unsupervised learning Perceptron • It is a network of one neuron and hard limit transfer function X1 W1 Inputs X2 W2 Wn Xn f Output Perceptron • The perceptron is given first a randomly weights vectors • Perceptron is given chosen data pairs (input and desired output) • Preceptron learning rule changes the weights according to the error in output Perceptron • The weight-adapting procedure is an iterative method and should reduce the error to zero • The output of perceptron is Y = f(n) = f ( w1x1+w2x2+…+wnxn) =f (wixi) = f ( WTX) Perceptron Learning Rule W new = W old + (t-a) X Where W new is the new weight W old is the old value of weight X is the input value t is the desired value of output a is the actual value of output Example • Consider a perceptron that has two real-valued inputs and an output unit. All the initial weights and the bias equal 0.1. Assume the teacher has said that the output should be 0 for the input: x1 = 5 and x2 = - 3. Find the optimum weights for this problem. Example • Covert the classification problem into perceptron neural network model (start w1=1, b=3 and w2=2 or any other values). • X1 = [0 2], t1=1 & x2 = [1 0], t2=1 & x3 = [0 –2] , t3=0 & x4=[2 0], t4=0 Example Perceptron • Example calculation: x1=-1, x2=1, x3=1, x4=-1 – S = 0.25*(-1) + 0.25*(1) + 0.25*(1) + 0.25*(-1) = 0 • 0 > -0.1, so the output from the ANN is +1 – So the image is categorised as “bright” The First Neural Neural Networks X1 1 Y X2 1 AND Function Threshold(Y) = 2 AND X1 1 1 0 0 X2 1 0 1 0 Y 1 0 0 0 Simple Networks -1 W = 1.5 x t = 0.0 W=1 y Exercises • Design a neural network to recognize the problem of • X1=[2 2] , t1=0 • X=[1 -2], t2=1 • X3=[-2 2], t3=0 • X4=[-1 1], t4=1 Start with initial weights w=[0 0] and bias =0 Problems • Four one-dimensional data belonging to two classes are X = [1 -0.5 3 -2] T = [1 -1 1 -1] W = [-2.5 1.75] Example -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 +1 -1 -1 -1 -1 +1 -1 -1 +1 -1 +1 -1 -1 +1 -1 -1 +1 -1 +1 -1 -1 +1 -1 -1 +1 +1 +1 +1 +1 +1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 Example -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 +1 -1 -1 -1 -1 +1 -1 -1 -1 -1 +1 -1 -1 +1 -1 +1 -1 -1 +1 -1 -1 +1 -1 +1 -1 -1 +1 -1 -1 +1 +1 +1 +1 +1 +1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 AND Network • This example means we construct a network for AND operation. The network draw a line to separate the classes which is called Classification Perceptron Geometric View The equation below describes a (hyper-)plane in the input space consisting of real valued m-dimensional vectors. The plane splits the input space into two regions, each of them describing one class. decision region for C1 x2 w x + w x + w >= 0 m 1 1 2 2 0 w x i 1 i i w0 0 decision boundary C1 C2 x1 w1x1 + w2x2 + w0 = 0 Perceptron: Limitations • The perceptron can only model linearly separable classes, like (those described by) the following Boolean functions: • AND • OR • COMPLEMENT • It cannot model the XOR. • You can experiment with these functions in the Matlab practical lessons. Multi-layers Network • Let the network of 3 layers – Input layer – Hidden layers – Output layer • Each layer has different number of neurons Multi layer feed-forward NN FFNNs overcome the limitation of single-layer NN: they can handle non-linearly separable learning tasks. Input layer Output layer Hidden Layer Types of decision regions 1 w0 w1 x1 w2 x2 0 Network with a single node w0 x1 w1 w0 w1 x1 w2 x2 0 L1 L2 w2 1 1 1 Convex region L3 x2 x1 L4 x2 1 -3.5 1 1 One-hidden layer network that realizes the convex region Learning rule • The perceptron learning rule can not be applied to multi-layer network • We use BackPropagation Algorithm in learning process Backprop • Back-propagation training algorithm illustrated: Network activation Error computation Forward Step Error propagation Backward Step • Backprop adjusts the weights of the NN in order to minimize the network total mean squared error. Bp Algorithm • The weight change rule is ijnew ijold .error. f ' (inputi ) • Where is the learning factor <1 • Error is the error between actual and trained value • f’ is is the derivative of sigmoid function = f(1-f) Delta Rule • Each observation contributes a variable amount to the output • The scale of the contribution depends on the input • Output errors can be blamed on the weights • A least mean square (LSM) error function can be defined (ideally it should be zero) E = ½ (t – y)2 Calculation of Network Error • Could calculate Network error as – Proportion of mis-categorised examples • But there are multiple output units, with numerical output – So we use a more sophisticated measure: • Not as complicated as it looks – Square the difference between target and observed • Squaring ensures we get a positive number • Add up all the squared differences – For every output unit and every example in training set Example • For the network with one neuron in input layer and one neuron in hidden layer the following values are given X=1, w1 =1, b1=-2, w2=1, b2 =1, =1 and t=1 Where X is the input value W1 is the weight connect input to hidden W2 is the weight connect hidden to output b1 and b2 are bias t is the training value Momentum in Backpropagation • For each weight – Remember what was added in the previous epoch • In the current epoch – Add on a small amount of the previous Δ • The amount is determined by – The momentum parameter, denoted α – α is taken to be between 0 and 1 How Momentum Works • If direction of the weight doesn’t change – Then the movement of search gets bigger – The amount of additional extra is compounded in each epoch – May mean that narrow local minima are avoided – May also mean that the convergence rate speeds up • Caution: – May not have enough momentum to get out of local minima – Also, too much momentum might carry search • Back out of the global minimum, into a local minimum Building Neural Networks • Define the problem in terms of neurons – think in terms of layers • Represent information as neurons – operationalize neurons – select their data type – locate data for testing and training • Define the network • Train the network • Test the network Application: FACE RECOGNITION • The problem: – Face recognition of persons of a known group in an indoor environment. • The approach: – Learn face classes over a wide range of poses using neural network. Navigation of a car • Done by Pomerlau. The network takes inputs from a 34X36 video image and a 7X36 range finder. Output units represent “drive straight”, “turn left” or “turn right”. After training about 40 times on 1200 road images, the car drove around CMU campus at 5 km/h (using a small workstation on the car). This was almost twice the speed of any other non-NN algorithm at the time. 5/24/2017 46 Automated driving at 70 mph on a public highway Camera image 30 outputs for steering 4 hidden units 30x32 weights into one out of four hidden unit 30x32 pixels as inputs 47 Exercises • Perform one iteration of backprpgation to network of two layers. First layer has one neuron with weight 1 and bias –2. The transfer function in first layer is f=n2 • The second layer has only one neuron with weight 1 and bias 1. The f in second layer is 1/n. • The input to the network is x=1 and t=1 1 n 1 e W 11 X1 1 (2t 2 y ) 2 2 W13 W 12 b1 X2 W21 W23 W22 b3 b2 using the initial weights [b1= - 0.5, w11=2, w12=2, w13=0.5, b2= 0.5, w21= 1, w22 = 2, w23 = 0.25, and b3= 0.5] and input vector [2, 2.5] and t = 8. Process one iteration of backpropagation algorithm. Consider a transfer function as f(n) = n2. Perform one iteration of BackPropagation with a= 0.9 for neural network of two neurons in input layer and one neuron in output layer. The input values are X=[1 -1] and t = 8, the weight values between input and hidden layer are w11 = 1, w12 = - 2, w21 = 0.2, and w22 = 0.1. The weight between input and output layers are w1 = 2 and w2= -2. The bias in input layers are b1 = -1, and b2= 3. W11 W1 X1 W12 W21 W2 X2 W22 QUIZ Quiz • Briefly describe the Turing Test • Do you agree that if a computer passes the Turing Test then it does not prove that the computer is intelligent? State your reasons. 2 8 7 3 1 4 5 6 1. Using breadth first search, show the search tree that would be built down to level 2 (assume level zero is the root of the tree). 2. Using depth first search, show the state of the search tree down the level 3 (stop once you have expanded one node that goes to level 3) 3. Implement the search algorithm using data structure methods as you can