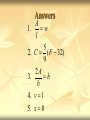Download Solving Absolute Value Equations

Warm Up
Solve.
1. A=lw for w
4. -3v + 6 = 4v – 1
9
2. F  C  32 for C
5
5. 3(2x – 4) = 4x + 4
1
3. A  bh for h
2
Answers
1.
2.
3.
4.
A
w
l
5
C  ( F  32)
9
2A
h
b
v 1
5. x  8
Lesson 3.4 Solving Absolute
Value Equations
1.1.3
Exploration

Determine the solution for each equation.

x 4
4, -4

n 9
9, -9

c  6
No Solution
What did you notice?

Summarize what you noticed from the
previous solutions.
When a variable is inside an absolute value, there
are two solutions.
 When an absolute value is set equal to a negative
number, there is no solution. (this is important to
remember)
 Can you think of a situation where there would be
one solution? When the absolute value is equal to zero.


Steps for solving
absolute value
equations.
1. Distribute
2. Combine Like Terms
3. Move Variable to One Side
4. Undo + or –
5. Undo × or ÷
**Need to isolate the absolute
value expression**
1)
Undo addition or
subtraction outside of
absolute value.
2)
Undo multiplication or
division outside of absolute
value.
3)
Set expression inside
absolute value equal to the
given value and its opposite.
4)
Solve for variable using
steps for solving equations.
Examples

Solving basic
absolute value
equations
1.
x  5  12
x  5  12 and x  5  12
x  5  12 and x  5  12
5 5
x  17
5
5
x  7
Examples continued
2. 2 x  6  4
1, 5
1
3.
x4 8
2
-24, 8
More Examples

Solving
absolute value
equations
when there are
terms outside
the symbols
x  1  4  12
1.
x  1  4  12
4 4
x  1  16
x 1  16 and x 1  16
x 1  16 and x 1  16
1
1
1
1
x  15 and x  17
Even More Examples
5.
3x  4  6  10
0, 8/3
6. 3 2 x  4  6  18
-2, 6
Summary/Reflection

What is the difference between solving a
regular equation and solving an equation
where the variable is in an absolute value?

How can you remember that absolute value
equations have two solutions?
Homework
3.4 worksheet