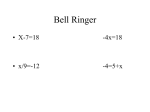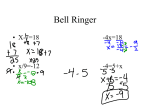Download Rational Exponents 1 Answers

Accelerated CCGPS…Math II
Name
Rational Exponents
Period_____Date_______________
What is 52?
25
What is 23?
8
What is 51?
5
What is x1?
x
Answers
.
What is (52)3? 15625 What is (2-3)2 ? 1/64
_What is x0?
What is 4(¼)?
1
1
.
.
One way to solve equations is to think of the equation as a balance and we must work with both
sides to “undo” what was done to the variable. For example, if 4x + 7 = 31, we must “undo”
adding 7, so subtract 7 from each side, yielding 4x = 24. Then we must “undo” multiplying by 4,
so we divide both sides by 4, yielding x = 6.
Solve the following equations by “undoing”:
2
5
1
6x + 8 = 38
5(x – 8) = 50
x 5  x 
3
6
2
5x  40  50
11
1
6x  30

 x
5x  90
2
6
x 5
x  18
x   33
A little more vocabulary: Consider the expression
36 . What is the radicand?
36
.
What is the index? 2
What is the value of 36 ?
6
Explain your thought process to
get this value. What number, times itself, would produce 36.
For the expression
is the value of
3
3
125 , what is the radicand?
125 ?
5
125
What is the index?
3
What
.
Explain your thought process to get this value?
What number, times itself, then times itself again, would produce 125.
4
3 27 =
4 81 = _ 3
=
2/3
3
9
Furthermore, some irrational numbers in radical form can be simplified. For example:
Find these values:
24  4 6  4
3 54
 3 27 2  3 27
81 =
9
6 2 6
32
 33 2
and
5

8
5 2

8 2
10
10
10


16
4
16
.
and
(Note that we look for perfect squares/cubes.)
x 2  25
If we know that x2 = 25, how do we “undo” squaring a number?
Show the steps to solve this equation.
If we know that x3 = 8, how do we “undo” cubing a number?
Show the steps to solve this equation.
3
x 5
x3 
3
x 2
8
Another way to think of solving these equations is to force the exponent of x to be 1. What
would that entail?
How would that look?
1
25  25 2 =
That would mean that
 
52
1
2
5
and
3
1
8  83 =
 
23
1
3
2
So what would these values be?
1
49 2
=
7 
2
1
2
1
64 3
7
Furthermore, since
2
83
4 
3
=
1
3
4
1
100000 5
=
10 
5
1
5
2
1
2
1
 
4
 10
2

 1
  8 3  , what would 8 3 equal?  2 3
 

 

 
1
3
1
 1 2  2
1
=    
2
 2  


2

2
  2   4


So find these values!

3
36 2
2
1
4
 8 3
1 2

3=
=
216
=
3
=
4/9
1/625 .

125




 
9
 27 
 Be careful to consider what the negative sign means in an exponential position as
opposed to what it means as a factor of a number!
For Homework, rewrite these numbers in a different form. Change radicals to positive
fractional exponents and vice versa.
1
2
1.
42
 42
2.
3
15
 15 3
3.
5
34
 35
4.
5. 14
 
7. 24

1
2
 35
1

5
4
4
 3 16  2 3 2
6. 16 3
4
14

1
1
53
1
2
24

72
2.
3
4
3.
3
5
6 2

1
1
400

1
2

1
20

4
7

4
49
1
3
 16  2
7. 

 49 
2
1
15
5
16 2
8.
49
 12
9. 64 3

4. 144 2
6.
4
1
5. 1000 3  1000 3
 10  10 
20
12
 3 4 5  4 3 16
8. 4 3
Simplify each of the following expressions completely:
1.
6
 256
2
10. 1000 3
 100