Download Localized surface plasmon resonances

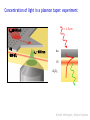
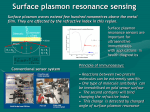
Nanophotonics
Class 2
Surface plasmon polaritons
Surface plasmon polariton: EM wave at metal-dielectric
interface
z
x

 i k x  k z t 
Ed x, z, t   Ed ,0e x z

 i k xk z t 
Em ( x, z, t )  Em,0e x z
For propagating
bound waves:
- kx is real
- kz is imaginary
EM wave is coupled to the plasma oscillations of the surface charges
Derivation of surface plasmon dispersion relation: k()
2 
2
 Ed ,m
2
k
Wave equation:  E d , m   0  d , m 0 d , m
2

t
Substituting SP wave + boundary conditions leads to the
Dispersion relation:
x-direction:
   m d
k x  k ' x ik "x  
c  m  d
1/ 2



  



k



Note: in regular dielectric: 
c


k
Dispersion relation:
x-direction:
z-direction:
   m d
k x  k ' x ik "x  
c  m  d
k z ,m
 
2

1/ 2



1/ 2
  


 k ' z ,m ik"z ,m 
c   m   d 
 m2
Bound SP mode: kz imaginary: m + d < 0, kx real: m < 0
so: m < -d




k 
c


Dielectric constant of metals
Drude model: conduction electrons with damping: equation of motion
d 2x
dx
m 2  m
 eE0 e it
dt
dt
no restoring force
2
 p2
P
Nex
Ne
  1
 1
 1
 1 2
2
0E
0E
m 0   i
  i



with collision frequency  and plasma frequency
If  << p, then:
 p2
 p2
 '  1 2 , " 3 


Ne 2
p 
m 0

Measured data and model for Ag:
Drude model:
50
 p2
 p2
 '  1 2 , " 3 


"
0

-50
-100
Measured data:
'
"
Drude model:
'
"
Modified Drude model:
'
Modified Drude model:
'
 p2
 p2
 '    2 , " 3 


-150
200
400
600
800
1000
1200
Wavelength (nm)
1400
1600
1800
Contribution of
bound electrons
Ag:
   5.45
Bound SP modes: m < -d
50
"
0

-50
-100
-d
Measured data:
'
"
'
Drude model:
'
"bound SP mode:  < -
m
d
Modified Drude model:
'
-150
200
400
600
800
1000
1200
Wavelength (nm)
1400
1600
1800
   m d
Surface plasmon dispersion relation: k x  
c  m  d

ck x
Radiative modes
d
'm > 0)
1/ 2



real kx
real kz
p
Quasi-bound modes
d < 'm <
0)
p
imaginary kx
real kz
1 d
Dielectric: d
z
x
Bound modes
('m < d)
Metal: m = m' + m"
Re kx
real kx
imaginary kz
   m d
Surface plasmons dispersion: k x  
c  m  d
ck x

d
1/ 2



large k
small wavelength
3.4 eV
(360 nm)
Ag/SiO2
Ar laser:
vac = 488 nm
diel = 387 nm
SP = 100 nm
X-ray wavelengths
at optical frequencies
k
Re kx
2

Surface plasmon dispersion for thin films
Drude model
Two modes appear
ε1(ω)=1-(ωp/ω) 2
Thinner film:
Shorter SP
wavelength
Propagation
lengths: cm !!!
(infrared)
Example:
HeNe = 633 nm
SP = 60 nm
LL-(symm)
L+(asymm)
Cylindrical metal waveguides
E
Fundamental
SPP mode
on cylinder:
•
E
r
z
k
Can this adiabatic coupling
scheme be realized in
practice?
taper theory first demonstrated by
Stockman, PRL 93, 137404 (2004)
Delivering light to the nanoscale
E
+++
+ +
++
2.3
neff = kSPP/k0
2.2
nanoscale
confinement
|E|
Field symmetry at tip
similar to SPP mode in
conical waveguide
2.1
1 µm
2.0
E
z
x
1.9
1 µm
1.8
k
1.7
0.0
0.2
0.4
0.6
0.8
1.0
Waveguide width (µm)
Optics Express 16, 45 (2008)
Ewold Verhagen, Kobus Kuipers
Concentration of light in a plasmon taper: experiment
λ = 1.5 μm
Au
Er
Al2O3
Ewold Verhagen, Kobus Kuipers
Concentration of light in a plasmon taper: experiment
10 µm
(1490 nm)
PL Intensity (counts/s)
1 µm
Er3+ energy levels
60 nm apex diam.
transmission
exc = 1490 nm
Nano Lett. 7, 334 (2007)
Ewold Verhagen, Kobus Kuipers
Concentration of light in a plasmon taper: experiment
•
Detecting upconversion luminescence from the air side of the film (excitation
of SPPs at substrate side)
550 nm
660 nm
E
z
x
k
Plasmonic hot-spot
Theory: Stockman, PRL 93, 137404 (2004)
Optics Express 16, 45 (2008)
Ewold Verhagen, Kobus Kuipers
FDTD Simulation: nanofocussing to < 100 nm
|E|2
z = -35 nm
sym
asym
Et, H
1 µm
E
+ ++
++ ++
n1 = 1
n2 = 1.74
•
•
•
1 µm
Nanofocusing predicted: 100 x |E|2
at 10 nm from tip
3D subwavelength confinement:
1.5 µm light focused to 92 nm (/16)
limited by taper apex (r=30 nm)
start
tip
Optics Express 16, 45 (2008)
Ewold Verhagen, Kobus Kuipers
Coaxial MIM plasmon waveguides
FIB milling of coaxial waveguides
<w>=100 nm, L=485 nm
100 nm
<w>=50 nm, L=485 nm
100 nm
• Silica substrates with 250-500 nm thick Ag
• Ring width: 50-100 nm
• Two-step milling process
• ~7° taper angle
Nano Lett. 9, in press (2009)
René de Waele, Stanley Burgos
Narrow channels show negative index
• Excitation above
resonance, >sp
• 25 nm-wide channel
in Ag filled with GaP
• Simulation shows
negative phase
velocity with respect
to power flow
• Negative refractive
index of -2
René de Waele, Stanley Burgos
Positive and negative index modes
René de Waele, Stanley Burgos
Plasmonic toolbox: , (), d - Engineer ()
Plasmonic integrated circuits
Plasmonic concentrator
Plasmonic multiplexer
Plasmonic lens
thin section
Y Axis Title
1.0
0.5
0.0
-0.5
-1.0
0
200
400
600
Distance (nm)
800
1000
And much more …..
Conclusions: surface plasmon polariton
Surface plasmon: bound EM wave at metal-dielectric interface
Dispersion: (k) diverges near the plasma resonance: large k, small 
Control dispersion: control (k), losses, concentration
Manipulate light at length scales
below the diffraction limit