* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
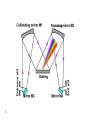
Fourier optics wikipedia , lookup
Diffraction topography wikipedia , lookup
Lens (optics) wikipedia , lookup
Anti-reflective coating wikipedia , lookup
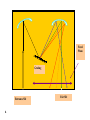
Optical rogue waves wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Retroreflector wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Optical aberration wikipedia , lookup
Atomic absorption spectroscopy wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Fiber Bragg grating wikipedia , lookup
Dispersion staining wikipedia , lookup
Diffraction wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Components of Optical Instruments, Cont… Lecture 7 1 Monochromators A monochromator is the part of instrument responsible for producing monochromatic radiation. It is an essential component of any spectroscopic instrument and is composed of a prism or grating, as the l selector, in addition to focusing elements; like mirrors or lenses. All these components are contained in a box that has an entrance and an exit slit. Two common types of monochromators can be described: 2 Czerney-Turner Grating Monochromator This is composed of a grating, two concave mirrors and two slits. The following setup can be associated with this monochromator system: 3 Focal Plane Grating Entrance Slit 4 Exit Slit 5 6 Bunsen Prism Monochromators This type of monochromators uses a prism as the dispersion element in addition to two focusing lenses and two slits. The setup can be depicted as in the figure below: 7 Collimating Lens Focusing Lens Focal Plane Entrance Slit Exit Slit Prism 8 9 10 Performance Characteristics of Grating Monochromators Four main properties can assess the performance of grating monochromators. These include the following: 1. Spectral Purity If the exiting beam is thoroughly studied, it will always be observed that it is contaminated with small amounts of wavelengths far from that of the instrumental setting. This is mainly due to the following reasons: 11 a. Scattered radiation due to presence of dust particulates inside the monochromator as well as on various optical surfaces. This drawback can be overcome by sealing the monochromator entrance and exit slits by suitable windows. 12 b. Stray radiation which is radiation that exits the monochromator without passing through the dispersion element. This problem as well as all other problems related to spurious radiation, including scattering, can be largely eliminated by introducing baffles at appropriate locations inside the monochromator, as well as painting the internal walls of the monochromator by a black paint. 13 c. Imperfections of monochromator components, like broken or uneven blazes, uneven lens or mirror surfaces, etc, would lead to important problems regarding the quality of obtained wavelengths. 14 2. Dispersion of Grating Monochromators Dispersion is the ability of a monochromator to separate the different wavelengths. The angular dispersion can be defined as the change in the angle of reflection with wavelength: Angular dispersion = dr/dl We have previously seen that: nl = d(sin i +sin r) differentiating this equation at constant angle of incidence gives: 15 n dl = d cos r dr which gives upon rearrangement: dr/dl = n/d cos r In fact, we are more interested in the linear dispersion (change of the distance at the focal plane with wavelength), D where: D = dy/dl Where; y is the distance along the focal plane. If the focal length of the focusing mirror is F, then: dy = Fdr substitution in the linear dispersion equation gives: D = Fdr/dl 16 A widely used parameter for expressing the dispersion of grating monochromators is the inverse of the linear dispersion. This is called reciprocal linear dispersion, D-1 = 1/D D-1 = dl/Fdr but we have dr/dl = n/d cos r Therefore, one can write: D-1 = d cos r/nF At small reflection angles (<20o) cos r approximates to unity which suggests that: D-1 = d/nF or D = nF/d 17 3. Resolving Power of a Grating Monochromator The ability of a grating monochromators to separate adjacent wavelengths, with very small difference, is referred to as the resolving power of the grating monochromator, R. R = l/Dl where: Dl is the difference between the two adjacent wavelengths (l2 – l1) and l is their average (l1 + l2)/2 18 The resolving power can also be defined as: R = nN Where n is the diffraction order and N is the number of illuminated blazes. Therefore, better resolving powers can be obtained for: a. Longer gratings. b. higher blaze density. c. Higher order of diffraction. 19 4. Light Gathering Power The ability of a grating monochromator to collect incident radiation from the entrance slit is very important as only some of this radiation will reach the detector. The speed or f/number is a measure of the ability of the monochromator to collect incident radiation. f = F/d where; F is the focal length of the collimating mirror or lens and d is its diameter. 20 The light gathering power of a grating monochromator increases as the inverse square of the f/number. LGP(1) = 1/(f/n)2 The f/number for most monochromators ranges from 1 to 10. For Example: If monochromator 1 has an f/1 and monochromator 2 has an f/2, the light gatehring power of the two monochromators can be compared as follows: LGP(1) / LGP (2) = 22/12 = 4 21 This means that the light gathering power of the monochromator 1 is 4 times monochromator 2. If monochromator 1 has an f/2 and monochromator 2 has an f/8, the light gatehring power of the two monochromators can be compared as follows: LGP(1) / LGP (2) = 82/22 = 16 This means that the light gathering power of the monochromator 1 is 16 times monochromator 2. 22 Monochromator Slits Slits of a monochromator are very important for its performance. It may be primitive to say that multiple wavelengths hitting the focal plane can emerge from the exit slit if the exit slit is too wide. On the other hand, a beam of very low power can emerge from the exit slit when the slit is too narrow. The first case leads to bad wavelength selection (bad resolution) as a mixture of wavelengths is obtained, while the other case may make it impossible for the detector to sense the low power beam (bad detectability). Therefore, the width of the slits should be carefully adjusted, where some instruments allow such adjustments. 23 However, many instruments have fixed slit monochromators optimized for general purpose applications. A slit is machined from two pieces of metal to give sharp edges that are exactly aligned (same plane) and parallel. The entrance slit of a monochromator can be looked at as a radiation source with an image that will exactly fill the exit slit at a particular grating setting. Images from other wavelengths will align at the focal plane of the monochromator. An image of interest can be brought to focus by appropriate rotation of the grating. 24