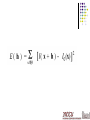* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Week 10 (4/20/2006)
Survey
Document related concepts
Transcript
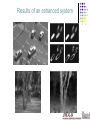
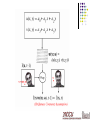
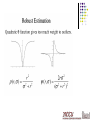
Optical Flow Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Optical Flow: Where do pixels move to? Motion is a basic cue Motion can be the only cue for segmentation Applications tracking structure from motion motion segmentation stabilization compression mosaicing … Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Definition of optical flow OPTICAL FLOW = apparent motion of brightness patterns Ideally, the optical flow is the projection of the three-dimensional velocity vectors on the image Caution required ! Two examples : 1. Uniform, rotating sphere O.F. = 0 2. No motion, but changing lighting O.F. 0 Mathematical formulation I (x,y,t) = brightness at (x,y) at time t Brightness constancy assumption: dx dy I ( x t , y t , t t ) I ( x, y, t ) dt dt Optical flow constraint equation : dI I dx I dy I 0 dt x dt y dt t Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion The aperture problem dx u dt I I x y dy v dt I I y y I It t I xu I y v I t 0 1 equation in 2 unknowns The Aperture Problem 0 What is Optical Flow, anyway? Estimate of observed projected motion field Not always well defined! Compare: Motion Field (or Scene Flow) projection of 3-D motion field Normal Flow observed tangent motion Optical Flow apparent motion of the brightness pattern (hopefully equal to motion field) Consider Barber pole illusion Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Horn & Schunck algorithm Additional smoothness constraint : es (( ux2 u 2y ) (vx2 v 2y )) dxdy, besides OF constraint equation term ec ( I x u I y v I t )2 dxdy, minimize es+ec Horn & Schunck The Euler-Lagrange equations : Fu Fux Fu y 0 x y Fv Fvx Fv y 0 x y In our case , F (u u ) (v v ) ( I xu I y v I t ) , 2 x 2 y 2 x 2 y so the Euler-Lagrange equations are u ( I x u I y v I t ) I x , v ( I xu I y v I t ) I y , 2 2 2 2 x y is the Laplacian operator 2 Horn & Schunck Remarks : 1. Coupled PDEs solved using iterative methods and finite differences u u ( I x u I y v I t ) I x , t v v ( I x u I y v I t ) I y , t 2. More than two frames allow a better estimation of It 3. Information spreads from corner-type patterns Horn & Schunck, remarks 1. Errors at boundaries 2. Example of regularization (selection principle for the solution of ill-posed problems) Results of an enhanced system Structure from motion with OF Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion dE (u, v) 2 I x I xu I y v I t 0 du dE (u, v) 2 I y I xu I y v I t 0 dv Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Bayesian flow Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Optical Flow Brightness Constancy The Aperture problem Regularization Lucas-Kanade Coarse-to-fine Parametric motion models Direct depth SSD tracking Robust flow Textured motion Optical Snow http://www.cim.mcgill.ca/~langer/research-opticalsnow.html Optical snow is the type of motion an observer sees when watching a snow fall. Flakes that are closer to the observer appear to move faster than flakes which are farther away. Textured Motion http://civs.stat.ucla.edu/Yizhou_Research/Tex turedmotion.htm Natural scenes contain rich stochastic motion patterns which are characterized by the movement of a large amount of particle and wave elements, such as falling snow, water waves, dancing grass, etc. We call these motion patterns "textured motion".