* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Phys132 Lecture 5 - University of Connecticut
Ray tracing (graphics) wikipedia , lookup
Optical flat wikipedia , lookup
Diffraction grating wikipedia , lookup
Birefringence wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
Retroreflector wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Nonlinear optics wikipedia , lookup
Diffraction wikipedia , lookup
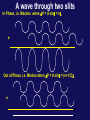
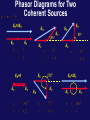
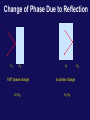
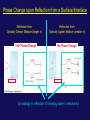
Physics 1402: Lecture 33 Today’s Agenda • Announcements: – Midterm 2: graded after Thanks Giving – Homework 09: Friday December 4 • Optics – interference A wave through two slits In Phase, i.e. Maxima when DP = d sinq = nl Out of Phase, i.e. Minima when DP = d sinq = (n+1/2)l d q DP=d sinq Screen A wave through two slits In Phase, i.e. Maxima when DP = d sinq = nl + Out of Phase, i.e. Minima when DP = d sinq = (n+1/2)l + The Intensity What is the intensity at P? The only term with a t dependence is sin2( ).That term averages to ½ . If we had only had one slit, the intensity would have been, So we can rewrite the total intensity as, with The Intensity We can rewrite intensity at point P in terms of distance y Using this relation, we can rewrite expression for the intensity at point P as function of y Constructive interference occurs at where m=+/-1, +/-2 … Phasor Addition of Waves Consider a sinusoidal wave whose electric field component is E2(t) E1(t) E0 wt+f E0 wt Consider second sinusoidal wave E2(t) The projection of sum of two phasors EP is equal to EP(t) E1(t) f/2 f ER wt E0 E0 Phasor Diagrams for Two Coherent Sources ER=2E0 ER 450 E0 E0 E0 ER=0 E0 E0 E0 ER E0 E0 ER 900 E0 2700 E0 ER=2E0 E0 E0 SUMMARY 2 slits interference pattern (Young’s experiment) How would pattern be changed if we add one or more slits ? (assuming the same slit separation ) 3 slits, 4 slits, 5 slits, etc. Phasor: 1 vector represents 1 traveling wave single traveling wave 2 wave interference N-slits Interference Patterns F=0 F=90 F=180 F=270 F=360 N=2 N=3 N=4 Change of Phase Due to Reflection Lloyd’s mirror P2 S P1 L I Mirror The reflected ray (red) can be considered as an original from the image source at point I. Thus we can think of an arrangement S and I as a double-slit source separated by the distance between points S and I. An interference pattern for this experimental setting is really observed ….. but dark and bright fringes are reversed in order This mean that the sources S and I are different in phase by 1800 An electromagnetic wave undergoes a phase change by 1800 upon reflecting from the medium that has a higher index of refraction than that one in which the wave is traveling. Change of Phase Due to Reflection n1 n2 1800 phase change n1<n2 n1 no phase change n1>n2 n2 Interference in Thin Films 1800 phase change 1 Air Film Air no phase change 2 A wave traveling from air toward film undergoes 1800 phase change upon reflection. The wavelength of light ln in the medium with refraction index n is t The ray 1 is 1800 out of phase with ray 2 which is equivalent to a path difference ln/2. The ray 2 also travels extra distance 2t. Constructive interference Destructive interference Chapter 33 – Act 1 Estimate minimum thickness of a soap-bubble film (n=1.33) that results in constructive interference in the reflected light if the film is Illuminated by light with l=600nm. A) 113nm B) 250nm C) 339nm Problem Consider the double-slit arrangement shown in Figure below, where the slit separation is d and the slit to screen distance is L. A sheet of transparent plastic having an index of refraction n and thickness t is placed over the upper slit. As a result, the central maximum of the interference pattern moves upward a distance y’. Find y’ where will the central maximum be now ? Solution Phase difference for going though plastic sheet: Corresponding path length difference: Angle of central max is approx: Thus the distance y’ is: gives Phase Change upon Reflection from a Surface/Interface Reflection from Optically Denser Medium (larger n) 180o Phase Change Reflection from Optically Lighter Medium (smaller n) No Phase Change by analogy to reflection of traveling wave in mechanics constructive: 2t = (m +1/2) ln destructive: 2t = m ln constructive: 2t = m ln destructive: 2t = (m +1/2) ln Examples : Application Reducing Reflection in Optical Instruments