* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download New copy APSI STATS
Survey
Document related concepts
Transcript
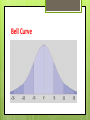
A quick introduction, discussion and conclusion of what you need to know about Statistics to be successful on the AP Psychology Exam This material was originally taken and modified from a TOPSS unit lesson plan Join TOPSS today! Fear Free Stats! Intro to STATS Statistics (Stats) can be used as a tool to help demystify research data. Examples: Election polls Market research Exercise regimes Surveys Etc. Definition of Statistics A means of organizing and analyzing data (numbers) systematically so that they have meaning. Types Descriptive StatsOrganize data so that we can communicate about that data Inferential StatsAnswers the question, “What can we infer about the population from data gathered from the sample?” Generalizability Measurement Scales Nominal Scale Ordinal Scale Interval Scale Ratio Scale Looking at data in a meaningful way Frequency distribution- an organized list that enables us to see clusters or patterns in data Example: 91 92 87 99 83 84 82 93 89 91 85 94 91 98 90 99 98 97 96 95 94 93 92 91 1 1 0 0 0 1 1 1 3 90 89 88 87 86 85 84 83 82 1 1 0 1 0 1 1 1 1 N=15 Grouped Frequency of same scores 95-99 90-94 85-89 80-84 N=15 2 7 3 3 The width of the intervals in grouped frequency tables must be equal. There should be no overlap. The Challenger Disaster Intro 30 sec 7 mins Misuse of Stats The decision to launch the Challenger was in part based on the correlational analysis of failure rates and temperature. You can look at the actual data available to the experts who decided to launch the shuttle and decide if you would have actually launched the shuttle. Temp failures 53 57 58 63 70 75 # of 2 1 1 1 2 2 The Data: Table A Temp / # of failures 53 2 57 1 63 1 66 0 67 0 68 0 69 0 70 2 72 0 73 0 75 0 76 0 79 0 81 0 The Data Table B What other factors impacted the decision of the company to allow for the launch of the Challenger? Just a moment for Discussion To the teacher: a brief research of the issue can be done to expand this topic. Application of critical thinking skills is an important marker for success on the AP Exam. Moving on to Graphs These allow us to quickly summarize the data collected. In a glance we can attain some level of meaning from the numbers. Examples: Pie Charts A circle within which all of the data points or numbers are contained in the form of percentages Bar Graphs A common method for representing nominal data where the height of the bars indicates percentage or frequency of each category Frequency Polygons A line graph that has the same vertical and horizontal labels as the histogram Each score’s frequency of occurrence is marked with a point on the graph, when all points are connected with a line The Frequency Polygon Useful in showing the asymmetry in distribution of ordinal, interval and ratio data. This asymmetry is referred to as SKEW. Positive and Negative SKEW If there is a clustering of data on the high end, then the skew is NEGATIVE because skewness is always indicative of the “tail” or low end of the graph as indicated by low frequency of occurrence. A POSITIVE skew would be indicated by high frequency of low end data points with a few data points at the high end The Tail Tells the Tale frequency polygon “tails off” to include these low frequency ends or SKEWNESS The line of the Line Graphs Indicate change that occurs during an experiment. Shows the change in relationship between IV and DV DV always on the vertical axis(Y) and IV on horizontal axis(X) ****** Graphs don’t lie But different representations will provide a different visual that can be deceptive. Dice and distribution Descriptive Statistics Measures of central tendency- these numbers attempt to describe the “typical” or “average” score in a distribution. What are the measures of central tendency? Mode The most frequently occurring score in a set of scores. When two different scores occur most frequently it is referred to as bimodal distribution. Example? Median The score that falls in the middle when the scores are ranked in ascending or descending order. This is the best indicator of central tendency when there is a skew because the median is unaffected by extreme scores. If N is odd, then the median will be a whole number, if N is even, the position will be midway between the two values in the set. Mean The mathematical average of a set of scores The mean is always pulled in the direction of extreme scores (pulled toward the skew) of the distribution. Examples? Examples SAMPLE TEMPERATURES Week One: 71 74 76 79 98 Week Two: 70 74 76 77 78 CALCULATE MEAN OF WEEK ONE MEAN OF WEEK TWO MEDIAN OF WEEK ONE MEDIAN OF WEEK TWO MODE OF WEEK ONE MODE OF WEEK TWO MEASURE OF CENTRAL TENDENCY CAN BE MISLEADING Suppose your mother wants you to attend a family reunion on Sunday. Everyone in the family protests! Your mother attempts to separately convince each family member that it will not be so bad. Mom’s story Mom tells your younger sister that the “average” age of the gathering is 10 years old. She tells you the “average” age is 18. She tells dad that the “average” age is 36. Now each family member feels better about spending the day at the family reunion. Did Mom lie? The attendees Years old 3 Name/relation 7 10 10 15 17 18 44 49 58 59 82 96 Cousin Susie Cousin Sammy Twin Shanda Twin Wanda Cousin Marty Cousin Juan Cousin Pat Aunt Harriet Uncle Stewart Aunt Rose Uncle Don Grandma Faye Great Aunt Lucille Answer me this What is the median? What is the mode? What is the mean? Did Mom “lie”? What is the median? 18 What is the mode? 10 What is the mean? 36 Did Mom “lie”? Not really. . . Measures of Variability Measures of variability indicate how much spread or variability there is in a distribution. If you collected the ages of all students in the 11th grade, there would be little variability. If you collected the shoe sizes of all students in the 11th grade, there would be greater variability. Range The range is the difference between the lowest and highest score in the data set. The range of scores can be significantly increased with a single outlying score. EXAMPLE Class One: 94, 92, 85, 81, 80, 73, 62 Range=32 Class Two: 85, 83, 82, 81, 80, 79, 77 Range= 8 Variance This is a measure of how different the scores are from each other. The difference between the scores is measured by the distance of each score from the mean of all the scores. FORMULA: Variance= Standard Deviation squared SD2 Standard Deviation This measure of variability is also based on how different scores are from each other. There are computer programs and calculators used for this data. FORMULA: The Standard Deviation is the square root of the variance Normal Distribution The normal curve is a theoretical or hypothetical frequency curve. Most frequency curves are not symmetrical (remember skew) Normal distribution is displayed on a graph with a “bell” shaped curve. Bell Curve %%%%%%%%%%% Must be memorized Correlations Correlation describes the relationship between two variables How is studying related to grades? How is playing video games related to grades? Positive Correlation Indicates a direct relationship between variables Variables move in the same direction An increase of one variable is accompanied by an increase in another variable A decrease in one variable is accompanied by a decrease in another variable Example Negative Correlation Indicates an inverse relationship between variables An increase in one variable is accompanied by a decrease in another variable, or vice versa. Correlation coefficients Correlations are measured with numbers ranging from -1.0 to +1.0. These numbers are called correlation coefficients. As the correlation coefficient moves closer to +1.0, the coefficient shows an increasing positive correlation. As the correlation coefficient moves closer to 1.0, the stronger the negative correlation. A zero could indicate no correlation exists between variables .+1.0 and -1.0 indicate a perfect correlation Which is a stronger correlation? -.85 or +.62 +.45 or -.23 -.70 or +.70 The absolute value of the number indicates the strength of the correlation. BUT. . . Correlation does not imply causation! Correlational Studies An often used research design. May not have IV and DV, may be variable one and two. Examples? Scatter plots A visual representation of correlations The x variable is on the horizontal axis and the y variable is on the vertical axis Back to the Challenger Disaster Plot the data from Table A and from Table B to establish a visual representation of the scatterplot. Inferential Statistics Help us determine if one variable has an effect on another variable. Helps us determine if the difference between variables is significant enough to infer (for credit on an AP Exam, you cannot use the term to define the term) that the difference was due to the variables, rather than chance. Statistical Significance Are the results of research strong enough to indicate a relationship (correlation)? Would you publish the results? An arbitrary criterion has been established as .05 (5%). Researchers commonly use two inferential to measure significance T-test ANOVA tests Are you free of fear? Statistics is an important aspect of research design in psychology. In college you will take an entire course in the Statistics of psychology. If you have a grasp of what was presented today, you will be successful on the AP Exam. Concept Map by Alexis Grosofsky, Ph.D., Beloit College It is a wonderful reference for you and your students. Look for it in the “references” folder Fun with STATS Dice M and distribution and M sampler