Download 02-w11-stats250-bgunderson-chapter-3-and-4

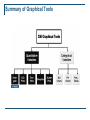
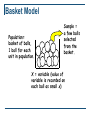
Author(s): Brenda Gunderson, Ph.D., 2011
License: Unless otherwise noted, this material is made available under the
terms of the Creative Commons Attribution–Non-commercial–Share
Alike 3.0 License: http://creativecommons.org/licenses/by-nc-sa/3.0/
We have reviewed this material in accordance with U.S. Copyright Law and have tried to maximize your
ability to use, share, and adapt it. The citation key on the following slide provides information about how you
may share and adapt this material.
Copyright holders of content included in this material should contact [email protected] with any
questions, corrections, or clarification regarding the use of content.
For more information about how to cite these materials visit http://open.umich.edu/education/about/terms-of-use.
Any medical information in this material is intended to inform and educate and is not a tool for self-diagnosis
or a replacement for medical evaluation, advice, diagnosis or treatment by a healthcare professional. Please
speak to your physician if you have questions about your medical condition.
Viewer discretion is advised: Some medical content is graphic and may not be suitable for all viewers.
Attribution Key
for more information see: http://open.umich.edu/wiki/AttributionPolicy
Use + Share + Adapt
{ Content the copyright holder, author, or law permits you to use, share and adapt. }
Public Domain – Government: Works that are produced by the U.S. Government. (17 USC § 105)
Public Domain – Expired: Works that are no longer protected due to an expired copyright term.
Public Domain – Self Dedicated: Works that a copyright holder has dedicated to the public domain.
Creative Commons – Zero Waiver
Creative Commons – Attribution License
Creative Commons – Attribution Share Alike License
Creative Commons – Attribution Noncommercial License
Creative Commons – Attribution Noncommercial Share Alike License
GNU – Free Documentation License
Make Your Own Assessment
{ Content Open.Michigan believes can be used, shared, and adapted because it is ineligible for copyright. }
Public Domain – Ineligible: Works that are ineligible for copyright protection in the U.S. (17 USC § 102(b)) *laws in
your jurisdiction may differ
{ Content Open.Michigan has used under a Fair Use determination. }
Fair Use: Use of works that is determined to be Fair consistent with the U.S. Copyright Act. (17 USC § 107) *laws in your
jurisdiction may differ
Our determination DOES NOT mean that all uses of this 3rd-party content are Fair Uses and we DO NOT guarantee that
your use of the content is Fair.
To use this content you should do your own independent analysis to determine whether or not your use will be Fair.
Empirical Rule
For bell-shaped histograms, approx…



68% of values fall within 1 standard deviation
of mean in either direction.
95% of values fall within 2 standard deviations
of mean in either direction.
99.7% of values fall within 3 standard deviations
of mean in either direction.
A very useful frame of reference!
Typical Amount of Sleep
Exercises 2.76, 2.77 pg 64:
Typical amount of sleep per night for college students
has a bell-shaped distribution with a mean of 7 hours
and a standard deviation of 1.7 hours.
About 68% of college students typically sleep between
__________ and _________ hours per night.
About 95% of college students typically sleep between
3.6 and 10.4 hours per night.
About 99.7% of college students typically sleep between
1.9 and 12.1 hours per night.
Typical Amount of Sleep
Exercises 2.76, 2.77 pg 64:
Typical amount of sleep per night for college students
has a bell-shaped distribution with a mean of 7 hours
and a standard deviation of 1.7 hours.
Draw a picture…
Typical Amount of Sleep
Exercises 2.76, 2.77 pg 64:
Typical amount of sleep has bell-shaped distribution
with mean = 7 hours and std dev = 1.7 hours.
Suppose last night you slept 11 hours.
How many standard deviations from the mean are you?
Suppose last night you slept only 5 hours.
How many standard deviations from the mean are you?
Standard Score or z-score
observed value  mean
z
standard deviation
Empirical Rule (in terms of z-scores)
For bell-shaped curves, approximately…



68% of the values have z-scores between –1 and 1.
95% of the values have z-scores between –2 and 2.
99.7% of the values have z-scores between –3 and 3.
Scores on a Final Exam
Scores on final exam have approx a bell-shaped distribution.
Mean score = 70 points and standard deviation = 10 points

Suppose Rob’s score was 2 standard devs above the mean.
What was Rob’s score?

What can you say about the proportion of students who scored
higher than Rob?
Summary of Graphical Tools
Chapter 3: Sampling
– Surveys and How to Ask Questions
Definitions:

Descriptive Statistics: Describing data using
numerical summaries (such as the mean,
IQR, etc.) and graphical summaries
(such as histograms, bar charts, etc).

Inferential Statistics: Using sample information
to make conclusions about a larger group of
items/individuals than just those in the sample.
Chapter 3: Sampling
– Surveys and How to Ask Questions
Definitions:

Population: The entire group of
items/individuals that we want information about,
about which inferences are to be made.

Sample: The smaller group, the part of the
population we actually examine in order to
gather information.

Variable: The characteristic of the items or
individuals that we want to learn about.
Basket Model
Population=
basket of balls,
1 ball for each
unit in population.
Sample =
a few balls
selected
from the
basket.
X = variable (value of
variable is recorded on
each ball as small x)
Fundamental Rule for Using Data for Inference
Available data can be used to make inferences
about a much larger group if the data can be
considered to be representative with regard
to the question(s) of interest.
In next examples … think about
the source of the data and the question of interest …
Fundamental Rule Holds?
Try It! Exercise 3.15 page 107
c. Research Question: Does a majority of adults in the
state support lowering the drinking age to 19?
Available Data: Opinions on whether or not the legal
drinking age should be lowered to 19 years old, collected
from random sample of 1000 adults in the state.
d. Research Question: same as above …
Available Data: Opinions on whether or not the legal
drinking age should be lowered to 19 years old, collected
from random sample of parents of HS students in state.
Fundamental Rule for Using Data for Inference
Try It! Exercise 3.15 Does Fundamental Rule hold?
b. Available Data: Pulse rates for smokers and
nonsmokers in a large stats class at a major university.
Research Question: Do college-age smokers have
higher pulse rates than college-age nonsmokers?
Bias: How Surveys Can Go Wrong
pg 25
Biased = method used consistently produces
values either too high or too low
Selection bias: method for selecting participants
produces sample that does not represent population.
Nonresponse bias: representative sample chosen,
but subset cannot be contacted or does not respond.
Response bias: participants respond differently from
how truly feel.
d. Magazine sends survey to random sample of
subscribers asking if would like frequency
reduced from biweekly to monthly, or would
prefer it remain same. What type of bias?
Selection
Nonresponse
Response
e. Random sample of registered voters contacted
by phone and asked whether or not going to
vote in the upcoming election. What type of
bias?
Selection
Nonresponse
Response
3.2 Margin of Error, Confidence Intervals,
and Sample Size

Sample Surveys used to estimate the proportion
of people who have a certain trait or opinion (p).

The proportion based on the sample is p̂

Quesion: how close is p̂ to p?

Measure of accuracy = margin of error … upper limit
on the amount by which sample proportion differs from
population proportion, which holds in at least 95% of all
random samples.
Margin of Error and Confidence Interval
for a population proportion p page 25

Conservative (approx 95%)
1
Margin of Error =
n
where n is the sample size.

Approx 95% Confidence Interval for p:
sample proportion 
1
n  p̂ 
1
n
Try It! Quality of Public Schools
page 26
Poll of 1,250 adults
to determine How
Americans Grade the
School System.
Quality Rating
Q: In general, how would
you rate the quality of
American public schools?
Count
Excellent
462
Pretty Good
288
Only Fair
225
Poor
225
Not Sure
50
a. What type of response variable is school quality?
b. What graph is appropriate to summarize
the distribution of this variable?
Try It! Quality of Public Schools
Poll of 1,250 adults to
determine How Americans
Grade the School System.
c. What proportion of sampled
adults rated quality as excellent?
Quality Rating
Count
Excellent
462
Pretty Good
288
Only Fair
225
Poor
225
Not Sure
50
d. What is the conservative 95% margin of error for this survey?
e. Give an approximate 95% (conservative) confidence interval
for the population proportion of adults that rate the quality of
public schools as excellent.
Try It! Quality of Public Schools -- Interpretation
Interpretation Note
Does the interval in part (e) of 34.2% to 39.8% actually
contain the population proportion of all adults that rate the
quality of public schools as excellent?
It either does or it doesn’t, but we don’t know because
we don’t know the value of the population proportion.
(And if we did know the value of p then we would not have
taken a sample of 1250 adults to try to estimate it).
The 95% confidence level tells us that in the long run,
this procedure will produce intervals that contain the
unknown population proportion p about 95% of the time.
Try It! Quality of Public Schools
Poll of 1,250 adults: How Americans Grade the School System.
f. Bonus #1: What (approximate) sample size would be
necessary to have a (conservative 95%) margin of error of 2%?
Check Table 3.1 (pg 79)
g. Bonus #2: How does the margin of error for a sample of size
1000 from a population of 30,000 compare to the margin of error
for a sample of size 1000 from a population of 100,000?
3.3 and 3.4 Sampling Methods
page 27
Good sampling designs and poor ones.
 Poor: volunteer, self-selected, convenience
samples, often biased in favor of some items
over others.
 Good: involve random selection, giving all
items a non-zero change of being selected.

Most inference methods require that the data
we have be a ________________________.
3.3 and 3.4 Sampling Methods
Random Sample = Responses are to be
independent and identically distributed (iid).

Independent = the response you will obtain from
one individual ___________________________
the response you will get from another individual.

Identically distributed = all of the responses
_______________________________________ .
3.5 Difficulties and Disasters in Sampling
3.6 How to ask Survey Questions
Asking the Uninformed (page 97)

People do not like to admit that they don’t know what
you are talking about when you ask them a question.

Crossen (Tainted Truth) gives an example:
Study of Americans’ attitudes toward various ethnic
groups, almost 30% of respondents had an opinion
about the fictional Wisians...”
Please read through these sections!
Chapter 4: Gathering Useful Data
4.1
Two Types of Research Studies

Observational Studies: The researchers simply
observe or question the participants about opinions,
behaviors, or outcomes. Participants are not asked to
do anything differently.

Experiments: The researchers manipulate something
and measure the effect of the manipulation on some
outcome of interest. Often participants are randomly
assigned to the various conditions or treatments.
Chapter 4: Gathering Useful Data

Learning of effect of one variable (called explanatory)
on another variable (called response or outcome).

Confounding variable: affects response variable
and related to explanatory variable.
Might be measured and accounted for,
or unmeasured lurking variables.
Especially a problem in observational studies.
Randomized experiments help control
the influence of confounding variables.
Try It! Student’s Health Study

Number of times a student visits Student Health Center
strongly correlated with type diet and amount weekly exercise.

Selected random sample of 100 from 3,568 students that visited
center last month; recorded number visits over prev 6 months.

Looked into records and classified each student according to
type of diet (Home-Cooked Food / Fast Food) and
amount of exercise (None / Twice a Week / Everyday).
a. Is this an observational study or a randomized experiment?
b. What are the explanatory and response variables?
Try It! External Clues Study
Study examined how external clues influence student performance.

Ugrads randomly assigned to one of four forms for midterm.
 Form 1 on blue paper, difficult questions
 Form 2 on blue paper, simple questions
 Form 3 on red paper, difficult questions
 Form 4 on red paper, simple questions

Researchers interested in impact that color and type of question
had on exam score (out of 100 points).
a. This research is based on:
an observational study
a randomized experiment
Try It! External Clues Study
Study examined how external clues influence student performance.

Ugrads randomly assigned to one of four forms for midterm.
 Form 1 on blue paper, difficult questions
 Form 2 on blue paper, simple questions
 Form 3 on red paper, difficult questions
 Form 4 on red paper, simple questions

Researchers interested in impact that color and type of question
had on exam score (out of 100 points).
b. Complete the following statements by circling.
i. Color of the paper is a(n) response
explanatory
and its type is:
ii. The exam score is a(n)
and its type is:
categorical
quantitative.
response
explanatory
categorical
quantitative.
variable
variable
Try It! External Clues Study
Study examined how external clues influence student performance.

Ugrads randomly assigned to one of four forms for midterm.

Researchers interested in impact that color and type of question
had on exam score (out of 100 points).
c. Suppose students in “blue paper” group were mostly upperclassmen and students in “red paper” group were mostly first
and second-year students. Variable “class rank” is an
example of a(n) ________________________ variable.
Q1: Most statistical inference techniques require
the data to be…
A)
B)
C)
a population.
a census.
a random sample.
Q2: When a representative sample is selected but only
a small proportion are actually able to be contacted
(after many attempts), the problem is called…
A)
B)
C)
D)
confounding.
selection bias.
nonresponse bias.
response bias.
Q3: Random sample of 1,000 college students  16%
said they had used a particular drug. An approximate
95% confidence interval for the population
proportion of all college students that have used this
particular drug is:
A)
B)
C)
D)
16% ± 3.2%
16% ± 6.4%
95% ± 3.2%
Unknown, because we don’t know
the population proportion.
Q4: 100 students were followed over a 6-month period.
The number of students who took Echinacea (herbal
supplement) and the number who developed colds
were recorded. This is an example of an …
A)
B)
Observational Study.
Experiment.
Q5: A study was conducted to compare the grade point
averages (GPAs) of male and female students
majoring in Psychology. In this study …
A)
B)
C)
D)
Gender and GPA are both response variables.
Gender and GPA are both explanatory variables.
GPA is an explanatory variable
and Gender is a response variable.
Gender is an explanatory variable
and GPA is a response variable.
SOLUTIONS:
1.
2.
3.
4.
5.
C) random sample
C) nonresponse bias
A) 16% ± 3.2%
A) Observational Study.
D) Gender is an explanatory variable
and GPA is a response variable.