* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Examples are
Survey
Document related concepts
Transcript
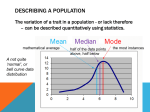
Introduction and Descriptive Statistics WHAT IS STATISTICS? STATISTICS The science of collecting, organizing, presenting, analyzing, and interpreting data to assist in making more effective decisions. Statistics is a science that helps us make better decisions in business, economics and finance as well as in other fields. Statistics teaches us how to summarize, analyze, and draw meaningful inferences from data that then lead to improve decisions. These decisions that we make help us improve the running, for example, a department, a company, the entire economy, etc. Using Statistics (Two Categories) Descriptive Statistics Collect Organize Summarize Display Analyze Inferential Statistics Predict and forecast value of population parameters Test hypothesis about value of population parameter based on sample statistic Make decisions Samples and Populations A population consists of the set of all measurements for which the investigator is interested. A sample is a subset of the measurements selected from the population. A census is a complete enumeration of every item in a population. Why Sample? Census of a population may be: Impossible Impractical Too costly Parameter Versus Statistic PARAMETER A measurable characteristic of a population. STATISTIC A measurable characteristic of a sample. Types of Data - Two Types Qualitative Categorical or Nominal: Examples are- Quantitative Measurable or Countable: Examples are- Color Temperatures Gender Salaries Nationality Number of points scored on a 100 point exam Scales of Measurement • Nominal Scale - groups or classes Gender • Ordinal Scale - order matters Ranks • (top ten videos) Interval Scale - difference or distance matters – has arbitrary zero value. Temperatures (0F, 0C), • Likert Scale Ratio Scale - Ratio matters – has a natural zero value. Salaries Population Mean For ungrouped data, the population mean is the sum of all the population values divided by the total number of population values. The sample mean is the sum of all the sample values divided by the total number of sample values. EXAMPLE: The Median MEDIAN The midpoint of the values after they have been ordered from the smallest to the largest, or the largest to the smallest. 1. 2. 3. 4. PROPERTIES OF THE MEDIAN There is a unique median for each data set. It is not affected by extremely large or small values and is therefore a valuable measure of central tendency when such values occur. It can be computed for ratio-level, interval-level, and ordinal-level data. It can be computed for an open-ended frequency distribution if the median does not lie in an open-ended class. EXAMPLES: The ages for a sample of five college students are: 21, 25, 19, 20, 22 The heights of four basketball players, in inches, are: 76, 73, 80, 75 Arranging the data in ascending order gives: Arranging the data in ascending order gives: 73, 75, 76, 80. 19, 20, 21, 22, 25. Thus the median is 21. Thus the median is 75.5 The Mode MODE The value of the observation that appears most frequently. Measures of Dispersion A measure of location, such as the mean or the median, only describes the center of the data. It is valuable from that standpoint, but it does not tell us anything about the spread of the data. For example, if your nature guide told you that the river ahead averaged 3 feet in depth, would you want to wade across on foot without additional information? Probably not. You would want to know something about the variation in the depth. A second reason for studying the dispersion in a set of data is to compare the spread in two or more distributions. RANGE MEAN DEVIATION VARIANCE AND STANDARD DEVIATION EXAMPLE – Mean Deviation EXAMPLE: The number of cappuccinos sold at the Starbucks location in the Orange Country Airport between 4 and 7 p.m. for a sample of 5 days last year were 20, 40, 50, 60, and 80. Determine the mean deviation for the number of cappuccinos sold. Step 1: Compute the mean x x n 20 40 50 60 80 50 5 Step 2: Subtract the mean (50) from each of the observations, convert to positive if difference is negative Step 3: Sum the absolute differences found in step 2 then divide by the number of observations Variance and Standard Deviation VARIANCE The arithmetic mean of the squared deviations from the mean. STANDARD DEVIATION The square root of the variance. The variance and standard deviations are nonnegative and are zero only if all observations are the same. For populations whose values are near the mean, the variance and standard deviation will be small. For populations whose values are dispersed from the mean, the population variance and standard deviation will be large. The variance overcomes the weakness of the range by using all the values in the population EXAMPLE – Population Variance and Population Standard Deviation The number of traffic citations issued during the last twelve months in Beaufort County, South Carolina, is reported below: What is the population variance? Step 1: Find the mean. x N 19 17 ... 34 10 348 29 12 12 Step 2: Find the difference between each observation and the mean, and square that difference. Step 3: Sum all the squared differences found in step 3 Step 4: Divide the sum of the squared differences by the number of items in the population. 2 ( X ) N 2 1,488 124 12 Sample Variance and Standard Deviation Where : s 2 is the sample variance X is the value of each observatio n in the sample X is the mean of the sample n is the number of observatio ns in the sample EXAMPLE The hourly wages for a sample of part-time employees at Home Depot are: $12, $20, $16, $18, and $19. What is the sample variance? The Arithmetic Mean and Standard Deviation of Grouped Data EXAMPLE: Determine the arithmetic mean vehicle selling price given in the frequency table below. EXAMPLE Compute the standard deviation of the vehicle selling prices in the frequency table below. Group Data and the Histogram Dividing data into groups or classes or intervals Groups should be: Mutually exclusive Not overlapping - every observation is assigned to only one group Exhaustive Every observation is assigned to a group Equal-width (if possible) First or last group may be open-ended Frequency Distribution Table with two columns listing: Each and every group or class or interval of values Associated frequency of each group Number of observations assigned to each group Sum of frequencies is number of observations N for population n for sample Class midpoint is the middle value of a group or class or interval Relative frequency is the percentage of total observations in each class Sum of relative frequencies = 1 Example : Frequency Distribution x Spending Class ($) 0 to less than 100 100 to less than 200 200 to less than 300 300 to less than 400 400 to less than 500 500 to less than 600 f(x) Frequency (number of customers) f(x)/n Relative Frequency 30 38 50 31 22 13 0.163 0.207 0.272 0.168 0.120 0.070 184 1.000 • Example of relative frequency: 30/184 = 0.163 • Sum of relative frequencies = 1 Cumulative Frequency Distribution x Spending Class ($) 0 to less than 100 100 to less than 200 200 to less than 300 300 to less than 400 400 to less than 500 500 to less than 600 F(x) Cumulative Frequency 30 68 118 149 171 184 F(x)/n Cumulative Relative Frequency 0.163 0.370 0.641 0.810 0.929 1.000 The cumulative frequency of each group is the sum of the frequencies of that and all preceding groups. Histogram A histogram is a chart made of bars of different heights. Widths and locations of bars correspond to widths and locations of data groupings Heights of bars correspond to frequencies or relative frequencies of data groupings Histogram Example Frequency Histogram Relative Frequency Histogram Chebyshev’s Theorem and Empirical Rule Quartiles, Deciles and Percentiles The standard deviation is the most widely used measure of dispersion. Alternative ways of describing spread of data include determining the location of values that divide a set of observations into equal parts. These measures include quartiles, deciles, and percentiles. To formalize the computational procedure, let Lp refer to the location of a desired percentile. So if we wanted to find the 33rd percentile we would use L33 and if we wanted the median, the 50th percentile, then L50. The number of observations is n, so if we want to locate the median, its position is at (n + 1)/2, or we could write this as (n + 1)(P/100), where P is the desired percentile Percentiles - Example EXAMPLE Listed below are the commissions earned last month by a sample of 15 brokers at Salomon Smith Barney’s Oakland, California, office. $2,038 $1,758 $1,940 $1,721 $2,311 $1,637 $2,054 $2,097 $2,406 $2,047 $1,471 $2,205 $1,460 $1,787 $2,287 Locate the median, the first quartile, and the third quartile for the commissions earned. Step 1: Organize the data from lowest to largest value $1,460 $2,038 $2,406 $1,471 $2,047 $1,637 $2,054 $1,721 $2,097 $1,758 $2,205 $1,787 $2,287 Step 2: Compute the first and third quartiles. Locate L25 and L75 using: 25 75 4 L75 (15 1) 12 100 100 Therefore, the first and third quartiles are located at the 4th and 12th L25 (15 1) positions, respective ly L25 $1,721 L75 $2,205 $1,940 $2,311 Measures of Variability or Dispersion Range Difference Interquartile Range Difference between maximum and minimum values between third and first quartile (Q3 - Q1) Variance Average*of Standard Deviation Square the squared deviations from the mean root of the variance Definitions of population variance and sample variance differ slightly . Skewness Another characteristic of a set of data is the shape. There are four shapes commonly observed: symmetric, positively skewed, negatively skewed, bimodal. The coefficient of skewness can range from -3 up to 3. A value near -3, indicates considerable negative skewness. A value such as 1.63 indicates moderate positive skewness. A value of 0, which will occur when the mean and median are equal, indicates the distribution is symmetrical and that there is no skewness present. The Relative Positions of the Mean, Median and the Mode Methods of Displaying Data Pie Charts Categories represented as percentages of total Bar Graphs Heights of rectangles represent group frequencies Frequency Polygons Height of line represents frequency Ogives Height of line represents cumulative frequency Time Series Plots Represents values over time • Stem-and-Leaf Displays Quick listing of all observations Conveys some of the same information as a histogram • Box Plots Median Lower and upper quartiles Maximum and minimum Pie Chart Figure 1-10: Twentysomethings split on job satisfication Category Don't like my job but it is on my career path Job is OK, but it is not on my career path Enjoy job, but it is not on my career path My job just pays the bills Happy with career 6.0% Do not like my job, but it is on my career path Happy with career 19.0% 33.0% Job OK, but it is not on my career path 19.0% Enjoy job, but it is not on my career path 23.0% My job just pays the bills Bar Chart Figure 1-11: SHIFTING GEARS Quartely net income for General Motors (in billions) 1.5 1.2 0.9 0.6 0.3 0.0 1Q 2003 2Q 3Q C4 4Q 1Q 2004 Frequency Polygon and Ogive Relative Frequency Polygon 0.3 Ogive 1.0 0.2 0.5 0.1 0.0 0.0 0 10 20 Sales 30 40 50 0 10 20 30 40 50 Sales (Cumulative frequency or relative frequency graph) Time Series Plot M o n th ly S t e e l P r o d u c t io n Millio n s o f To n s 8 .5 7 .5 6 .5 5 .5 M o n th J FMAM J J A S OND J FMAM J J A SOND J F MAM J J AS O Stem-and-Leaf Display Stem-and-leaf display is a statistical technique to present a set of data. Each numerical value is divided into two parts. The leading digit(s) becomes the stem and the trailing digit the leaf. The stems are located along the vertical axis, and the leaf values are stacked against each other along the horizontal axis. Two disadvantages to organizing the data into a frequency distribution: (1) The exact identity of each value is lost (2) Difficult to tell how the values within each class are distributed. EXAMPLE Listed in Table 4–1 is the number of 30-second radio advertising spots purchased by each of the 45 members of the Greater Buffalo Automobile Dealers Association last year. Organize the data into a stem-and-leaf display. Around what values do the number of advertising spots tend to cluster? What is the fewest number of spots purchased by a dealer? The largest number purchased? Boxplot - Example Step1: Create an appropriate scale along the horizontal axis. Step 2: Draw a box that starts at Q1 (15 minutes) and ends at Q3 (22 minutes). Inside the box we place a vertical line to represent the median (18 minutes). Step 3: Extend horizontal lines from the box out to the minimum value (13 minutes) and the maximum value (30 minutes). Box Plot – Buffalo Automobile Example – SPSS output 180 160 140 120 100 80 N= 45 NUMBERS Scatter Plots • Scatter Plots are used to identify and report any underlying relationships among pairs of data sets. • The plot consists of a scatter of points, each point representing an observation. Describing Relationship between Two Variables – Scatter Diagram Examples Describing Relationship between Two Variables – Scatter Diagram Example In the data from AutoUSA presented in the file whitner.sav, the information concerned the prices of 80 vehicles sold last month at the Whitner Autoplex lot in Raytown, Missouri. The data shown include the selling price of the vehicle as well as the age of the purchaser. Is there a relationship between the selling price of a vehicle and the age of the purchaser? Would it be reasonable to conclude that the more expensive vehicles are purchased by older buyers? Describing Relationship between Two Variables – Scatter Diagram SPSS Example Vehicle Age Vs. Selling Price 40 30 20 10 20 AGE 30 40 50 60