Download z-scores

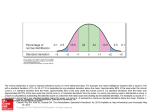
Chapter 5
Describing Data with z-scores
and the Normal Curve Model
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation


This is the most useful and
SX 36
most commonly used of the
X

6
N
6
measures of variability.
# Pancakes
The standard deviation looks to
8
find the average distance that
scores are away from the
7
mean.
9
 Conversely, the standard
3
deviation is the average
5
amount of error we would
4
expect if I used the sample
SX = 36
mean to predict every score.
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation
The
standard deviation looks to find the average
distance that scores are away from the mean.
(X – M)
8 – 6 = +2
7 – 6 = +1
7
9 – 6 = +3
9
3 – 6 = -3
3
5 – 6 = -1
5
4 – 6 = -2
4
SX = 36 S(X-M)=0
X
8
SX 36
X

6
N
6
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation
The
standard deviation looks to find the average
distance that scores are away from the mean.
(X – M)
8 – 6 = +2
7 – 6 = +1
7
9 – 6 = +3
9
3 – 6 = -3
3
5 – 6 = -1
5
4 – 6 = -2
4
SX = 36 S(X-M)=0
X
8
(X – M)2
22 = 4
12 = 1
32 = 9
(-3)2=9
(-1)2 = 1
(-2)2 = 4
S(X-M)2=28
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation
The Sums of Squares
SX 36
X

6
N
6
X
8
7
9
3
5
4
SX = 36
(X – M)
8 – 6 = +2
7 – 6 = +1
9 – 6 = +3
3 – 6 = -3
5 – 6 = -1
4 – 6 = -2
S(X-M)=0

SS   X  X
(X – M)2
22 = 4
12 = 1
32 = 9
(-3)2=9
(-1)2 = 1
(-2)2 = 4
S(X-M)2=28
  28
2
The full name for
this is the sum of
the squared
deviations from
the mean.
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation
The Variance
2
S
X
8
7
9
3
5
4
SX = 36
2
X
SS  ( X  X )
28



 4.67
N
N
6
(X – M)
8 – 6 = +2
7 – 6 = +1
9 – 6 = +3
3 – 6 = -3
5 – 6 = -1
4 – 6 = -2
S(X-M)=0
(X – M)2
22 = 4
12 = 1
32 = 9
(-3)2=9
(-1)2 = 1
(-2)2 = 4
S(X-M)2=28
The sample
variance is the
average of the
squared deviations
of the scores
around the sample
mean.
Measures of Variability
Toward a Useful Measure of Variability:
The Standard Deviation
Finally!!!
 X  X 
2
SX 
X
8
7
9
3
5
4
SX = 36
N
(X – M)
8 – 6 = +2
7 – 6 = +1
9 – 6 = +3
3 – 6 = -3
5 – 6 = -1
4 – 6 = -2
S(X-M)=0
SS

 s 2  4.67  2.16
N
(X – M)2
22 = 4
12 = 1
32 = 9
(-3)2=9
(-1)2 = 1
(-2)2 = 4
S(X-M)2=28
The standard
deviation looks to
find the average
distance that
scores are away
from the mean.
Measures of Variability
The Normal Curve and the Standard
Deviation

If we know the mean and the standard deviation of
normally distributed scores, we know a LOT of things.
The Normal Curve Model
Why is it important to know about zscores?



Because normally, raw scores are totally
meaningless.
 The best we can do is compare a raw score
to other’s raw scores.
z-scores allow us to calculate a person’s
relative standing in a distribution, relative to all
other scores.
They allow us to compare two different scores.
 We can compare apples and oranges!
The Normal Curve Model
Understanding z-scores
Converting Raw Scores to z-scores

z-scores take the mean and standard deviation of
a distribution, and use this information to produce
a numerical value to describe the location of
individual raw scores in the population distribution.
z=

or the sample distribution…..
X -
X
X 
z
SX
The Normal Curve Model
Understanding z-scores


z-scores produced from different sources can be
compared directly. If you scored a 32 on an English
test and a 73 on a Math can you compare the scores?
Not directly, but if both raw scores were converted to
z-scores, then we could.
An entire set of raw scores can be converted to zscores. The resulting distribution will have the same
shape as the original distribution, will have a mean of
0, and a standard deviation of 1.
The Normal Curve Model
Understanding z-scores
Converting z-scores to Raw Scores
z-scores
scores.

can be converted back to raw
X =  + z  X
or the sample distribution…..
X  X  z  SX
The Normal Curve Model
Understanding z-scores
Creating a z-score Distribution
z=
X -
X
60  50
z
1
10
40  50
z
 1
10
-3
-2
-1
0
1
2
3
The Normal Curve Model
Understanding z-scores
Computing Probability
Just like all probability distributions, we can compute
percentiles in this distribution by looking at the portion
of the curve falling to the left.
 A z-distribution is a special case because it has been
studied VERY much. We know ALL about it. We know
the percentile of ALL
points in the distribution.
 If we know a
persons z-score we
can compute their
percentile.

The Normal Curve Model
Understanding z-scores
Converting from Raw Scores to Percentiles
and Back Again

If we know X then:
X X
z
SX
X 
 z  score  Percentile

Look up in chart
If we know percentile then:
Find Corresponding z  score
X  X  z
Percentile  z  score 
 X
The Normal Curve Model
It’s Like Comparing Apples and Oranges



I went to the cafeteria the other day with just $1. A
piece of fruit costs exactly $1. I can buy just one
piece of fruit. I am a real bargain shopper though. I
definitely want to get the best value for my $1.
I found two pieces of fruit left, an orange that
weighs 9 ounces and an apple that weighs 9
ounces
I want to know which one is the more outstanding
fruit, which one is better value for my $1.
The Normal Curve Model
It’s Like Comparing Apples and Oranges
z
X 
X
96

 2
1.5
50%
3 oz
4.5 oz
50%
6 oz 7.5 oz
9 oz
My apple
The Normal Curve Model
It’s Like Comparing Apples and Oranges
z
X 
X
10  9

 .5
2.0
6 oz
8 oz
10 oz
My orange
12 oz
14 oz
The Normal Curve Model
It’s Like Comparing Apples and Oranges
Orange
Apple
Measures of Variability
The Normal Curve and the Standard
Deviation

If we know the mean and the standard deviation of
normally distributed scores, we know a LOT of things.
The Normal Curve Model
Why is it important to know about zscores?



Because normally, raw scores are totally
meaningless.
 The best we can do is compare a raw score
to other raw scores.
z-scores allow us to calculate a person’s
relative standing in a distribution, relative to all
other scores.
They allow us to compare two different scores.
 We can compare apples and oranges!
The Normal Curve Model
Understanding z-scores
Converting from Raw Scores to Percentiles
and Back Again

If we know X then:
X X
z
SX
X 
 z  score  Percentile

Look up in chart
If we know percentile then:
Find Corresponding z  score
X  X  z
Percentile  z  score 
 X
The Normal Curve Model
Computing Probability of a Single Score


If exam scores are normally distributed with M = 56.8
and SX = 8.14, what is the probability of selecting one
score from the population that is less than 62?
 We would first convert the raw score to a z-score.
 The question becomes, what is the probability of
achieving a z-score lower than +.64.
 We would look in the chart and find that .2389 fall
between the mean and z, another .5000 falls below
the mean, therefore such that we can say that the
raw score of 62 is at the 73.89th percentile.
However, the question was probability of a score less
than 62 which is 73.89%.
The Normal Curve Model
Computing Probability of a Single Score


If IQ scores are normally distributed with  = 100 and
 = 15, what is the probability of selecting one score
from the population that is greater than 123?
 We would first convert the raw score to a z-score.
 The question becomes, what is the probability of
achieving a z-score higher than +1.53.
 We would look in the chart and find that .4370 fall
between the mean and z, such that we can say that
the raw score of 123 is at the 93.7th percentile.
However, the question was probability, so we look at
the tail and find .0630, so that the probability of a
score of 123 or higher occurring is only 6.30%.
The Normal Curve Model
Computing Probability of a Sample Mean


If IQ scores are normally distributed with  =
100 and  = 15, what is the probability of
selecting a sample of four scores from the
population that have a mean greater than 123?
To answer this, and other similar questions, we
need to first understand the sampling
distribution of means.
The Normal Curve Model
The Sampling Distribution of Means



If we have a population of raw scores, we could
draw a sample of size 4 from it.
In fact, we could draw many samples of size 4
from it (an infinite number if you want to do this
for the rest of your life!).
If we draw many samples and compute the
means from each sample…
 then create a distribution of these means…
 we have created a sampling distribution of
means.
The Normal Curve Model
The Sampling Distribution of Means

n
94  98  104  118
4
414

 103.5
4
f
X

X
94 98 104
70
118
85
100
115
130
The Normal Curve Model
The Sampling Distribution of Means

n
87  99  103  108
87
4
397

 99.25
4
f
X

X
99
108
103
70
85
100
115
130
The Normal Curve Model
The Sampling Distribution of Means

n
52  97  106  109
4
364

 91
4
52
f
X

X
97
109
106
70
85
100
115
130
f
The Normal Curve Model
The Sampling Distribution of Means
70
85
100
115
130
The Normal Curve Model
The Sampling Distribution of Means

The sampling distribution of means will have a
mean equal to the  of the population of raw
scores.
X  X
The Normal Curve Model
The Sampling Distribution of Means

However…
X X
in fact
X X
The Normal Curve Model
The Sampling Distribution of Means

Instead, the sampling distribution of the means
will have a standard deviation (now called the
standard error of the mean, or just standard
error) that is directly related to the size of the 
of the original population and the size of the
samples in the following manner:
X 
X
n
The Normal Curve Model
The Sampling Distribution of Means

Therefore…
X
15
X 

 7.5
n
4
The Normal Curve Model
The Sampling Distribution of Means
The Central Limit Theorem

A sampling distribution is ALWAYS an
approximately normal distribution.
 It does not matter at all what shape the
distribution of raw scores looked like.
 The larger the sample size, the more normal
the distribution of sample means becomes.
The Normal Curve Model
The Sampling Distribution of Means
The Central Limit Theorem

The mean of the sampling distribution is
ALWAYS equal to the mean of the underlying
raw score population from which we create the
sampling distribution.
The Normal Curve Model
The Sampling Distribution of Means
The Central Limit Theorem


The central limit theorem states
“For any population with a mean of  and standard
deviation X, the distribution of sample means for
sample size n will have a mean of  and a standard
deviation of
X
X 
n
and will approach a normal distribution as n
approaches infinity.”
The Normal Curve Model
Computing Probability of a Sample Mean



If IQ scores are normally distributed with  =
100 and  = 15, what is the probability of
selecting a sample of four scores from the
population that have a mean greater than 123?
First we need to convert the sample mean into
a z-score.
Then we’ll need to look up the probability of the
corresponding z-score.
The Normal Curve Model
Computing Probability of a Sample Mean



First we’ll figure out the standard error.

15
X 

 7.5
n
4
Then we’ll calculate a z-score using a slightly different
formula:
X   123  100
z

 3.07
X
7.5
Then we’ll look this z-score up on the charts just like
before.
The Normal Curve Model
Computing Probability of a Sample Mean

What is probability of buying a bag of a dozen
oranges whose average weight is 9 oz or less?

Remember, oranges weigh  = 10 oz with  = 2 oz
The Normal Curve Model
Computing Probability of a Sample Mean

First we’ll figure out the standard error.

2
X 

 .577
n
12

Then we’ll calculate a z-score:
X 

9  10
z

 1.73
X
.577
Then we’ll look this z-score up on the charts.