* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 7 - 1 - Wiley
Survey
Document related concepts
Transcript
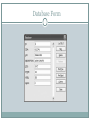
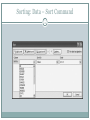
Management Science: The Art of Modeling with Spreadsheets, 3e 7-1 Chapter 7: Data Analysis for Modeling S.G. Powell K.R. Baker © John Wiley and Sons, Inc. Power Point Slides Revised By: Tony Ratcliffe, James Madison University 7-1 Data Analysis in the Context of Modeling 7-2 Supports the modeling process Improves accuracy of model Improves usefulness of conclusions Modeling is the primary goal. Data analysis is a means to that goal. Topics for Chapter 7-3 Finding facts in databases Editing, searching, sorting, filtering, and tabulating Sampling Estimating parameters Point estimates and interval estimates Finding Facts from Databases 7-4 Tables of information Each row is a record in the database. Each column is a field for the records. Excel calls such a table a list. Excel Lists 7-5 First row contains names for each field Each successive row contains one record. Lists may be: Searched and edited Sorted Filtered Tabulated Searching and Editing Lists 7-6 First assign a range name to entire list. Include column titles. With list selected Form on the Quick Access Toolbar. Examine records one at a time: Find Prev. Find Next. Enter new record with New button. Delete record with Delete button. Database Form 7-7 Criteria Button 7-8 Selected Form on the Quick Access Toolbar Allows for searching of records Enter data into a field. Click Find Next. Alternate Excel Search Techniques 7-9 Highlight entire database. Home"Editing►Find&Select►Find. Use Find and Replace to edit entries. In Find and Replace “?” stands for any single symbol “*” stands for any sequence of symbols Sorting: Data – Sort Command 710 Filtering 711 Choose Home►Editing►Sort&Filter►Filter. Will filter lists based on values Found under arrow at the title of each column Arrow on title turns blue to remind list is filtered Can remove filter by: Choose Home►Editing►Sort & Filter►Filter►Clear More Filtering 712 Top 10 option returns records with smallest or largest value of a numerical record Custom option allows filtering with compound criteria More complicated compound criteria can be achieved by clicking Custom Filter option under Number Filters or Text Filters. Tabulating 713 Select Data – Pivot Table. Creates summary tables Layout button on third step of wizard creates the format for the table Analyzing Sample Data 714 Data is unlikely to cover whole population Work with sample from population Statistics are summary measures about sample Want to construct statistics that represent population Convenience sampling Have easy access to information on subset of population Subset may not be representative Random sampling All objects in population have equal chance of appearing in sample Descriptive Statistics 715 Summarizes information in sample Gives numerical picture of observations Excel Tools – Data Analysis Descriptive Statistics table produced based on data given as input Inferential Statistics 716 Use information in sample to make inferences about population Systematic Error If sample not representative of population Avoid by careful sampling Sampling Error Sample is merely subset of population Mitigated by taking large samples Estimating Parameters: Point Estimates 717 The sample average is calculated as: x x n n i 1 The sample variance is calculated as: (xi x )2 s n 1 i 1 2 n and its square root is the sample standard deviation: n s 2 (x x ) i i 1 n 1 i (Optional) Estimating Parameters: Interval Estimates 718 We can estimate parameters in two ways, with point estimates and with interval estimates. The interval estimate approach produces a range of values in which we are fairly sure that the parameter lies, in addition to a single-value point estimate. A range of values for a parameter allows us to perform sensitivity analysis in a systematic fashion, and it provides input for tornado charts or sensitivity tables. Interval Estimates for the Mean 719 P(L <= m <= U) = 1 – a. L and U represent the lower and upper limits of the interval. 1 – a represents the confidence level. Usually a large percentage like 95 or 99% m represents the (unknown) true value of the parameter. Sampling Theory 720 Working with a population described by a Normal probability model Mean m and standard deviation s. Take repeated samples of n items from population Calculate the sample average each time The sample averages will follow a Normal distribution with a mean of m and a variance of s2/n. Estimates 721 Standard error: the standard deviation of some function being used to provide an estimate. Use the sample average to estimate the population mean. The standard deviation of the sample average is called the standard error of the mean: sx s / n Z-scores 722 The z-score measures the number of standard deviations away from the mean. The z-score corresponding to any particular sample average is: Tells how xm xm errors manyzstandard sx s n from the mean 90% of the sample averages will have z-scores between –1.64 and +1.64. The chances are 90% that the sample average will fall no more than 1.64 standard errors from the true mean. Confidence Intervals for Means 723 Upper and lower limits on estimate for mean: n>30 recommended unless original population x z(s / n ) resembles Normal z can be computed using NORMSINV(1-a/2) Replace s by the sample standard deviation s Provided that sample is larger than n = 30 Excel Descriptive Statistics also will calculate half- width of confidence interval Interval Estimates for a Proportion 724 To estimate the sample proportion p, the interval estimate is: p(1 at p) Sample size should be least 50 for this formula to pz be reliable n Sample Size Determination 725 Suppose we want to estimate mean of sample to within a range of ±R n = (zs / R)2 Assumes: Sampling from Normal distribution Known variance – can begin with small sample to estimate standard deviation Sample Size Determination for Proportions 726 Suppose want to estimate a proportion to within a range of ±R n = z2p(1 – p) / R2 Value maximized at p = 0.5 Conservative value: n = (z/2)2 / R2 Summary 727 Data collection and analysis support the modeling task where appropriate. When early sensitivity testing indicates that certain parameters must be estimated precisely, we turn to data analysis for locating relevant information and for estimating model parameters. The process of finding facts in data is aided by a facility with Excel and in particular with its database capabilities. Excel provides an array of commands for searching, sorting, filtering, and tabulating data. Excel’s Data Analysis tool for calculating descriptive statistics enables rapid construction of point estimates and interval estimates from raw data. Copyright 2011 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in section 117 of the 1976 United States Copyright Act without express permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages caused by the use of these programs or from the use of the information herein. 7 - 28