Download Determining Sample Size

Essentials of
Marketing Research
Chapter 13:
Determining Sample Size
WHAT DO STATISTICS MEAN?
• DESCRIPTIVE STATISTICS
– NUMBER OF PEOPLE
– TRENDS IN EMPLOYMENT
– DATA
• INFERENTIAL STATISTICS
– MAKE AN INFERENCE ABOUT A
POPULATION FROM A SAMPLE
POPULATION PARAMETER
VERSUS
SAMPLE STATISTICS
POPULATION PARAMETER
• VARIABLES IN A POPULATION
• MEASURED CHARACTERISTICS OF A
POPULATION
• GREEK LOWER-CASE LETTERS AS
NOTATION, e.g. m, s, etc.
SAMPLE STATISTICS
• VARIABLES IN A SAMPLE
• MEASURES COMPUTED FROM
SAMPLE DATA
• ENGLISH LETTERS FOR NOTATION
– e.g., X or S
MAKING DATA USABLE
• Data must be organized into:
– FREQUENCY DISTRIBUTIONS
– PROPORTIONS
– CENTRAL TENDENCY
• MEAN, MEDIAN, MODE
– MEASURES OF DISPERSION
• range, deviation, standard deviation, variance
Frequency Distribution of Deposits
Amount
Frequency
Percent
Probability
Under $3,000
499
16
.16
$3,000-$4,999
530
17
.17
$5,000-$9,999
562
18
.18
$10,000$14,999
718
23
.23
$15,000 or more 811
26
.26
Total
100
1
3,120
MEASURES OF CENTRAL
TENDENCY
• MEAN - ARITHMETIC AVERAGE
• MEDIAN - MIDPOINT OF THE
DISTRIBUTION
• MODE - THE VALUE THAT OCCURS
MOST OFTEN
Number of Sales Calls Per Day
by Salespersons
Salesperson
Mike
Patty
Billie
Bob
John
Frank
Chuck
Samantha
Number of
Sales calls
4
3
2
5
3
3
1
5
26
Sales for Products A and B, Both Average 200
Product A
196
198
199
199
200
200
200
201
201
201
202
202
Product B
150
160
176
181
192
200
201
202
213
224
240
261
MEASURES OF DISPERSION
• THE RANGE
• STANDARD DEVIATION
Low Dispersion Versus High
Dispersion
5
4
Low Dispersion
3
2
1
150
160
170
180
190
200
Value on Variable
210
5
4
High dispersion
3
2
1
150
160
170
180
190
Value on Variable
200
210
Standard Deviation
2
2
S=
S
=
(X - X)
n - 1
THE NORMAL DISTRIBUTION
• NORMAL CURVE
• BELL-SHAPED
• ALMOST ALL OF ITS VALUES ARE
WITHIN PLUS OR MINUS 3
STANDARD DEVIATIONS
• I.Q. IS AN EXAMPLE
NORMAL DISTRIBUTION
MEAN
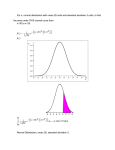
Normal Distribution
13.59%
2.14%
34.13%
34.13%
13.59%
2.14%
An example of the distribution of
Intelligence Quotient (IQ) scores
13.59%
34.13%
13.59%
34.13%
2.14%
2.14%
70
85
100
IQ
115
130
STANDARDIZED NORMAL
DISTRIBUTION
• SYMMETRICAL ABOUT ITS MEAN
• MEAN IDENTIFIES HIGHEST POINT
• INFINITE NUMBER OF CASES - A
CONTINUOUS DISTRIBUTION
• AREA UNDER CURVE HAS A PROBABILITY
DENSITY = 1.0
• MEAN OF ZERO, STANDARD DEVIATION
OF 1
A STANDARDIZED NORMAL CURVE
-2
-1
0
1
2
STANDARDIZED
SCORES
•POPULATION DISTRIBUTION
•SAMPLE DISTRIBUTION
•SAMPLING DISTRIBUTION
POPULATION DISTRIBUTION
-s
m
s
x
SAMPLE DISTRIBUTION
_
C
S
X
SAMPLING DISTRIBUTION
µX
SX

C
STANDARD ERROR
OF THE MEAN
STANDARD DEVIATION OF THE
SAMPLING DISTRIBUTION
CENTRAL LIMIT THEOREM
PARAMETER ESTIMATES
• POINT ESTIMATES
• CONFIDENCE INTERVAL ESTIMATES
RANDOM SAMPLING ERROR
AND SAMPLE SIZE ARE
RELATED
SAMPLE SIZE
• VARIANCE (STANDARD
DEVIATION)
• MAGNITUDE OF ERROR
• CONFIDENCE LEVEL
Determining Sample Size
Recap
Sample Accuracy
• How close the sample’s profile is to the true
population’s profile
• Sample size is not related to
representativeness,
• Sample size is related to accuracy
Methods of Determining Sample Size
• Compromise between what is theoretically
perfect and what is practically feasible.
• Remember, the larger the sample size, the
more costly the research.
• Why sample one more person than
necessary?
Methods of Determining Sample Size
• Arbitrary
– Rule of Thumb (ex. A sample should be at least
5% of the population to be accurate
– Not efficient or economical
• Conventional
– Follows that there is some “convention” or
number believed to be the right size
– Easy to apply, but can end up with too small or
too large of a sample
Methods of Determining Sample Size
• Cost Basis
– based on budgetary constraints
• Statistical Analysis
– certain statistical techniques require certain
number of respondents
• Confidence Interval
– theoretically the most correct method
Notion of Variability
Little
variability
Great
variability
Mean
Notion of Variability
• Standard Deviation
– approximates the average distance away from
the mean for all respondents to a specific
question
– indicates amount of variability in sample
– ex. compare a standard deviation of 500 and
1000, which exhibits more variability?
Measures of Variability
• Standard Deviation: indicates the degree of variation or
diversity in the values in such as way as to be translatable
into a normal curve distribution
• Variance = (x-x)2/ (n-1)
• With a normali curve, the midpoint (apex) of the
curve is also the mean and exactly 50% of the
distribution lies on either side of the mean.
Normal Curve and Standard
Deviation
Number of
standard
deviations
from the
mean
+/- 1.00 st dev
Percent of
area under
the curve
Percent of
area to the
right or left
68%
16%
+/- 1.64 st dev
90%
5%
+/- 1.96 st dev
95%
2.5%
+/- 2.58 st dev
99%
0.5%
Notion of Sampling Distribution
• The sampling distribution refers to what would be
found if the researcher could take many, many
independent samples
• The means for all of the samples should align
themselves in a normal bell-shaped curve
• Therefore, it is a high probability that any given
sample result will be close to but not exactly to the
population mean.
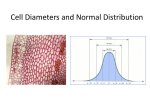
Normal, bell-shaped curve
Midpoint
(mean)
Notion of Confidence Interval
• A confidence interval defines endpoints based on
knowledge of the area under a bell-shaped curve.
• Normal curve
– 1.96 times the standard deviation theoretically defines
95% of the population
– 2.58 times the standard deviation theoretically defines
99% of the population
Notion of Confidence Interval
• Example
– Mean = 12,000 miles
– Standard Deviation = 3000 miles
• We are confident that 95% of the
respondents’ answers fall between 6,120
and 17,880 miles
12,000 + (1.96 * 3000) = 17,880
12,000 - (1.96 * 3000) = 6.120
Notion of Standard Error of a Mean
• Standard error is an indication of how far away from
the true population value a typical sample result is
expected to fall.
• Formula
– S X = s / (square root of n)
– S p = Square root of {(p*q)/ n}
•
•
•
•
•
where S p is the standard error of the percentage
p = % found in the sample and q = (100-p)
S X is the standard error of the mean
s = standard deviation of the sample
n = sample size
Computing Sample Size Using The
Confidence Interval Approach
• To compute sample size, three factors need
to be considered:
– amount of variability believed to be in the
population
– desired accuracy
– level of confidence required in your estimates
of the population values
Determining Sample Size Using a
Mean
• Formula: n = (pqz2)/e2
• Formula: n = (s2z2)/e2
• Where
– n = sample size
– z = level of confidence (indicated by the number of standard
errors associated with it)
– s = variability indicated by an estimated standard deviation
– p = estimated variability in the population
– q = (100-p)
– e = acceptable error in the sample estimate of the
population
Determining Sample Size Using a
Mean: An Example
• 95% level of confidence (1.96)
• Standard deviation of 100 (from previous
studies)
• Desired precision is 10 (+ or -)
• Therefore n = 384
– (1002 * 1.962) / 102
Practical Considerations in
Sample Size Determination
• How to estimate variability in the
population
– prior research
– experience
– intuition
• How to determine amount of precision
desired
– small samples are less accurate
– how much error can you live with?
Practical Considerations in
Sample Size Determination
• How to calculate the level of confidence
desired
– risk
– normally use either 95% or 99%
Determining Sample Size
• Higher n (sample size) needed when:
– the standard error of the estimate is high
(population has more variability in the
sampling distribution of the test statistic)
– higher precision (low degree of error) is
needed (i.e., it is important to have a very
precise estimate)
– higher level of confidence is required
• Constraints: cost and access
Notes About Sample Size
• Population size does not determine sample
size.
• What most directly affects sample size is
the variability of the characteristic in the
population.
– Example: if all population elements have the
same value of a characteristic, then we only
need a sample of one!