Download LLN, CLT - UCLA Statistics

UCLA STAT 100A
Introduction to Probability
Instructor:
Ivo Dinov,
Asst. Prof. In Statistics and Neurology
Teaching Assistants: Romeo Maciuca,
UCLA Statistics
University of California, Los Angeles, Fall 2002
http://www.stat.ucla.edu/~dinov/
STAT 100, UCLA, Ivo Dinov
Slide 1
Statistics Online Compute Resources
http://www.stat.ucla.edu/~dinov/courses_students.
dir/Applets.dir/OnlineResources.html
Interactive Normal Curve
Online Calculators for Binomial, Normal, ChiSquare, F, T, Poisson, Exponential and other
distributions
Galton's Board or Quincunx
STAT 100, UCLA, Ivo Dinov
Slide 2
Chapter 8: Limit Theorems
Parameters and Estimates
Sampling distributions of the sample mean
Central Limit Theorem (CLT)
Markov Inequality
Chebychev’s ineqiality
Weak & Strong Law of Large Numbers (LLN)
STAT 100, UCLA, Ivo Dinov
Slide 3
Basic Laws
• Markov ’ s inequality : For random variable X  0 and for a  0,
E [X]
P {X  a } 
.
a
• Chebyshev ’ s inequality : For random variable X with finite µ and  2
and for k  0,
P | X - µ |  k  
2
k
2
.
• Weak Law of Large Numbers (LLN) : For a sequence of independent
identically distribute d random variables X k , each with E [X k ]  µ  ,
 X1  X 2  ...  X n

and for   0,
P
 µ    n


 0.



n


STAT 100, UCLA, Ivo Dinov
Slide 4
Basic Laws
The first two inequalities specify loose bounds on
probabilities knowing only µ (Markov) or µ and 
(Chebyshev), when the distribution is not known.
They are also used to prove other limit results, such
as LLN.
The weak LLN provides a convenient way to
evaluate the convergence properties of estimators
such as the sample mean.
For any specific n, (X1+ X2+…+ Xn)/n is likely to
be near m. However, it may be the case that for all
k>n
(X1+ X2+…+ Xk)/k is far away from m.
Slide 5
STAT 100, UCLA, Ivo Dinov
Basic Laws
The strong LLN version of the law of large
numbers assures convergence for individual
realizations.
Strong LLN says that for any >0, with probability 1
1
X

n
k 1, n
k
µ
may be larger than  only a
finite number of times.
• Strong Law of Large Numbers (LLN) : For a sequence of
independent identically distribute d random variables X k ,
each with E [X k ]  µ  , then with probabilit y  1,
X1  X 2  ...  X n
n


 µ.



n
Slide 6
STAT 100, UCLA, Ivo Dinov
Basic Laws - Examples
The weak LLN - Based on past experience, the
mean test score is µ=70 and the variance in the
test scores is 2=10. Twenty –five students, n =25,
take the present final. Determine the probability that
the average score of the twenty –five students
will between 50 and 90.
2



 1

P
Xk  µ     1 
n
n


k

1,..,
n




 1

P
X k  70  20  
n


k 1,.., n


10
1
 0.98
25  20


Slide 7
STAT 100, UCLA, Ivo Dinov
Basic Laws - Examples
The strong LLN - Based on past experience, the
mean test score is µ=70 and the variance in the
test scores is 2=10. n=1,000 students take the
present final. Determine the probability that the
average score of the twenty –five students will
between
50 and 90.
2



 1

P
Xk  µ     1 
n
n


k

1,..,
n




 1

P
X k  70  20  
n


k 1,.., n


10
1
 0.999
1,000  20


Slide 8
STAT 100, UCLA, Ivo Dinov
Parameters and estimates
 A parameter is a numerical characteristic of a
population or distribution
 An estimate is a quantity calculated from the data to
approximate an unknown parameter
 Notation
Capital letters refer to random variables
Small letters refer to observed values
Slide 9
STAT 100, UCLA, Ivo Dinov
Questions
 What are two ways in which random observations
arise and give examples. (random sampling from finite population –
randomized scientific experiment; random process producing data.)
 What is a parameter? Give two examples of
parameters. (characteristic of the data – mean, 1st quartile, std.dev.)
 What is an estimate? How would you estimate the
parameters you described in the previous question?
 What is the distinction between an estimate (p^ value
calculated form obs’d data to approx. a parameter) and an estimator (P^
abstraction the the properties of the ransom process and the sample that produced the
estimate)
? Why is this distinction necessary? (effects of
sampling variation in P^)
Slide 10
STAT 100, UCLA, Ivo Dinov
The sample mean has a sampling distribution
Sampling batches of Scottish soldiers and taking chest
measurements. Population m = 39.8 in, and  = 2.05 in.
Sample
number
Sample
number
(a)12
12samples
samples of size
n= 66
of size
1
2
3
4
5
6
7
8
9
10
11
Chest
measurements
12
34
36
38
40
42
Chest measurement (in.)
Slide 11
44
46
STAT 100, UCLA, Ivo Dinov
Twelve samples of size 24
Sample
Sample
number
(b) 12
12 samples
= 24
samplesofofsize
sizen 24
number
1
2
3
4
5
6
7
8
9
10
11
12
Chest
measurements
34
36
38
40
42
44
Chest measurement (in.)
Slide 12
STAT 100, UCLA, Ivo Dinov
46
Histograms from 100,000 samples, n=6, 24, 100
(a) (a)
n = 6n
0.5
0.5
=6
(a) n = 6
0.0
0.037
37
1.0
38
38
39
(b) n = 24
1.0
What do we see?!?
0.5
(b) n = 24
0.0
40 37 41
42
40 38 41
39
1.0
(b) n = 24
39
42 40
41
42
39
40
41
42
0.5
0.5
0.5
0.0
0.0
1.5
37
38
39
40
0.0
37
(c) n = 100
38
39
41
37
42
38
40
41
(c) n = 100
1.0
(c) n = 100
1.5
1.5
0.5
1.0
0.0
37
1.0
40
41
38
39
0.5
Sample mean of chest measurements (in.)
42
Slide 13
42
1.Random nature of the means:
individual sample means
vary significantly
2. Increase of sample-size
decreases the variability of
the sample means!
STAT 100, UCLA, Ivo Dinov
Mean and SD of the sampling distribution
E(sample mean)
= Population mean
Population SD
SD( sample mean) =
Sample size
SD( X ) 
E( X )  E( X )  m , SD( X ) 

n
n
Slide 14
STAT 100, UCLA, Ivo Dinov
Review
 We use both x and X to refer to a sample mean. For
what purposes do we use the former and for what
purposes do we use the latter?
 What is meant by “the sampling distribution of X ”?
(sampling variation – the observed variability in the process of taking random samples;
sampling distribution – the real probability distribution of the random sampling process)
 How is the population mean of the sample average X
related to the population mean of individual
observations? (E( X ) = Population mean)
Slide 15
STAT 100, UCLA, Ivo Dinov
Review
 How is the population standard deviation of X related
to the population standard deviation of individual
observations? ( SD( X ) = (Population SD)/sqrt(sample_size) )
 What happens to the sampling distribution of X if
the sample size is increased? ( variability decreases )
 What does it mean when x is said to be an “unbiased
estimate” of m ? (E( x ) = m. Are Y^= ¼ Sum, or Z^ = ¾ Sum unbiased?)
 If you sample from a Normal distribution, what can
you say about the distribution of X ? ( Also Normal )
Slide 16
STAT 100, UCLA, Ivo Dinov
Review
 Increasing the precision of X as an estimator of m is
equivalent to doing what to SD( X )? (decreasing)
 For the sample mean calculated from a random
sample, SD( X ) =  . This implies that the
n
variability from sample to sample in the samplemeans is given by the variability of the individual
observations divided by the square root of the
sample-size. In a way, averaging decreases variability.
Slide 17
STAT 100, UCLA, Ivo Dinov
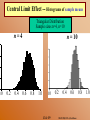
Central Limit Effect –
(a)Histograms
Triangular
of sample means
22
n=1
11
Triangular
Distribution
Y=2 X
n=2
Area = 1
0 3
(a) Triangular
0
0.0
22
0.2
0.4
2
n=1
11
0.6
0.8
1.0
0.6
0.
n=2
3
2
2
1
2
0
01
0.0
1
0.2
0.4
0.6
0.8
0
1.0 1 0.0
Sample means from sample size
n=1, n=2,
0
500 samples
0.0 0.2 0.4 0.6 0.8 1.0
0.2
0.4
0
0
0.0
Slide 18
0.2
0.4 0.6 0.8
STAT 100, UCLA, Ivo Dinov
1.0
0 0
0.2 0.40.40.6
0.60.8 0.8
1.0 1.0-- Histograms
00.0 0.2Central
0.40.6 means
0.60.8 0.81.0
0.4sample
0.0 0.00.2 0.2of
Limit
Effect
Triangular Distribution
Sample sizes n=4, n=10
n =n 4= 4
0.0 0.20.2 0.40.40.60.60.80.81.0 1.0
n =n10
= 10
5 5
4 4
3 3
2 2
1 1
0 0
0.0 0.00.2 0.20.4 0.40.6 0.60.8 0.81.0
2000.
& Sons,
Wiley
hn Wiley
& Sons,
2000.
Slide 19
STAT 100, UCLA, Ivo Dinov
Uniform Distribution
Central Limit Effect –
Histograms of sample means
2
(b) Uniform
Y=X
1
n=1
2
n=2
Area = 1
(b) Uniform
30
0.0
2
n=1
0.4
0.6
0.8
n=2
1
13
2
0
0.0 10.2
0.2
0.4
0.6
0.8
1.0
Sample means from sample size
n=1, n=2,
0
0.4 0.6 0.8 1.0
0.0 500
0.2 samples
02
0.0
0.2
0.4
0.6
0.4
0.6
0.8
1.0
1
0
0.0
Slide 20
0.2
0.8
STAT 100, UCLA, Ivo Dinov
1.0
1.0
0
0
0
Central
Limit
Effect
-Histograms
sample
0.0 of
0.2
0.4 means
0.6 1.0
0.8
0.4 0.8
0.0 0.4
0.2 0.6
0.6 1.0
0.8 1.0 0.0 0.2
0.4
0.6
0.8
0.2
Uniform Distribution
Sample sizes n=4, n=10
n = 10n = 10
n = 4n = 4
3
4
4
2
3
3
2
2
1
1
0
0.0
0
0.2
0.0 0.4
0.2 0.6
0.4 0.8
0.6 1.0
0.8
1
0
0.2
0.0 0.4
0.2 0.6
0.4 0.8
0.6 1.0
0.8
Wiley
Sons, &
2000.
© John&Wiley
Sons, 2000.
1.0
Slide 21
STAT 100, UCLA, Ivo Dinov
6
Central Limit Effect –
1.0
Histograms of sample means
0.8
(a) Exponential
Exponential Distribution

x
e , x  [0, )
0.6
0.4
n=1
1.0
n = 2Area = 1
0.2
0.80.0
(a) Exponential
0.8
0
1
2
3
4
5
6
0.6
0.6
n=1
0.8
0.4
1.0
0.2
0.8
0.2
0.0
0.6
0.00.4
0
0 0.41
0.6
2
3
4
5
6
n=1, n=2,
05001samples
2
3
0.0
4
5
1
2
3
4
3
4
0.2
0.2means from sample size
Sample
0.0
n=2
0.4
6
Slide 22
0
1
2
STAT 100, UCLA, Ivo Dinov
4 0.4
0.2 0.2
2 0.2
Histograms
of sample means
0 0.0 Central Limit Effect -- 0.0
0.0
0 0 1 12 2 3 34
0 0 1 1 2 2 3 34 45 56 6
Exponential Distribution
Sample sizes n=4, n=10
n =n4= 4
n = n10= 10
0 1.0
1.2 1.2
8 0.8
6 0.6
0.8 0.8
4 0.4
0.4 0.4
2 0.2
0 0.0
0 0
4
1
1
n Wiley & Sons, 2000.
John Wiley & Sons, 2000.
2
2
3
3
0.0 0.0
0 0
Slide 23
1
1
STAT 100, UCLA, Ivo Dinov
2
2
8
Quadratic U Distribution
Central Limit Effect –
(b)Histograms
QuadraticofUsample means
3
Y  12
(
x  12
 , x  [0,1]
2
2
n=1
n=2
Area = 1
1
(b) Quadratic U
3
2
3
2
0
0.0
0.4
0.2
n=1
0.6
0.8
1.0
n=2
1
1
0
0.0
3
0.2
0.4
0.6
0.8
1.0
0
0.0
2
1
Sample means
from sample size
n=1, n=2,
0 samples
500
1.0
n =0.04 0.2 0.4 0.6 0.8
3
0.2
0.4
0.6
0.8
1.0
2
1
1.0
Slide 24
0
0.0
0.2
n = 10
0.4
0.6
STAT 100, UCLA, Ivo Dinov
0.8
1.0
0
1
1
1
0
0
Limit
--0Histograms
sample
0.0Central
0.2 0.4
0.6 Effect
0.8 1.0
0.0 of 0.2
0.4means
0.6
0.2
0.4
0.6
0.8
1.0
0.0
0.2
0.4
0.6
0.8
0.8
1.0
Quadratic U Distribution
Sample sizes n=4, n=10
n = 10 n = 10
n = 4n = 4
3
3
3
2
2
2
1
1
1
0.2
.0 00.0
0.4
0.2
0.6
0.4 0.8
0.6 1.0
0.8
1.0
0
0.0
Slide 25
0
0.2 0.00.4 0.2
0.6 0.4
0.8 0.6
1.0
STAT 100, UCLA, Ivo Dinov
Central Limit Theorem – heuristic formulation
Central Limit Theorem:
When sampling from almost any distribution,
X is approximately Normally distributed in large samples.
CLT Applet Demo
Slide 26
STAT 100, UCLA, Ivo Dinov
Central Limit Theorem –
theoretical formulation


Let X ,X ,...,X ,... be a sequence of independent
1
2
k
observations from one specific random process. Let
and E ( X )  m and SD ( X )   and both are
n
1
finite ( 0    ; | m |  ). If X   X, sample-avg,
n
nk 1 k
Then X has a distribution which approaches
N(m, 2/n), as n   .
Slide 27
STAT 100, UCLA, Ivo Dinov
Approximate Normality in large samples
0.06
Histogram of
Bin (200, p=0.4)
probabilities with 0.04
superimposed
Normal curve
0.02
approximation.
Recall that for
0.00
Y~Bin(n,p)
60
70
80
90
100
m  E (Y )  np
Value of y
Y
  SD(Y )  np(1  p)
Y
Figure
7.3.1 theHistogram
probabilitie
For large
samples,
distributionof
ofBinomial(n=200,p=0.4)
Pˆ is approximately Normal
with
with superimposed Normal curve.
mean = p and
standard deviation =
From Chance Encounters by C.J. Wild and G.A.F. Seber, © John Wiley & Sons, 2000.
Slide 38
p(1  p)
n
STAT 100, UCLA, Ivo Dinov
Approximate Normality in large samples
Histogram of Bin (200, p=0.4) probabilities with superimposed
Normal curve approximation. Recall that for Y~Bin(n,p).
Y = # Heads in n-trials. Hence, the proportion of Heads is:
Z=Y/n.
m  E ( Z )  1 E (Y )  p
m  E (Y )  np
n
Z
Y
1
p (1  p)
  SD(Y )  np(1  p)


SD
(
Z
)

SD
(
Y
)

Y
n
n
Z
This gives us bounds on the variability of the sample proportion:
m  2SE(Z )  p  2
Z
p(1  p)
n
What is the variability of this proportion measure
over multiple surveys?
Slide 39
STAT 100, UCLA, Ivo Dinov
Approximate Normality in large samples
Histogram of
Bin (200, p=0.4)
probabilities with
superimposed
Normal curve
approximation.
Recall that for
Y~Bin(n,p)
0.06
np(1  p)  6.93
np  80.0
0.04
0.02
0.00
60
70
80
90
100
Value of y
The
sample
proportion
Y/n
be approximated by
Figure
7.3.1
Histogram
of can
Binomial(n=200,p=0.4)
probabilitie
superimposed
curve.
normal distribution,with
by CLT,
and this Normal
explains
the tight
fit between the observed histogram and a N(pn, np(1  p))
From Chance Encounters by C.J. Wild and G.A.F. Seber, © John Wiley & Sons, 2000.
Slide 40
STAT 100, UCLA, Ivo Dinov
Standard error of the sample proportion
Standard error of the sample proportion:
se( pˆ ) 
pˆ (1 pˆ )
n
Slide 41
STAT 100, UCLA, Ivo Dinov
Review
 We use both pˆ and pˆ to describe a sample proportion.
For what purposes do we use the former and for what
purposes do we use the latter? (observed values vs. RV)
 What two models were discussed in connection with
investigating the distribution of p̂? What assumptions
are made by each model? (Number of units having a property from a large
population Y~ Bin(n,p), when sample <10% of popul.; Y/n~Normal(m,s), since it’s the avg. of
all Head(1) and Tail(0) observations, when n-large).
 What is the standard deviation of a sample proportion
obtained from a binomial experiment?
SD(Y / n) 
p(1  p)
n
Slide 42
STAT 100, UCLA, Ivo Dinov
Review
 Why is the standard deviation of pˆ not useful in
practice as a measure of the precision of the estimate?
SD( Pˆ ) 
p(1  p)
, in terms of p  unknown!
n
 How did we obtain a useful measure of precision, and
what is it called? (SE( p̂ ) )
 What can we say about the true value of p and the
interval pˆ  2 SE( p̂ )? (Safe bet!)
 Under what conditions is the formula
SE( p̂ ) = pˆ (1  pˆ ) / n
applicable? (Large samples)
Slide 43
STAT 100, UCLA, Ivo Dinov
Review
 In the TV show Annual People's Choice Awards, awards are given
in many categories (including favorite TV comedy show, and favorite TV drama) and
are chosen using a Gallup poll of 5,000 Americans (US population approx.
260 million).
 At the time the 1988 Awards were screened in NZ, an NZ Listener
journalist did “a bit of a survey” and came up with a list of awards
for NZ (population 3.2 million).
 Her list differed somewhat from the U.S. list. She said, “it may be
worth noting that in both cases approximately 0.002 percent of
each country's populations were surveyed.” The reporter inferred
that because of this fact, her survey was just as reliable as the
Gallup poll. Do you agree? Justify your answer. (only 62 people surveyed, but that’s
okay. Possible bad design (not a random sample)?)
Slide 44
STAT 100, UCLA, Ivo Dinov
Review
 Are public opinion polls involving face-to-face
interviews typically simple random samples? (No! Often
there are elements of quota sampling in public opinion polls. Also, most of the time,
samples are taken at random from clusters, e.g., townships, counties, which doesn’t
always mean random sampling. Recall, however, that the size of the sample doesn’t
really matter, as long as it’s random, since sample size less than 10% of population
implies Normal approximation to Binomial is valid.)
 What approximate measure of error is commonly
quoted with poll results in the media? What poll
percentages does this level of error apply to?
( pˆ  2*SE( p̂ ) , 95%, from the Normal approximation)
Slide 45
STAT 100, UCLA, Ivo Dinov
Review
 A 1997 questionnaire investigating the opinions of
computer hackers was available on the internet for 2
months and attracted 101 responses, e.g. 82% said
that stricter criminal laws would have no effect on
their activities. Why would you have no faith that a 2
std-error interval would cover the true proportion?
(sampling errors present (self-selection), which are a lot larger than nonsampling statistical random errors).
Slide 46
STAT 100, UCLA, Ivo Dinov
Bias and Precision
 The bias in an estimator is the distance between
between the center of the sampling distribution of the
estimator and the true value of the parameter being
estimated. In math terms, bias = E (
ˆ )   , where
theta ̂ is the estimator, as a RV, of the true
(unknown) parameter  .
 Example, Why is the sample mean an unbiased
estimate for the population mean? How about ¾ of
31 n

the sample mean?
ˆ
E ()  m  E 
X m 
1 n

ˆ

E ()  m  E   X   m  0
nk 1 k 
4n 


k 1 k 
3
m
m  m   0, in general.
4
4
Slide 47
STAT 100, UCLA, Ivo Dinov
Bias and Precision
 The precision of an estimator is a measure of how
variable is the estimator in repeated sampling.
value of parameter
value of parameter
(a) No bias, high precision
(b) No bias, low precision
value of parameter
value of parameter
(c) Biased, high precision
(d) Biased, low precision
Slide 48
STAT 100, UCLA, Ivo Dinov
Standard error of an estimate
The standard error of any estimate ˆ [denoted se( ˆ )]
• estimates the variability of ˆ values in repeated
sampling and
• is a measure of the precision of ˆ .
Slide 49
STAT 100, UCLA, Ivo Dinov
Review
 What is meant by the terms parameter and estimate.
 Is an estimator a RV?
 What is statistical inference? (process of making conclusions or
making useful statements about unknown distribution parameters based on
observed data.)
 What are bias and precision?
 What is meant when an estimate of an unknown
parameter is described as unbiased?
Slide 50
STAT 100, UCLA, Ivo Dinov