* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Statistics 400
Psychometrics wikipedia , lookup
Foundations of statistics wikipedia , lookup
Degrees of freedom (statistics) wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
History of statistics wikipedia , lookup
Taylor's law wikipedia , lookup
Omnibus test wikipedia , lookup
Resampling (statistics) wikipedia , lookup
Misuse of statistics wikipedia , lookup
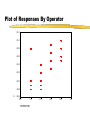
Statistics 400 - Lecture 16 Last Day: Two-Sample T-test (10.2 and 10.3) Today: Comparison of Several Treatments (14.1-14.3) Last day, we looked at comparing means for two treatments When more than two treatments are being compared, we will use a statistical technique call the Analysis of Variance (ANOVA) The same underlying assumptions apply in the ANOVA situation a the two independent samples case Example (Pulp Mill) An important measure of performance at pulp mills is based on pulp brightness measured by a reflectance meter An investigation was performed (Sheldon, 1960; Industrial and Engineering Chemistry ) to investigate if there is a difference in product quality for different mill operators Want to see if there are differences in the reflectance for different operators Data: A 59.8 60.0 60.8 60.8 59.8 Operator B C 59.8 60.7 60.2 60.7 60.4 60.5 59.9 60.9 60.0 60.3 D 61.0 60.8 60.6 60.5 60.5 ANOVA Situation Situation: Have k independent random samples Each sample comes from a normal population The population standard deviations are equal Want to test test a hypothesis about the equality of the population means Structure of Data Have k independent random samples from k populations…sample size from each pop. may be different Denote jth observation from the ith population as yij Population 1 y11 y12 . . . y1n1 Population 2 y21 y12 . . . y2n2 … Population k yk1 yk2 . . . yk,nk Estimating 2 Have assumed that data from each population comes from independent normal distributions with equal standard deviations (variances) That is, yij has a N (i , ) distribution If we wanted to estimate based on the data from only 1 population, we would use 2 Combining the data from all of the populations: Another estimate for 2 Why are we doing this? What is the null hypothesis we have in mind? Suppose H0 is true, how could we estimate the mean? Variance about true mean: When the null hypothesis is true, we expect When it is false Potential Test Statistic More Formal Approach Model for comparing k treatments: Yij i eij for i =1, 2, …, k and j =1, 2, …, ni where i is the ith population mean and eij had a N (0, ) distribution Want to test: H 0 : 1 2 ... k Sum of Squares for treatment Sum of Squares for Error (residual) Total Sum of Squares Degrees of freedom Mean Squares Test Statistic Hypotheses P-value ANOVA Table: Example (Pulp Mill): Data: A 59.8 60.0 60.8 60.8 59.8 Operator B C 59.8 60.7 60.2 60.7 60.4 60.5 59.9 60.9 60.0 60.3 D 61.0 60.8 60.6 60.5 60.5 Summary Statistics: OPERATOR 1.00 2.00 3.00 4.00 Y Y Y Y Count 5 5 5 5 Mean Std Deviation 60.26 .50 60.06 .24 60.62 .23 60.68 .22 Plot of Responses By Operator 61.2 61.0 60.8 60.6 60.4 60.2 60.0 Y 59.8 59.6 0.0 1.0 OPERATOR 2.0 3.0 4.0 5.0 ANOVA Table O Y m e d u F i a g f B 9 3 6 1 1 W 0 6 1 T 9 9