* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ankenman`s Statistics Lecture Slides
Survey
Document related concepts
Transcript
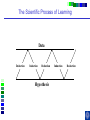
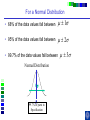
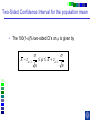
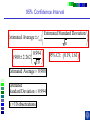
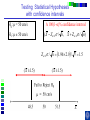
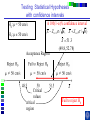
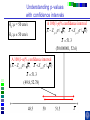
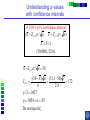
IE 407 Statistics Review Professor Bruce Ankenman Winter 2010 [email protected] The Scientific Process of Learning Data Deduction Induction Deduction Hypothesis Induction Deduction Induction and Deduction • Induction - Knowing how a particular instance works and arguing to a general principle • Deduction - Knowing a general principle and arguing to a particular instance What is Statistics? • A science of collecting and analyzing data for the purpose of drawing conclusions and making decisions. • An integral part of the scientific method. • Provides data collection methods to reduce biases, and analysis methods to identify patterns and draw inferences from noisy data. (The key feature of any data is that they are variable.) Relationship between Probability and Statistics Probability Population Sample Statistics • A population is a collection of all units of interest. • A sample is a subset of a population that is actually observed. • In probability (assumes that population and its parameters are known), we proceed from the general to a particular. • In statistics (assumes that population and its parameters are unknown), we proceed from a particular to the general. • Thus, probability is deductive and statistics is inductive in nature. Other Key Terms • Variable: measurable property or attribute associated with each unit in the population (e.g. employment status) • Parameter: numerical value of a characteristic for the population (e.g. unemployment rate) • Statistic: numerical value calculated from the sample data that is used as an estimate of a population parameter Phases in Statistical Analysis • Data Collection: The process of collecting data from samples surveys, observational studies and designed experiments • Data Analysis: Descriptive statistical studies (plotting and summarizing key features of the data) to discover major and patterns in the data • Statistical Inference: Drawing inferences and making decisions based on the data. What questions can Statistics answer? • Product development: What combination of manufacturing processes (raw material, temperature, pressure…) leads to the best product. In making a commercial, what techniques will work? What makes a commercial that consumers will remember? • Quality Assurance: Inspections of finished products Sampling the products as they are being produced • Changes in a system over time: Is a production process remaining in control? Is the number of female students studying engineering increasing? Variation in the Process • There will almost always be variation in any process. • Our goal is to learn about the process, so that we can improve it. • Information is just variation that has a pattern. Always PLOT the Data first. Plot vs Time Plot vs Time 1000 160 900 140 800 120 700 100 Data Data 600 500 400 80 60 300 40 200 20 100 0 0 0 5 10 15 20 0 25 5 10 15 20 25 Tim e Tim e Plot vs Time Data Plot 250 130 120 200 150 100 Data Data 110 90 100 80 50 70 60 0 0 1 2 Type 3 0 5 10 15 Tim e 20 25 Statistics for Summarizing Numerical Data • Measures of Location A statistic that represents a central or typical value in the data. • Measures of Dispersion Two data sets may have the same center but quite different dispersions (spread) around it. Measures of Location • Sample mean (average) Most commonly used sensitive to extreme values Measures of Location • Median: • Arrange data from small to large (x(1), x(2), . . . x(n)) x [ n1] for n is odd: median = for n is even: median = 2 x [ n 2 ] x [ n 21] 2 not sensitive to extreme values (robust) Measures of Location • Mode: value that occurs most often • Population mean (True mean): m for a finite population of size N: N m x i 1 N i Example Age of faculties in a department (made up) 25, 27, 41, 43, 46, 46, 47, 48, 49, 49, 51, 52, 52, 52, 55, 61, 70. Mean: (25 + 27 + 41 + …+ 70) / 17 = 47.88 Mode: 52 Median: 49 Shape of a Distribution • Symmetrical mean = mode = median • Skewed to the right mean > median > mode • Skewed to the left mode > median > mean Measure of Dispersion • Population Variance: 2 N 2 2 ( x m ) i i 1 N • Population Standard Deviation is the squared root of the population variance Measure of Dispersion • Sample variance: Measure of Dispersion • Quartiles: Division points where data is divided into 4 equal parts first (lower) quartile has 25% data points below and 75% above it second quartile (median) has 50% below and above it third (upper) quartile has 75% below and 25% above it pth percentile has p percent of the data points below it and (1p%) above it Measure of Dispersion • Inter quartile Range (IQR): IQR = Q3 - Q1 • Range Maximum – Minimum • Coefficient of Variation s x Notation Parameter Estimator Mean m x Median m~ ~ x (Statistic) Variance s Stnd. Dev. s Total number n 2 How do we find out about the properties of an estimator? • We need to know about Sampling Distribution: the actual probability distribution that you would get if you sampled a statistic an infinite number of times from the same population. The estimator is a function of the data. Each observation of data is a random variable drawn from a distribution. Usually we assume that all observations in the sample are independent and come from the same distribution. (I.I.D. Independent, Identically Distributed). We use plots to verify this and to see the general characteristics of the distribution. Run charts of the data can help to determine if the data are independent and identically distributed. Run charts to test IID assumptions Plot vs Time Plot vs Time 160 250 140 200 120 150 Data Data 100 80 100 60 40 50 20 0 0 5 10 15 Tim e 20 25 0 0 5 10 15 Tim e 20 25 Normal Distribution For a Normal Distribution • 68% of the data values fall between m 1 • 95% of the data values fall between m 2 • 99.7% of the data values fall between Normal Distribution 6 m 99.7% of parts in Specification m 3 Standard Normal Distribution Histograms to test Normal assumptions Example 1 • Let X denote the resistance of a random selected resistor. Suppose that X ~N(m= 4.3, = 0.6557). • If the specification limits are 3 to 8 ohms, what fraction of the resistors conform to the specifications? Percentage Out of Specification 0.6557 ZL=How many ’s? % defective Z L ZU 2.39% 0% LSL=3 USL=8 ZU=How many ’s? m 4.3 Normal Distribution LSL-m -(USL-m ) 3-4.3 -(8-4.3) 0.6557 0.6557 1.98 5.64 .0239 0 2.39% Using the z-Table z CDF of Standard Normal (mean 0, Stdev 1) z z z -1.90 0.09 0.08 0.07 f(-1.98) f(-1.97) 0 0.06 0.05 0.04 0.03 0.02 0.01 0.00 Example 2 • Assume that test scores follow a normal distribution with mean 500 and standard deviation 100. That is, if we use X to denote the test score of an individual, X ~N(m= 500, = 100). • What has to be your score to be sure that you are among the top 10%? 1.28 ’s 1.28 0.90 500 1.28100 628 10% Above 628 is in the top 10% m 500 628 • How well have you done compared to the others if your score is 750? (750 500) /100 2.5 750 is in the top 1%. 2.5 0.99 Example 3 • A manufacturer of potato chips claims that the average contents of bags sold weighs 12 ounces. The distribution is known to be normal with standard deviation =0.4 ounces. A random sample of 16 bags produced a sample mean weight of 11.84 ounces. Is it reasonable to say that the average is 12? Linear Combinations of Random Variables • Suppose X and Y are independent r.v.’s with means mx and my and variances x2 and y2 (a, b,c,and d are scalars), then W=(aX+b) +( cY +d) V(W) = a2 x2+ c2 y2 E(W) = amx +b+ cmy+d If X and Y are Normal then W is Normal. Example (Sample Mean) • The individuals are Normally distributed, so X n x i 1 i /n is Normally distributed. With expected value m. With variance /n Example (Sample Mean) • The individuals are Normally distributed, so X m z / n has the standard Normal distribution. 95% -1.96 1.96 If we keep taking samples of 16 and calculating the sample mean: • 95% of the time the interval will contain the true value: .95 P X 1.96 m X 1.96 n n • “The probability is .95 that the random interval will include m.” X 1.96 n Confidence Interval Estimation • A 100(1-a)% confidence interval (CI) for an unknown parameter q is a random interval [L,U] computed from sample data that will contain the true q with probability 1-a. This probability is called the confidence level. PL q U 1 a Two-Sided Confidence Interval for the population mean • The 100(1-a)% two-sided CI’s on m is given by X za / 2 n m X za / 2 n The confidence interval gives us possible values for the population mean. • Use 95% confidence .4 .4 11.84 1.96 m 11.84 1.96 16 16 11.64 m 12.04 • So it is reasonable to think that the mean is 12, but it could be as low as 11.64. What if we have to estimate the standard deviation? (i.e. s=0.4) The confidence interval needs to be bigger to account for the fact that we don’t really know the variance. X za / 2 n m X za / 2 n s s .95 P X t0.025,n1 m X t0.025, n1 n n z distribution t distribution -t0.025,n-1 -1.96 95% 95% 1.96 t0.025,n-1 Properties of t-distribution • Let tv denote the density function curve for v degrees of freedom Each tv curve is bell-shaped and centered at 0. Each tv curve is more spread out than the standard normal (z) curve. As v increases, the spread of the corresponding tv curve decreases. As v goes to infinity, the tv distribution approaches the standard normal distribution. t critical value • ta,v: the number on the measurement axis for which the area under the t curve with v degrees of freedom to the right of ta,v is a. CI’s on population mean (variance estimated by n-1 degrees of freedom) (Two-Sided CI): X ta / 2,n 1 s n m X ta / 2,n 1 s n • Use 95% confidence, a=0.05, n=16 t0.025,n 1 2.131 11.84 2.131 .4 m 11.84 2.131 16 11.63 m 12.05 .4 16 • So it is reasonable to think that the mean is 12, but it could be as low as 11.63. Interpreting Confidence Intervals There is a big difference between Statistically Significant and Practically Important. Always look at both sides of the confidence interval and think about how the value would affect your decision. • Average time saved by driving by the “Shortcut” (-.5,1) minutes. • Average amount of money saved by buying from Amazon.com (5,7) dollars. • Average weight of gold in a pound of Lake Michigan Sand (0,5) grams. • Average error on yard markers on a football field (.02, .04) inches. Calculating and interpreting a confidence interval for a difference between 2 design alternatives. Could each of you rate a couple of designs that we have sketched to fulfill your need? Rate these two designs on a scale from 1-10, where 10 means it throws the ball, straight and as far as possible using the specified rubber band. Raw Data and Plot of Data Person Slingshot Catapult 1 5 6 2 4 7 3 6 7 4 8 9 5 7 8 6 9 9 7 4 5 8 7 6 9 7 8 10 5 6 Ave 6.200 7.100 Stdev 1.687 1.370 Diff 1 System Design 103 91 81 7 1 6 0 5 1 4 -1 3 21 11 0 0.900 0.994 Slingshot Catapult Data and Better Plot – Look at Differences (Difference = Catapult – Slingshot) Person Slingshot Catapult 1 5 6 2 4 7 3 6 7 4 8 9 5 7 8 6 9 9 7 4 5 8 7 6 9 7 8 10 5 6 Ave 6.200 7.100 Stdev 1.687 1.370 Diff 1 3 1 1 1 0 1 -1 1 1 0.900 0.994 Comparison Plot Slingshot Catapult 10 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 Person 7 8 9 10 A Histogram of the Differences Diff 1 3 1 1 1 0 1 -1 1 1 0.900 0.994 Mean = 0.900 StDev = 0.994 Histogram of Difference -2 0 -1 1 8 7 0 1 6 Number of Responses Person Slingshot Catapult 1 5 6 2 4 7 3 6 7 4 8 9 5 7 8 6 9 9 7 4 5 8 7 6 9 7 8 10 5 6 Ave 6.200 7.100 Stdev 1.687 1.370 1 7 5 2 0 4 3 1 3 4 0 2 5 0 1 0 -2 -1 0 1 2 Rating Difference 3 4 5 “Is the average difference between the two design ratings significantly different than zero?” Our estimate of the average difference between the two ratings is 0.9 ± ?? We will create a confidence interval that, with 95% confidence, contains the true average difference in the ratings if we were to ask all people in the target audience. 95% Confidence Interval Estimated Standard Deviation Estimated Average tn -1 n 0.994 95% CI: 0.900 2.262 10 Estimated Average 0.900 Estimated Standard Deviation 0.994 n 10 observations 0.19, 1.61 Show Spreadsheet 95% Confidence Interval, (0.19, 1.61) Statistical Significance: Is zero outside of the CI? Yes, zero is outside the CI so we are 95% confident that the catapult has a higher average rating than the slingshot because all the numbers in the confidence interval are positive. Practical Importance: Does either end of the CI have a difference that really matters to the application? On average, the Catapult could be as much as 1.61 rating points better than the Slingshot, but it may be as little as 0.19 points better. Would the difference matter to you if it was 0.19? No. 1.61? Yes. Statistically Significant -vs- Practically Important Assume a difference of 1.0 is important. Stat.Sign Pract.Imp. No (CI includes 0) Yes (0 is outside CI) No, to both ends. Even if there is a difference, it doesn’t matter. (-0.2, 0.2) There is a difference, but it doesn’t matter. (0.1, 0.2) Yes, to one end of the CI. We need more data, to find out if there really is any difference. (-0.2, 1.5) There is a difference, we might want more data to be sure it matters. (0.2, 1.5) Yes, to both ends. We need a lot more data. (-2.0, 2.0) There is a clear difference that matters. (1.0, 1.5) Show Spreadsheet with Estimate of Number needed Normal Assumption • If we assume that each xi is normally distributed, then the sample mean is a linear combination of Normally distributed random variables and thus it has a Normal distribution. • If this is a good assumption, we have a complete description of the sampling distribution for the sample mean. N(m,2/n) • What if that is a bad assumption? Central Limit Theorem (C.L.T.) • If X1, X2, …, Xn is a random sample of size n taken from population with mean m and variance 2, and if X is the sample mean, then the limiting form of the distribution of X m z / n as n is the standard normal distribution. “For sufficiently large n, the sample mean has an approximately normal distribution, the larger the sample, the better the approximation.” 50 Random Draws from a Uniform (0-10) Frequency 10 Uniform (0-10) 5 0 0 2 4 6 C51 8 10 100 Means of 50 Random samples from a Uniform (0-10) Frequency 20 Mean of 50 random sample from (0-10) 10 0 4 .0 0 4 .2 5 4 .5 0 4 .7 5 5 .0 0 5 .2 5 5 .5 0 5 .7 5 6 .0 0 C52 Summary If n is large OR The individuals are Normally distributed then 2 X ~ N m , n and X m z / n is the standard Normal distribution. When n is large • The assumptions that the sample is drawn from a normal population and the variance is known can be relaxed. CLT allows us to regard the distribution of the sample mean as N(m,2/n). The sample variance s2 can be regarded as an accurate estimator of 2. Hypothesis testing • Statistical hypothesis: Statements about the parameters of 1 or more populations. • Null hypothesis: ( H0) Statement being tested usually, “no effect” or “no difference” • Alternative hypothesis: (HA or H1) statement you hope or expect to be true can be one sided if no specific idea, use two sided. Null and Alternate Hypotheses • Hypothesis: a statement of a theory or a claim. • Recall that we want to assess the validity of a claim against a counterclaim using sample data. • The two competing claims must be mutually exclusive and collectively exhaustive: Null Hypothesis (H0): the standard or favored claim. Alternate Hypothesis (HA): the claim to be proved. • Begin with the assumption that H0 is true. • If the data fail to contradict H0, then H0 is not rejected. • The proof of HA is by contradiction of H0. Failing to reject H0 means that H0 cannot be ruled out as a possible explanation for the observed data (i.e., failing to reject H0 does not mean that we accept it as true). Only when the data STRONGLY contradict H0, it is rejected and HA is accepted. Examples • Is the average tube diameter being produced different from the standard 3mm? • Does adding compound X increase the average yield of the process? • Is the average SAT scores of UC students the same as NU students? Note • Hypotheses are about parameters of the population, not about the sample. • H0 is always stated as equality. • We either reject or do not reject the null hypothesis. The rejection of the null hypothesis implies the acceptance of the alternative hypothesis. General steps for Hypothesis testing • From the problem context, identify the parameter of interest. • State the null hypothesis, H0 involving an equality for the parameter of interest. • Specify an appropriate alternative hypothesis, H1. • Choose a significance level a. • Compute a 100(1-a)% confidence interval for the parameter of interest. • H0 should be rejected based on whether the confidence interval contains the hypothesized value in H0. (This is statistical significance) • (Decisions should be made based on the practical importance not just the statistical significance.) Hypothesis testing on the mean - 2 known Aircrew escape systems are powered by a solid propellant. Specifications require that the mean burning rate must be 50 cm/s. We know the standard deviation of burning rate is = 2.0 cm/s. The experimenter decides to specify the significance level at a = 0.05. He selects a random sample of n = 7 and obtains a sample average burning rate 51.3 cm/s. What conclusion should be drawn? Testing Statistical Hypotheses with confidence intervals H0: m = 50 cm/s A 100(1-a)% confidence interval H1: m 50 cm/s ( X Za / 2 / n , X Za / 2 / n ) Za / 2 / n 1.96 2.0 / 7 1.5 ( X 1.5) ( X 1.5) X Testing Statistical Hypotheses with confidence intervals H0: m = 50 cm/s H1: m 50 cm/s A 100(1-a)% confidence interval ( X Za / 2 / n , X Za / 2 / n ) X 51.3 (49.8, 52.78) Acceptance Region Critical values critical region X Fail to reject H0 Usual Method of Hypothesis testing - two sided To test: H0 : m = m0 H1: m m0 Rejection Acceptance Region Region Rejection Region N (0,1) a /2 za / 2 a /2 0 za / 2 X m0 Compute: Z 0 which has a N(0,1) if H0 is true. / n za / 2 Z 0 za / 2 Fail to reject H0 if X m0 51.3 50 Z0 1.72 1.96 / n 2.0 / 7 Fail to reject H0 Same as m0 za / 2 / n X m0 za / 2 / n Type I error Type I error - reject H0 when it is actually true. Accept H0 Reject H0 Reject H0 m0 a = P(Type I error) = P(reject H0 when it is true) - a: significant level of the test. - 1 - a : confidence level of the test Type II error Type II error - fail to reject H0 when it is false. b = P(Type II error) = P( fail to reject H0 when it is false) We need to have a particular alternative to find b. Distribution of x if m A 52 Normal Distribution Type II error b = P(Type II error if m=52 and n=7) = P( fail to reject H0 when it is false) P(48.5 X 51.5 given m 52 and 2.0 7) How many standard deviations? Note that standard deviation of x is / 48.5 51.5 m A 52 n Type II error b = P(Type II error if m=52 and n=7) = P( fail to reject H0 when it is false) P( X 51.5 given m 52) P(Type II error if m A is 52) upper rejection region boundary-m A lower rejection region boundary-m A / n / n 51.5 52 48.5 52 2.0 / 7 2.0 / 7 0.6614 4.630 0.2549 0 25% Power of a test • Power of a test Probability of correctly rejecting a false null hypotheses A measure of the sensitivity of the test • Power of a test = 1 - P(Type II error) = 1 - b P(Type II error if m is 52) 0.25 Power of the test if m A is 52) 1- 0.25 0.75 • In general, if you decrease a, Type I error, then b, Type II error will increase unless you increase sample size. p- value • p - value The probability that the test statistic will take on a value as extreme as the observed value when H0 is true. The smallest level of significance, a, that would lead to rejection of the H0. If p-value < a, reject H0. If p-value > a, do not reject H0. Understanding p-values with confidence intervals H0: m = 50 cm/s H1: m 50 cm/s A 100(1-p)% confidence interval ( X Z p / 2 / n , X Z p / 2 / n ) X 51.3 (50.000001, 52.6) A 100(1-a)% confidence interval ( X Za / 2 / n , X Za / 2 / n ) X 51.3 (49.8, 52.78) X Understanding p-values with confidence intervals A 100(1-p)% confidence interval ( X Z p / 2 / n , X Z p / 2 / n ) X 51.3 (50.0001, 52.6) X Z p / 2 / n 50 (50 X ) n (51.3 50) 7 1.72 2.0 p / 2 .0427 p .0854 a .05 Do not reject H 0 Z p/2