Download Ankenman`s Statistics Lecture Slides

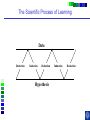
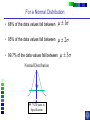
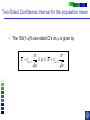
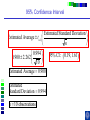
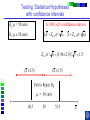
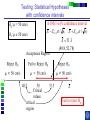
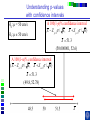
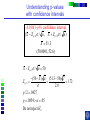
IE 407 Statistics Review
Professor Bruce Ankenman
Winter 2010
[email protected]
The Scientific Process of Learning
Data
Deduction
Induction
Deduction
Hypothesis
Induction
Deduction
Induction and Deduction
• Induction - Knowing how a particular instance works and
arguing to a general principle
• Deduction - Knowing a general principle and arguing to a
particular instance
What is Statistics?
• A science of collecting and analyzing data for the
purpose of drawing conclusions and making
decisions.
• An integral part of the scientific method.
• Provides data collection methods to reduce biases,
and analysis methods to identify patterns and draw
inferences from noisy data. (The key feature of any
data is that they are variable.)
Relationship between Probability and Statistics
Probability
Population
Sample
Statistics
• A population is a collection of all units of interest.
• A sample is a subset of a population that is actually observed.
• In probability (assumes that population and its parameters are
known), we proceed from the general to a particular.
• In statistics (assumes that population and its parameters are
unknown), we proceed from a particular to the general.
• Thus, probability is deductive and statistics is inductive in nature.
Other Key Terms
• Variable: measurable property or attribute associated
with each unit in the population (e.g. employment
status)
• Parameter: numerical value of a characteristic for the
population (e.g. unemployment rate)
• Statistic: numerical value calculated from the sample
data that is used as an estimate of a population
parameter
Phases in Statistical Analysis
• Data Collection: The process of collecting data from
samples surveys, observational studies and
designed experiments
• Data Analysis: Descriptive statistical studies
(plotting and summarizing key features of the data) to
discover major and patterns in the data
• Statistical Inference: Drawing inferences and
making decisions based on the data.
What questions can Statistics answer?
• Product development:
 What combination of manufacturing processes (raw material,
temperature, pressure…) leads to the best product.
 In making a commercial, what techniques will work? What
makes a commercial that consumers will remember?
• Quality Assurance:
 Inspections of finished products
 Sampling the products as they are being produced
• Changes in a system over time:
 Is a production process remaining in control?
 Is the number of female students studying engineering
increasing?
Variation in the Process
• There will almost always be variation in any
process.
• Our goal is to learn about the process, so that we
can improve it.
• Information is just variation that has a pattern.
Always PLOT the Data first.
Plot vs Time
Plot vs Time
1000
160
900
140
800
120
700
100
Data
Data
600
500
400
80
60
300
40
200
20
100
0
0
0
5
10
15
20
0
25
5
10
15
20
25
Tim e
Tim e
Plot vs Time
Data Plot
250
130
120
200
150
100
Data
Data
110
90
100
80
50
70
60
0
0
1
2
Type
3
0
5
10
15
Tim e
20
25
Statistics for Summarizing Numerical Data
• Measures of Location
 A statistic that represents a central or typical value in
the data.
• Measures of Dispersion
 Two data sets may have the same center but quite
different dispersions (spread) around it.
Measures of Location
• Sample mean (average)
 Most commonly used
 sensitive to extreme values
Measures of Location
• Median:
• Arrange data from small to large (x(1), x(2), . . . x(n))
x [ n1] 
 for n is odd: median =



 for n is even: median =
2 
x [ n 2 ]   x [ n 21] 
2
 not sensitive to extreme values (robust)
Measures of Location
• Mode: value that occurs most often
• Population mean (True mean): m for a finite population of
size N:
N
m 
x
i 1
N
i
Example
Age of faculties in a department (made up)
25, 27, 41, 43, 46, 46, 47, 48, 49, 49, 51, 52, 52, 52,
55, 61, 70.
Mean: (25 + 27 + 41 + …+ 70) / 17 = 47.88
Mode: 52
Median: 49
Shape of a Distribution
• Symmetrical
mean = mode = median
• Skewed to the right
mean > median > mode
• Skewed to the left
mode > median > mean
Measure of Dispersion
• Population Variance:

2
N
2 
2
(
x

m
)
 i
i 1
N
• Population Standard Deviation is the squared root of the
population variance
Measure of Dispersion
• Sample variance:
Measure of Dispersion
• Quartiles: Division points where data is divided into 4
equal parts
 first (lower) quartile has 25% data points below and 75%
above it
 second quartile (median) has 50% below and above it
 third (upper) quartile has 75% below and 25% above it
 pth percentile has p percent of the data points below it and (1p%) above it
Measure of Dispersion
• Inter quartile Range (IQR):
IQR = Q3 - Q1
• Range
Maximum – Minimum
• Coefficient of Variation
s
x
Notation
Parameter
Estimator
Mean
m
x
Median
m~
~
x

(Statistic)
Variance

s
Stnd. Dev.

s
Total number

n
2
How do we find out about the properties of an estimator?
• We need to know about
 Sampling Distribution: the actual probability distribution that
you would get if you sampled a statistic an infinite number of
times from the same population.
 The estimator is a function of the data.
 Each observation of data is a random variable drawn from a
distribution. Usually we assume that all observations in the
sample are independent and come from the same distribution.
(I.I.D. Independent, Identically Distributed).
 We use plots to verify this and to see the general characteristics
of the distribution.
 Run charts of the data can help to determine if the data are independent and
identically distributed.
Run charts to test IID assumptions
Plot vs Time
Plot vs Time
160
250
140
200
120
150
Data
Data
100
80
100
60
40
50
20
0
0
5
10
15
Tim e
20
25
0
0
5
10
15
Tim e
20
25
Normal Distribution
For a Normal Distribution
• 68% of the data values fall between
m  1
• 95% of the data values fall between
m  2
• 99.7% of the data values fall between
Normal Distribution
6
m
99.7% of parts in
Specification
m  3
Standard Normal Distribution
Histograms to test Normal assumptions
Example 1
• Let X denote the resistance of a random selected
resistor. Suppose that X ~N(m= 4.3,  = 0.6557).
• If the specification limits are 3 to 8 ohms, what fraction of
the resistors conform to the specifications?
Percentage Out of Specification
  0.6557
ZL=How many ’s?
% defective    Z L      ZU 
2.39%
0%
LSL=3
USL=8
ZU=How many ’s?
m  4.3
Normal Distribution
 LSL-m 
 -(USL-m ) 
 






  


 3-4.3 
 -(8-4.3) 
 





 0.6557 
 0.6557 
   1.98     5.64 
 .0239  0
 2.39%
Using the z-Table
z   CDF of Standard Normal (mean  0, Stdev  1)
 z 
z
z
-1.90
0.09
0.08
0.07
f(-1.98)
f(-1.97)
0
0.06
0.05
0.04
0.03
0.02
0.01
0.00
Example 2
• Assume that test scores follow a normal distribution with mean
500 and standard deviation 100. That is, if we use X to denote
the test score of an individual, X ~N(m= 500,  = 100).
• What has to be your score to be sure that you are among the top
10%?
1.28 ’s
 1.28  0.90
500 1.28100  628
10%
 Above 628 is in the top 10%
m  500 628
• How well have you done compared to the others if your score is
750?
(750  500) /100  2.5
 750 is in the top 1%.
  2.5  0.99
Example 3
• A manufacturer of potato chips claims that the average contents of
bags sold weighs 12 ounces. The distribution is known to be
normal with standard deviation =0.4 ounces. A random sample of
16 bags produced a sample mean weight of 11.84 ounces. Is it
reasonable to say that the average is 12?
Linear Combinations of Random Variables
• Suppose X and Y are independent r.v.’s with means
mx and my and variances x2 and y2 (a, b,c,and d are
scalars), then
 W=(aX+b) +( cY +d)
 V(W) = a2 x2+ c2 y2
 E(W) = amx +b+ cmy+d
 If X and Y are Normal then W is Normal.
Example (Sample Mean)
•
The individuals are Normally distributed, so
X 
n
x
i 1
i
/n
is Normally distributed.
With expected value m.
With variance /n
Example (Sample Mean)
•
The individuals are Normally distributed, so
X m
z
/ n
has the standard Normal distribution.
95%
-1.96
1.96
If we keep taking samples of 16 and calculating the sample mean:
• 95% of the time the interval will contain the true value:

 

.95  P  X  1.96
 m  X  1.96

n
n


• “The probability is .95 that the random interval
will include m.”

 
 X  1.96

n

Confidence Interval Estimation
• A 100(1-a)% confidence interval (CI) for an unknown
parameter q is a random interval [L,U] computed from
sample data that will contain the true q with probability
1-a. This probability is called the confidence level.
PL  q  U   1  a
Two-Sided Confidence Interval for the population mean
• The 100(1-a)% two-sided CI’s on m is given by
X  za / 2

n
 m  X  za / 2

n
The confidence interval gives us possible
values for the population mean.
•
Use 95% confidence
.4
.4
11.84  1.96
 m  11.84  1.96
16
16
11.64  m  12.04
• So it is reasonable to think that the mean is 12, but it could be as
low as 11.64.
What if we have to estimate the standard
deviation? (i.e. s=0.4)
The confidence interval needs to be bigger to account
for the fact that we don’t really know the variance.
X  za / 2

n
 m  X  za / 2

n

s
s 
.95  P  X  t0.025,n1
 m  X  t0.025, n1

n
n

z distribution
t distribution
-t0.025,n-1 -1.96
95%
95%
1.96 t0.025,n-1
Properties of t-distribution
• Let tv denote the density function curve for v degrees
of freedom
 Each tv curve is bell-shaped and centered at 0.
 Each tv curve is more spread out than the
standard normal (z) curve.
 As v increases, the spread of the corresponding tv
curve decreases.
 As v goes to infinity, the tv distribution approaches
the standard normal distribution.
t critical value
• ta,v: the number on the measurement axis for which
the area under the t curve with v degrees of freedom
to the right of ta,v is a.
CI’s on population mean
(variance estimated by n-1 degrees of freedom)
(Two-Sided CI): X  ta / 2,n 1
s
n
 m  X  ta / 2,n 1
s
n
• Use 95% confidence, a=0.05, n=16
t0.025,n 1  2.131
11.84  2.131
.4
 m  11.84  2.131
16
11.63  m  12.05
.4
16
• So it is reasonable to think that the mean is 12, but
it could be as low as 11.63.
Interpreting Confidence Intervals
There is a big difference between
Statistically Significant and
Practically Important.
Always look at both sides of the confidence interval and
think about how the value would affect your decision.
• Average time saved by driving by the “Shortcut” (-.5,1)
minutes.
• Average amount of money saved by buying from
Amazon.com (5,7) dollars.
• Average weight of gold in a pound of Lake Michigan
Sand (0,5) grams.
• Average error on yard markers on a football field (.02,
.04) inches.
Calculating and interpreting a confidence interval for a
difference between 2 design alternatives.
Could each of you rate a couple of designs that we have
sketched to fulfill your need? Rate these two designs on a
scale from 1-10, where 10 means it throws the ball, straight
and as far as possible using the specified rubber band.
Raw Data and Plot of Data
Person Slingshot Catapult
1
5
6
2
4
7
3
6
7
4
8
9
5
7
8
6
9
9
7
4
5
8
7
6
9
7
8
10
5
6
Ave
6.200
7.100
Stdev
1.687
1.370
Diff
1
System Design
103
91
81
7
1
6
0
5
1
4
-1
3
21
11
0
0.900
0.994
Slingshot
Catapult
Data and Better Plot – Look at Differences
(Difference = Catapult – Slingshot)
Person Slingshot Catapult
1
5
6
2
4
7
3
6
7
4
8
9
5
7
8
6
9
9
7
4
5
8
7
6
9
7
8
10
5
6
Ave
6.200
7.100
Stdev
1.687
1.370
Diff
1
3
1
1
1
0
1
-1
1
1
0.900
0.994
Comparison Plot
Slingshot
Catapult
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
Person
7
8
9
10
A Histogram of the Differences
Diff
1
3
1
1
1
0
1
-1
1
1
0.900
0.994
Mean = 0.900
StDev = 0.994
Histogram of Difference
-2
0
-1
1
8
7
0
1
6
Number of Responses
Person Slingshot Catapult
1
5
6
2
4
7
3
6
7
4
8
9
5
7
8
6
9
9
7
4
5
8
7
6
9
7
8
10
5
6
Ave
6.200
7.100
Stdev
1.687
1.370
1
7
5
2
0
4
3
1
3
4
0
2
5
0
1
0
-2
-1
0
1
2
Rating Difference
3
4
5
“Is the average difference between the two
design ratings significantly different than zero?”
Our estimate of the average difference
between the two ratings is 0.9 ± ??
We will create a confidence interval that,
with 95% confidence, contains the true
average difference in the ratings if we were
to ask all people in the target audience.
95% Confidence Interval
 Estimated Standard Deviation 
Estimated Average  tn -1 

n


 0.994 
95% CI:
0.900  2.262 

 10 
Estimated Average  0.900
Estimated
Standard Deviation  0.994
n  10 observations
 0.19, 1.61
Show Spreadsheet
95% Confidence Interval, (0.19, 1.61)
Statistical Significance: Is zero outside of the CI?
Yes, zero is outside the CI so we are 95% confident that the
catapult has a higher average rating than the slingshot because
all the numbers in the confidence interval are positive.
Practical Importance: Does either end of the CI have
a difference that really matters to the application?
On average, the Catapult could be as much as 1.61 rating
points better than the Slingshot, but it may be as little as
0.19 points better. Would the difference matter to you if
it was 0.19? No. 1.61? Yes.
Statistically Significant -vs- Practically Important
Assume a difference of 1.0 is important.
Stat.Sign
Pract.Imp.
No
(CI includes 0)
Yes
(0 is outside CI)
No, to both
ends.
Even if there is a
difference, it doesn’t
matter. (-0.2, 0.2)
There is a
difference, but it
doesn’t matter.
(0.1, 0.2)
Yes, to one
end of the CI.
We need more data,
to find out if there
really is any
difference. (-0.2,
1.5)
There is a
difference, we
might want more
data to be sure it
matters. (0.2, 1.5)
Yes, to both
ends.
We need a lot more
data. (-2.0, 2.0)
There is a clear
difference that
matters. (1.0, 1.5)
Show Spreadsheet with Estimate of Number
needed
Normal Assumption
• If we assume that each xi is normally distributed, then
the sample mean is a linear combination of Normally
distributed random variables and thus it has a Normal
distribution.
• If this is a good assumption, we have a complete
description of the sampling distribution for the sample
mean. N(m,2/n)
• What if that is a bad assumption?
Central Limit Theorem (C.L.T.)
• If X1, X2, …, Xn is a random sample of size n taken from
population with mean m and variance 2, and if X is the
sample mean, then the limiting form of the distribution of
X m
z
/ n
as n  
is the standard normal distribution.
“For sufficiently large n, the sample mean has an
approximately normal distribution, the larger the
sample, the better the approximation.”
50 Random Draws from a Uniform (0-10)
Frequency
10
Uniform (0-10)
5
0
0
2
4
6
C51
8
10
100 Means of 50 Random samples from a Uniform (0-10)
Frequency
20
Mean of 50
random sample
from (0-10)
10
0
4 .0 0 4 .2 5 4 .5 0 4 .7 5 5 .0 0 5 .2 5 5 .5 0 5 .7 5 6 .0 0
C52
Summary
If n is large
OR
The individuals are Normally distributed then
 2 

X ~ N  m ,
n 

and
X m
z
/ n
is the standard Normal distribution.
When n is large
• The assumptions that the sample is drawn from a normal
population and the variance is known can be relaxed.
 CLT allows us to regard the distribution of the sample
mean as N(m,2/n).
 The sample variance s2 can be regarded as an
accurate estimator of 2.
Hypothesis testing
• Statistical hypothesis: Statements about the parameters of
1 or more populations.
• Null hypothesis: ( H0)
 Statement being tested
 usually, “no effect” or “no difference”
• Alternative hypothesis: (HA or H1)
 statement you hope or expect to be true
 can be one sided
 if no specific idea, use two sided.
Null and Alternate Hypotheses
• Hypothesis: a statement of a theory or a claim.
• Recall that we want to assess the validity of a claim
against a counterclaim using sample data.
• The two competing claims must be mutually exclusive
and collectively exhaustive:
 Null Hypothesis (H0): the standard or favored claim.
 Alternate Hypothesis (HA): the claim to be proved.
• Begin with the assumption that H0 is true.
• If the data fail to contradict H0, then H0 is not rejected.
• The proof of HA is by contradiction of H0.
 Failing to reject H0 means that H0 cannot be ruled
out as a possible explanation for the observed
data (i.e., failing to reject H0 does not mean that
we accept it as true).
 Only when the data STRONGLY contradict H0, it is
rejected and HA is accepted.
Examples
• Is the average tube diameter being produced different from
the standard 3mm?
• Does adding compound X increase the average yield of the
process?
• Is the average SAT scores of UC students the same as NU
students?
Note
• Hypotheses are about parameters of the population,
not about the sample.
• H0 is always stated as equality.
• We either reject or do not reject the null hypothesis. The
rejection of the null hypothesis implies the acceptance of
the alternative hypothesis.
General steps for Hypothesis testing
• From the problem context, identify the parameter of
interest.
• State the null hypothesis, H0 involving an equality for
the parameter of interest.
• Specify an appropriate alternative hypothesis, H1.
• Choose a significance level a.
• Compute a 100(1-a)% confidence interval for the
parameter of interest.
• H0 should be rejected based on whether the
confidence interval contains the hypothesized value in
H0. (This is statistical significance)
• (Decisions should be made based on the practical
importance not just the statistical significance.)
Hypothesis testing on the mean - 2 known
Aircrew escape systems are powered by a
solid propellant. Specifications require that the
mean burning rate must be 50 cm/s. We know
the standard deviation of burning rate is  =
2.0 cm/s. The experimenter decides to specify
the significance level at a = 0.05. He selects a
random sample of n = 7 and obtains a sample
average burning rate 51.3 cm/s. What
conclusion should be drawn?
Testing Statistical Hypotheses
with confidence intervals
H0: m = 50 cm/s
A 100(1-a)% confidence interval
H1: m  50 cm/s
( X  Za / 2 / n , X  Za / 2 / n )
Za / 2 / n  1.96  2.0  / 7  1.5
( X  1.5)
( X  1.5)
X
Testing Statistical Hypotheses
with confidence intervals
H0: m = 50 cm/s
H1: m  50 cm/s
A 100(1-a)% confidence interval
( X  Za / 2 / n , X  Za / 2 / n )
X  51.3
(49.8, 52.78)
Acceptance Region
Critical
values
critical
region
X
Fail to reject H0
Usual Method of Hypothesis testing - two sided
To test:
H0 : m = m0
H1: m  m0
Rejection Acceptance
Region
Region
Rejection
Region
N (0,1)
a /2
 za / 2
a /2
0
za / 2
X  m0
Compute: Z 0 
which has a N(0,1) if H0 is true.
/ n
 za / 2  Z 0  za / 2
Fail to reject H0 if
X  m0 51.3  50
Z0 

 1.72  1.96
 / n 2.0 / 7
Fail to reject H0
Same as m0  za / 2 / n  X  m0  za / 2 / n
Type I error
Type I error - reject H0 when it is actually true.
Accept H0
Reject H0
Reject H0
m0
a = P(Type I error) = P(reject H0 when it is true)
- a: significant level of the test.
- 1 - a : confidence level of the test
Type II error
Type II error - fail to reject H0 when it is false.
b = P(Type II error)
= P( fail to reject H0 when it is false)
We need to have a particular alternative to find b.
Distribution of x if m A  52
Normal Distribution
Type II error
b = P(Type II error if m=52 and n=7)
= P( fail to reject H0 when it is false)
 P(48.5  X  51.5 given m  52 and   2.0
7)
How many standard deviations? Note that standard deviation of x is  /
48.5
51.5
m A  52
n
Type II error
b = P(Type II error if m=52 and n=7)
= P( fail to reject H0 when it is false)
 P( X  51.5 given m  52)
P(Type II error if m A is 52)
 upper rejection region boundary-m A 
 lower rejection region boundary-m A 
 






/
n

/
n




 51.5  52 
 48.5  52 
 





2.0
/
7
2.0
/
7




   0.6614     4.630 
 0.2549  0
 25%
Power of a test
• Power of a test
 Probability of correctly rejecting a false null
hypotheses
 A measure of the sensitivity of the test
• Power of a test = 1 - P(Type II error) = 1 - b
P(Type II error if m is 52)  0.25
Power of the test if m A is 52)  1- 0.25  0.75
• In general, if you decrease a, Type I error, then b, Type
II error will increase unless you increase sample size.
p- value
• p - value
 The probability that the test statistic will take on a
value as extreme as the observed value when H0
is true.
 The smallest level of significance, a, that would
lead to rejection of the H0.
 If p-value < a, reject H0.
 If p-value > a, do not reject H0.
Understanding p-values
with confidence intervals
H0: m = 50 cm/s
H1: m  50 cm/s
A 100(1-p)% confidence interval
( X  Z p / 2 / n , X  Z p / 2 / n )
X  51.3
(50.000001, 52.6)
A 100(1-a)% confidence interval
( X  Za / 2 / n , X  Za / 2 / n )
X  51.3
(49.8, 52.78)
X
Understanding p-values
with confidence intervals
A 100(1-p)% confidence interval
( X  Z p / 2 / n , X  Z p / 2 / n )
X  51.3
(50.0001, 52.6)
X  Z p / 2 / n  50
(50  X ) n (51.3  50) 7

 1.72

2.0
p / 2  .0427
p  .0854  a  .05
Do not reject H 0
Z p/2 