* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Essentials of Biostatistics in Public Health
Survey
Document related concepts
Transcript
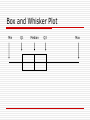
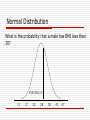
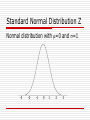
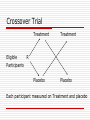
CPH Exam Review Biostatistics Lisa Sullivan, PhD Associate Dean for Education Professor and Chair, Department of Biostatistics Boston University School of Public Health Outline and Goals Overview of Biostatistics (Core Area) Terminology and Definitions Practice Questions An archived version of this review, along with the PPT file, will be available on the NBPHE website (www.nbphe.org) under Study Resources Biostatistics Two Areas of Applied Biostatistics: Descriptive Statistics Summarize a sample selected from a population Inferential Statistics Make inferences about population parameters based on sample statistics. Variable Types Dichotomous variables have 2 possible responses (e.g., Yes/No) Ordinal and categorical variables have more than two responses and responses are ordered and unordered, respectively Continuous (or measurement) variables assume in theory any values between a theoretical minimum and maximum We want to study whether individuals over 45 years are at greater risk of diabetes than those younger than 45. What kind of variable is age? 1. 2. 3. 4. Dichotomous Ordinal Categorical Continuous We are interested in assessing disparities in infant morbidity by race/ethnicity. What kind of variable is race/ethnicity? 1. 2. 3. 4. Dichotomous Ordinal Categorical Continuous Numerical Summaries of Dichotomous, Categorical and Ordinal Variables Frequency Distribution Table Heath Status Freq. Rel. Freq. Cumulative Freq Cumulative Rel. Freq. Excellent 19 38% 19 38% Very Good 12 24% 31 62% Good 9 18% 40 80% Fair 6 12% 46 92% Poor 4 8% 50 100% n=50 100% Ordinal variables only N pa ra t ed ar ri ed ev er Marital Status ed ar ri ed id ow M W D iv or ce d Se M Frequency Frequency Bar Chart 30 25 20 15 10 5 0 % Relative Frequency Histogram 40 35 30 25 20 15 10 5 0 Poor Fair Good Very Good Health Status Excellent Continuous Variables Assume, in theory, any value between a theoretical minimum and maximum Quantitative, measurement variables Example – systolic blood pressure Standard Summary: n = 75, X = 123.6, s = 19.4 Second sample n = 75, X = 128.1, s = 6.4 Summarizing Location and Variability When there are no outliers, the sample mean and standard deviation summarize location and variability When there are outliers, the median and interquartile range (IQR) summarize location and variability, where IQR = Q3-Q1 Outliers <Q1–1.5 IQR or >Q3+1.5 IQR Mean Vs. Median Box and Whisker Plot Min Q1 Median Q3 Max Comparing Samples with Box and Whisker Plots 2 1 100 110 120 130 140 Systolic Blood Pressure 150 160 What type of display is shown below? Percent Patients by Disease Stage 35 30 % 25 20 15 10 5 0 I 1. 2. 3. 4. II III IV Frequency bar chart Relative frequency bar chart Frequency histogram Relative frequency histogram The distribution of SBP in men, 20-29 years is shown below. What is the best summary of a typical value 1. 2. 3. 4. Mean Median Interquartile range Standard Deviation When data are skewed, the mean is higher than the median. 1. True 2. False The best summary of variability for the following continuous variable is 1. 2. 3. 4. Mean Median Interquartile range Standard Deviation Numerical and Graphical Summaries Dichotomous and categorical Frequencies and relative frequencies Bar charts (freq. or relative freq.) Ordinal Frequencies, relative frequencies, cumulative frequencies and cumulative relative frequencies Histograms (freq. or relative freq. Continuous n, X and s or median and IQR (if outliers) Box whisker plot What is the probability of selecting a male with optimal blood pressure? Blood Pressure Category Optimal Normal Pre-Htn Htn Male Female Total Total 20 15 15 30 80 5 15 25 25 70 25 30 40 55 150 1. 20/25 2. 20/80 3. 20/150 What is the probability of selecting a patient with Pre-Htn or Htn? Blood Pressure Category Optimal Normal Pre-Htn Htn Male Female Total Total 20 15 15 30 80 5 15 25 25 70 25 30 40 55 150 1. 95/150 2. 45/80 3. 55/150 What proportion of men have prevalent CVD? CVD Free of CVD Men 35 265 Women 45 355 1. 35/80 2. 35/265 3. 35/300 What proportion of patients with CVD are men ? CVD Free of CVD Men 35 265 Women 45 355 1. 35/700 2. 35/80 3. 80/300 Are Family History and Current Status Independent? Example. Consider the following table which cross classifies subjects by their family history of CVD and current (prevalent) CVD status. Current CVD Family History No Yes No 215 25 Yes 90 15 P(Current CVD| Family Hx) = 15/105 = 0.143 P(Current CVD| No Family Hx) = 25/240 = 0.104 Are symptoms independent of disease? Disease No Disease Total Symptoms 25 225 250 No Symptoms 50 450 500 1. No 2. Yes Probability Models – Binomial Distribution Two possible outcomes: success and failure Replications of process are independent P(success) is constant for each replication n! P(x) p x (1 p) n x x!(n x)! Mean=np, variance=np(1-p) Probability Models – Poisson Distribution Two possible outcomes: success and failure Replications of process are independent Often used to model counts (often used to model rare events) P(x) (e μ ) / x! -μ x Mean=m, variance=m Probability Models – Normal Distribution Model for continuous outcome Mean=median=mode Normal Distribution Properties of Normal Distribution I) The normal distribution is symmetric about the mean (i.e., P(X > m) = P(X < m) = 0.5). ii) The mean and variance (m and s2) completely characterize the normal distribution. iii) The mean = the median = the mode iv) Approximately 68% of obs between mean + 1 sd 95% between mean + 2 sd, and >99% between mean + 3 sd Normal Distribution Body mass index (BMI) for men age 60 is normally distributed with a mean of 29 and standard deviation of 6. What is the probability that a male has BMI < 29? P(X<29)= 0.5 11 17 23 29 35 41 47 Normal Distribution What is the probability that a male has BMI less than 30? P(X<30)=? 11 17 23 29 35 41 47 Standard Normal Distribution Z Normal distribution with m=0 and s=1 -3 -2 -1 0 1 2 3 Normal Distribution x μ 30 29 Z 0.17 σ 6 P(X<30)= P(Z<0.17) = 0.5675 From a table of standard normal probabilities or statistical computing package. Comparing Systolic Blood Pressure (SBP) Comparing systolic blood pressure (SBP) Suppose for Males Age 50, SBP is approximately normally distributed with a mean of 108 and a standard deviation of 14 Suppose for Females Age 50, SBP is approximately normally distributed with a mean of 100 and a standard deviation of 8 If a Male Age 50 has a SBP = 140 and a Female Age 50 has a SBP = 120, who has the “relatively” higher SBP ? Normal Distribution ZM = (140 - 108) / 14 = 2.29 ZF = (120 - 100) / 8 = 2.50 Which is more extreme? Percentiles of the Normal Distribution The kth percentile is defined as the score that holds k percent of the scores below it. Eg., 90th percentile is the score that holds 90% of the scores below it. Q1 = 25th percentile, median = 50th percentile, Q3 = 75th percentile Percentiles For the normal distribution, the following is used to compute percentiles: X=m+Zs where m = mean of the random variable X, s = standard deviation, and Z = value from the standard normal distribution for the desired percentile (e.g., 95th, Z=1.645). 95th percentile of BMI for Men: 29+1.645(6) = 38.9 Central Limit Theorem (Non-normal) population with m, s Take samples of size n – as long as n is sufficiently large (usually n > 30 suffices) The distribution of the sample mean is approximately normal, therefore can use Z to compute probabilities x μ Z σ n Standard error Statistical Inference There are two broad areas of statistical inference, estimation and hypothesis testing. Estimation. Population parameter is unknown, sample statistics are used to generate estimates. Hypothesis Testing. A statement is made about parameter, sample statistics support or refute statement. What Analysis To Do When Nature of primary outcome variable Continuous, dichotomous, categorical, time to event Number of comparison groups One, 2 independent, 2 matched or paired, > 2 Associations between variables Regression analysis Estimation Process of determining likely values for unknown population parameter Point estimate is best single-valued estimate for parameter Confidence interval is range of values for parameter: point estimate + margin of error point estimate + t SE (point estimate) Hypothesis Testing Procedures 1. Set up null and research hypotheses, select a 2. Select test statistic 3. Set up decision rule 4. Compute test statistic 5. Draw conclusion & summarize significance (p-value) P-values P-values represent the exact significance of the data Estimate p-values when rejecting H0 to summarize significance of the data (approximate with statistical tables, exact value with computing package) If p < a then reject H0 Errors in Hypothesis Tests Conclusion of Statistical Test Do Not Reject H0 Reject H0 H0 true Correct Type I error H0 false Type II error Correct Continuous Outcome Confidence Interval for m Continuous outcome - 1 Sample n > 30 n < 30 s XZ Xt n s n Example. 95% CI for mean waiting time at ED Data: n=100, X=37.85 and s=9.5 mins 37.85 1.96 9.5 100 37.85 + 1.86 (35.99 to 39.71) Statistical computing packages use t throughout. New Scenario Outcome is dichotomous Result of surgery (success, failure) Cancer remission (yes/no) One study sample Data On each participant, measure outcome (yes/no) x n, x=# positive responses, p̂ n Dichotomous Outcome Confidence Interval for p Dichotomous outcome - 1 Sample p̂(1 - p̂) p̂ Z n min[np̂, n(1 p̂)] 5 otherwise, exact procedures Example. In the Framingham Offspring Study (n=3532), 1219 patients were on antihypertensive medications. Generate 95% CI. 0.345 1.96 0.345(1 - 0.345) 3532 0.345 + 0.016 (0.329, 0.361) One Sample Procedures – Comparisons with Historical/External Control Continuous H0: mm0 H1: m>m0, <m0, ≠m0 n>30 n<30 Z t X - μ0 s/ n Dichotomous H0: pp0 H1: p>p0, <p0, ≠p0 Z p̂ - p 0 p 0 (1 - p 0 ) n X - μ0 min[np0 , n(1 p 0 )] 5 s/ n otherwise, exact procedures One Sample Procedures – Comparisons with Historical/External Control Categorical or Ordinal outcome c2 Goodness of fit test H0: p1p10, p2p20, . . . , pkpk0 H1: H0 is false (O - E ) χ =Σ E 2 2 New Scenario Outcome is continuous SBP, Weight, cholesterol Two independent study samples Data On each participant, identify group and measure outcome 2 2 n1 , X1 , s1 (or s1 ), n 2 , X 2 , s 2 (or s 2 ) Two Independent Samples Cohort Study - Set of Subjects Who Meet Study Inclusion Criteria Group 1 Mean Group 1 Group 2 Mean Group 2 Two Independent Samples RCT: Set of Subjects Who Meet Study Eligibility Criteria Randomize Treatment 1 Mean Trt 1 Treatment 2 Mean Trt 2 Continuous Outcome Confidence Interval for (m1m2) Continuous outcome - 2 Independent Samples n1>30 and n2>30 n1<30 or n2<30 Sp 1 1 (X1 - X 2 ) ZSp n1 n 2 1 1 (X1 - X 2 ) tSp n1 n 2 (n 1 1)s 12 (n 2 1)s 22 n1 n 2 2 Hypothesis Testing for (m1m2) Continuous outcome 2 Independent Sample H0: m1m2 (m1m2 = 0) H1: m1>m2, m1<m2, m1≠m2 Hypothesis Testing for (m1m2) Test Statistic n1>30 and n2> 30 n1<30 or n2<30 Z X1 - X 2 1 1 Sp n1 n 2 t X1 - X 2 1 1 Sp n1 n 2 An RCT is planned to show the efficacy of a new drug vs. placebo to lower total cholesterol. What are the hypotheses? 1. H0: mP=mN H1: mP>mN 2. H0: mP=mN H1: mP<mN 3. H0: mP=mN H1: mP≠mN New Scenario Outcome is dichotomous Result of surgery (success, failure) Cancer remission (yes/no) Two independent study samples Data On each participant, identify group and measure outcome (yes/no) n1 , p̂1 , n 2 , p̂ 2 Dichotomous Outcome Confidence Interval for (p1p2) Dichotomous outcome - 2 Independent Samples min[n 1p̂1 , n1 (1 p̂1 ), n 2p̂2 , n 2 (1 p̂2 )] 5 p̂1 (1 - p̂1 ) p̂ 2 (1 p̂ 2 ) (p̂1 - p̂ 2 ) Z n1 n2 Measures of Effect for Dichotomous Outcomes Outcome = dichotomous (Y/N or 0/1) Risk=proportion of successes = x/n Odds=ratio of successes to failures=x/(n-x) Measures of Effect for Dichotomous Outcomes Risk Difference = p̂1 - p̂ 2 Relative Risk = p̂1/p̂ 2 p̂1 /(1 p̂1 ) Odds Ratio = p̂ 2 /(1 p̂ 2 ) Confidence Intervals for Relative Risk (RR) Dichotomous outcome 2 Independent Samples (n1 - x1 )/x 1 (n 2 - x 2 )/x 2 ln( R̂R) Z n1 n2 exp(lower limit), exp(upper limit) Confidence Intervals for Odds Ratio (OR) Dichotomous outcome 2 Independent Samples 1 1 1 1 ln( ÔR) Z x1 (n1 x1 ) x 2 (n 2 x 2 ) exp(lower limit), exp(upper limit) Hypothesis Testing for (p1-p2) Dichotomous outcome 2 Independent Sample H0: p1=p2 H1: p1>p2, p1<p2, p1≠p2 Test Statistic min[n 1p̂1 , n1 (1 p̂1 ), n 2p̂2 , n 2 (1 p̂2 )] 5 Z p̂1 - p̂ 2 1 1 p̂(1 - p̂) n1 n 2 Two (Independent) Group Comparisons Difference in birth weight is -106 g, 95% CI for difference in mean Birth weight: (-175.3 to -36.7) New Scenario Outcome is continuous SBP, Weight, cholesterol Two matched study samples Data On each participant, measure outcome under each experimental condition Compute differences (D=X1-X2) n, X d , s d Two Dependent/Matched Samples Subject ID 1 2 . . Measure 1 55 42 Measure 2 70 60 Measures taken serially in time or under different experimental conditions Crossover Trial Treatment Treatment Placebo Placebo Eligible R Participants Each participant measured on Treatment and placebo Confidence Intervals for md Continuous outcome 2 Matched/Paired Samples n > 30 sd Xd Z n n < 30 sd Xd t n Hypothesis Testing for md Continuous outcome 2 Matched/Paired Samples H0: md0 H1: md>0, md<0, md≠0 Test Statistic n>30 n<30 Z t Xd - μ d sd n Xd - μd sd n Independent Vs Matched Design Statistical Significance versus Effect Size P-value summarizes significance Confidence intervals give magnitude of effect (If null value is included in CI, then no statistical significance) The null value of a difference in means is… 1. 2. 3. 4. 0 0.5 1 2 The null value of a mean difference is… 1. 2. 3. 4. 0 0.5 1 2 The null value of a relative risk is… 1. 2. 3. 4. 0 0.5 1 2 The null value of a difference in proportions is… 1. 2. 3. 4. 0 0.5 1 2 The null value of an odds ratio is… 1. 2. 3. 4. 0 0.5 1 2 A two sided test for the equality of means produces p=0.20. Reject H0? 1. Yes 2. No 3. Maybe Hypothesis Testing for More than 2 Means - Analysis of Variance Continuous outcome k Independent Samples, k > 2 H0: m1m2m3 … mk H1: Means are not all equal Test Statistic F Σn j (X j X) 2 /(k 1) ΣΣ(X X j ) 2 /(N k) F is ratio of between group variation to within group variation (error) ANOVA Table Source of Variation Sums of Squares df Between 2 SSB = Σ n j (X j - X ) Treatments k-1 2 Error SSE = Σ Σ (X - X j) Total SST = Σ Σ (X - X ) 2 N-k N-1 Mean Squares F SSB/k-1 MSB/MSE SSE/N-k ANOVA When the sample sizes are equal, the design is said to be balanced Balanced designs give greatest power and are more robust to violations of the normality assumption Extensions Multiple Comparison Procedures – Used to test for specific differences in means after rejecting equality of all means (e.g., Tukey, Scheffe) Higher-Order ANOVA - Tests for differences in means as a function of several factors Extensions Repeated Measures ANOVA - Tests for differences in means when there are multiple measurements in the same participants (e.g., measures taken serially in time) c2 Test of Independence Dichotomous, ordinal or categorical outcome 2 or More Samples H0: The distribution of the outcome is independent of the groups H1: H0 is false Test Statistic 2 (O E) χ2 E c2 Test of Independence Data organization (r by c table) Outcome Group 1 2 3 A 20% 40% 40% B 50% 25% 25% C 90% 5% 5% Is there distribution of the outcome different (associated with) groups What Tests Were Used? In Framingham Heart Study, we want to assess risk factors for Impaired Glucose Outcome = Glucose Category Diabetes (glucose > 126), Impaired Fasting Glucose (glucose 100-125), Normal Glucose Risk Factors Sex Age BMI (normal weight, overweight, obese) Genetics What test would be used to assess whether sex is associated with Glucose Category? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether age is associated with Glucose Category? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether BMI is associated with Glucose Category? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other In Framingham Heart Study, we want to assess risk factors for Glucose Level Consider a Secondary Outcome = Fasting Glucose Level Risk Factors Sex Age BMI (normal weight, overweight, obese) Genetics What test would be used to assess whether sex is associated with Glucose Level? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether BMI is associated with Glucose Level? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether age is associated with Glucose Level? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other In Framingham Heart Study, we want to assess risk factors for Diabetes Consider a Tertiary Outcome = Diabetes Vs No Diabetes Risk Factors Sex Age BMI (normal weight, overweight, obese) Genetics What test would be used to assess whether sex is associated with Diabetes? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether BMI is associated with Diabetes? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other What test would be used to assess whether age is associated with Diabetes? 1. 2. 3. 4. 5. ANOVA Chi-Square GOF Chi-Square test of independence Test for equality of means Other Correlation Correlation (r)– measures the nature and strength of linear association between two variables at a time Regression – equation that best describes relationship between variables What is the most likely value of r for the data shown below? Y * * * * * * * * * * * * * * * * * * * * * * * * X 1. 2. 3. 4. r=-0.5 r=0 r=0.5 r=1 What is the most likely value of r for the data shown below? Y * * * * * * * * * 1. 2. 3. 4. r=-0.5 r=0 r=0.5 r=1 * * * * * * * * X Simple Linear Regression Y = Dependent, Outcome variable X = Independent, Predictor variable ŷ = b0 + b1 x b0 is the Y-intercept, b1 is the slope Simple Linear Regression Assumptions Linear relationship between X and Y Independence of errors Homoscedasticity (constant variance) of the errors Normality of errors Multiple Linear Regression Useful when we want to jointly examine the effect of several X variables on the outcome Y variable. Y = continuous outcome variable X1, X2, …, Xp = set of independent or predictor variables ŷ. = b0 + b1 x1 + b2 x2 + . . . + bp xp Multiple Regression Analysis Model is conditional, parameter estimates are conditioned on other variables in model Perform overall test of regression If significant, examine individual predictors Relative importance of predictors by pvalues (or standardized coefficients) Multiple Regression Analysis Predictors can be continuous, indicator variables (0/1) or a set of dummy variables Dummy variables (for categorical predictors) Race: white, black, Hispanic Black (1 if black, 0 otherwise) Hispanic (1 if Hispanic, 0 otherwise) Definitions Confounding – the distortion of the effect of a risk factor on an outcome Effect Modification – a different relationship between the risk factor and an outcome depending on the level of another variable Multiple Regression for SBP: Comparison of Parameter Estimates Age Male BMI BP Meds Simple b 1.03 -2.26 1.80 33.38 Models p <.0001 .0009 <.0001 <.0001 Multiple b 0.86 -2.22 1.48 24.12 Regression p <.0001 .0002 <.0001 <.0001 Focus on the association between BP meds and SBP… RCT of New Drug to Raise HDL Example of Effect Modification Women N Mean Std Dev New drug 40 38.88 3.97 Placebo 41 39.24 4.21 Men N Mean Std Dev New drug 10 45.25 1.89 Placebo 9 39.06 2.22 Simple Logistic Regression Outcome is dichotomous (binary) We model the probability p of having the disease. b 0 b1X e p̂ b 0 b1X 1 e p̂ b 0 b1x logit( p̂) ln 1 p̂ Multiple Logistic Regression Outcome is dichotomous (1=event, 0=non-event) and p=P(event) Outcome is modeled as log odds p̂ b 0 b1x1 b 2 x 2 ... b p x p ln 1 - p̂ Multiple Logistic Regression for Birth Defect (Y/N) Predictor Intercept Smoke Age b p OR (95% CI for OR) -1.099 0.0994 1.062 0.2973 2.89 (0.34, 22.51) 0.298 0.0420 1.35 (1.02, 1.78) Interpretation of OR for age: The odds of having a birth defect for the older of two mothers differing in age by one year is estimated to be 1.35 times higher after adjusting for smoking. Survival Analysis Outcome is the time to an event. An event could be time to heart attack, cancer remission or death. Measure whether person has event or not (Yes/No) and if so, their time to event. Determine factors associated with longer survival. Survival Analysis Incomplete follow-up information Censoring Measure follow-up time and not time to event We know survival time > follow-up time Log rank test to compare survival in two or more independent groups Survival Curve – Survival Function Comparing Survival Curves H0: Two survival curves are equal c2 Test with df=1. Reject H0 if c2 > 3.84 c2 = 6.151. Reject H0. Cox Proportional Hazards Model Model: ln(h(t)/h0(t)) = b1X1 + b2X2 + … + bpXp Exp(bi) = hazard ratio Model used to jointly assess effects of independent variables on outcome (time to an event). Outcome= all-cause mortality Age and Sex as predictors bi p Age 0.11149 0.0001 Male Sex 0.67958 0.0001 HR 1.118 1.973 Sample Size Determination Need sample to ensure precision in analysis Sample size determined based on type of planned analysis CI Test of hypothesis Determining Sample Size for Confidence Interval Estimates Goal is to estimate an unknown parameter using a confidence interval estimate Plan a study to sample individuals, collect appropriate data and generate CI estimate How many individuals should we sample? Determining Sample Size for Confidence Interval Estimates Confidence intervals: point estimate + margin of error Determine n to ensure small margin of error (precision) – accounting for attrition! Must specify desired margin of error, confidence level and variability of parameter Determining Sample Size for Hypothesis Testing How many participants are needed to ensure that there is a high probability of rejecting H0 when it is really false? Determine n to ensure high power (usually 80% or 90%) – accounting for attrition! Must specify desired power, a and effect size (difference in parameter under H0 versus H1) Determining Sample Size for Hypothesis Testing b and Power are related to the sample size, level of significance (a) and the effect size (difference in parameter of interest under H0 versus H1) Power is higher with larger a Power is higher with larger effect size Power is higher with larger sample size Sample Size Determination Critical Ethical Sometimes difficult