Download Advanced Data Structure

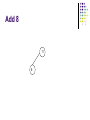
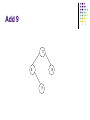
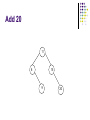
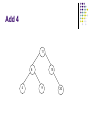
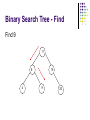
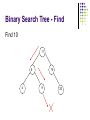
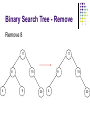
Advanced Data Structure
By Kayman
21 Jan 2006
Outline

Review of some data structures




Array
Linked List
Sorted Array
New stuff




3 of the most important data structures in OI (and your own
programming)
Binary Search Tree
Heap (Priority Queue)
Hash Table
Review


How to measure the merits of a data
structure?
Time complexity of common operations





Function Find(T : DataType) : Element
Function Find_Min() : Element
Procedure Add(T : DataType)
Procedure Remove(E : Element)
Procedure Remove_Min()
Review - Array






Here Element is simply the integer index of the array cell
Find(T)
 Must scan the whole array, O(N)
Find_Min()
 Also need to scan the whole array, O(N)
Add(T)
 Simply add it to the end of the array, O(1)
Remove(E)
 Deleting an element creates a hole
 Copy the last element to fill the hole, O(1)
Remove_Min()
 Need to Find_Min() then Remove(), O(N)
Review - Linked List


Element is a pointer to the object
Find(T)


Find_Min()


Just add it to a convenient position (e.g. head), O(1)
Remove(E)


Scan the whole list, O(N)
Add(T)


Scan the whole list, O(N)
With suitable implementation, O(1)
Remove_Min()

Need to Find_Min() then Remove(), O(N)
Review - Sorted Array






Like array, Element is the integer index of the cell
Find(T)
 We can use binary search, O(logN)
Find_Min()
 The first element must be the minimum, O(1)
Add(T)
 First we need to find the correct place, O(logN)
 Then we need to shift the array by 1 cell, O(N)
Remove(E)
 Deleting an element creates a hole
 Need to shift the of array by 1 cell, O(N)
Remove_Min()
 Can be O(1) or O(N) depending on choice of implementation
Review - Summary
Array
Find
O(N)
Find_Min
O(N)
Add
O(1)
Remove
O(1)
Remove_M O(N)
in

Linked List
O(N)
O(N)
O(1)
O(1)
O(N)
Sorted Array
O(logN)
O(1)
O(N)
O(N)
O(1) or O(N)
If we are going to perform a lot of these
operations (e.g. N=100000), none of these is
fast enough!
Advanced Data
Structure
Binary Search Tree
What is a Binary Search Tree?


Use a binary tree to store the data
Maintain this property

Left Subtree < Node < Right Subtree
11
8
4
15
9
20
Binary Search Tree - Add
11,8,15,9,20,4
11
8
4
15
9
20
Add 11
11
Add 8
11
8
Add 15
11
8
15
Add 9
11
8
15
9
Add 20
11
8
15
9
20
Add 4
11
8
4
15
9
20
Binary Search Tree - Find
Find 9
11
8
4
15
9
20
Binary Search Tree - Find
Find 10
11
8
4
15
9
20
Binary Search Tree - Remove

Case I : Removing a leaf node

Easy
Binary Search Tree - Remove
Remove 9
11
8
4
11
15
9
8
20
4
15
20
Binary Search Tree - Remove

Case I : Removing a leaf node


Easy
Case II : Removing a node with a single child

Replace the removed node with its child
Binary Search Tree - Remove
Remove 15
11
8
4
11
15
9
8
20
4
20
9
Binary Search Tree - Remove

Case I : Removing a leaf node


Case II : Removing a node with a single child


Easy
Replace the removed node with its child
Case III : Removing a node with 2 children



Replace the removed node with the minimum
element in the right subtree (or maximum element
in the left subtree)
This may create a hole again
Apply Case I or II
Binary Search Tree - Remove
Remove 8
11
8
4
11
15
9
9
20
4
15
20
Binary Search Tree - Remove




Case I : Removing a leaf node
 Easy
Case II : Removing a node with a single child
 Replace the removed node with its child
Case III : Removing a node with 2 children
 Replace the removed node with the minimum element in the right
subtree (or maximum element in the left subtree)
 This may create a hole again
 Apply Case I or II
Sometimes you can avoid this by using “Lazy Deletion”
 Mark a node as removed instead of actually removing it
 Less coding, performance hit not big if you are not doing this
frequently (may even save time)
Binary Search Tree - Remove
Remove 11
11
8
4
del
15
9
8
20
4
15
9
20
Binary Search Tree - Summary




Add() is similar to Find()
Find_Min()
 Just walk to the left, easy
Remove_Min()
 Equivalent to Find_Min() then Remove()
Summary
 Find() : O(logN)
 Find_Min() : O(logN)
 Remove_Min() : O(logN)
 Add() : O(logN)
 Remove() : O(logN)
 The BST is “supposed” to behave like that
Binary Search Tree - Problems



In reality…
 All these operations are O(logN) only if the tree is balanced
 Inserting a sorted sequence degenerates into a linked list
The real upper bounds
 Find() : O(N)
 Find_Min() : O(N)
 Remove_Min() : O(N)
 Add() : O(N)
 Remove() : O(N)
Solution
 AVL Tree, Red Black Tree
 Use “rotations” to maintain balance
 Both are difficult to implement, rarely used
Advanced Data
Structure
Heap (Priority Queue)
What is a Heap?


A (usually) complete binary tree
for Priority Queue
 Enqueue = Add
 Dequeue = Find_Min and
Remove_Min
Heap Property
 Every node’s value is greater
than those of its decendants
Heap - Implementation


Usually we use an
array to simulate a
heap
Assume nodes are
indexed 1, 2, 3, ...



Parent = [Node / 2]
Left Child = Node*2
Right Child =
Node*2 + 1
Heap - Add


Append the new element at the end
Shift it up until the heap property is restored
Heap - Remove_Min


Replace the root with the last element
Shift it down until the heap property is restored
Heap - Build_Heap

Apply shift down function to half nodes from
middle to top
Heap - Summary

Find() is usually not supported by a heap


Remove() is equivalent to applying Remove_Min()
on a subtree


You may scan the whole tree / array if you really want
Remember that any subtree of a heap is also a heap
Summary





Find() : O(N)
// We usually don’t use Heap for this
Find_Min() : O(1)
Remove_Min() : O(logN)
Add() : O(logN)
Remove() : O(logN)
Advanced Data
Structure
Hash Table
What is a Hash Table?




Question
 We have a Mark Six result (6 integers in the range 1..49)
 We want to check if our bet matches it
 What is the most efficient way?
Answer
 Use a boolean array with 49 cells
 Checking a number is O(1)
Problem
 What if the range of number is very large?
 What if we need to store strings?
Solution
 Use a “Hash Function” to compress the range of values
Hash Table




Suppose we need to store values
between 0 and 99, but only have an
array with 10 cells
We can map the values [0,99] to [0,9]
by taking modulo 10. The result is
the “Hash Value”
Adding, finding and removing an
element are O(1)
It is even possible to map the strings
to integers, e.g. “ATE” to
(1*26*26+20*26+5) mod 10
Hash Table - Collision

But this approach has an inherent problem


What happens if two data has the same hash
value?
Two major methods to deal with this


Chaining (Also called Open Hashing)
Open Addressing (Also called Closed Hashing)
Hash Table - Chaining


Keep a link list at each
hash table cell
On average, Add / Find
/ Remove is O(1+a)


a = Load Factor = # of
stored elements / # of
cells
If hash function is
“random” enough,
usually can get the
average case
Hash Table - Open Addressing



If you don’t want to implement a linked list…
An alternative is to skip a cell if it is occupied
The following diagram illustrates “Linear Probing”
Hash Table - Open Addressing


Find() must continue until a blank cell is reached
Remove() must use Lazy Deletion, otherwise further
operations may fail
Hash Table - Summary

Find_Min() and Remove_Min() are usually not supported in a
Hash Table
 You may scan the whole tree / array if you really want

For Chaining
 Find() : O(1+a)
 Add() : O(1+a)
 Remove() : O(1+a)
For Open Adressing
 Find() : O(1 / 1-a)
 Add() : O(1 / 1-a)
 Remove() : O(ln(1/1-a)/a + 1/a)


Both are close to O(1) if a is kept small (< 50%)
Additional Information

Judge problems





Past contest problems


1020 – Left Join
1021 – Inner Join
1019 – Addition II
1090 – Diligent
NOI2004 Day 1 – Cashier
Good place to find related information - Wikipedia



http://en.wikipedia.org/wiki/Binary_search_tree
http://en.wikipedia.org/wiki/Binary_heap
http://en.wikipedia.org/wiki/Hash_table