* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download hyperoctree
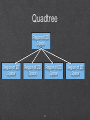
Survey
Document related concepts
Transcript
Quadtrees and Octrees Dr. Randy M. Kaplan Introduction Quadtrees Hierarchical Spacial Based on - Recursive decomposition of space 2 Quadtree Representation of 2-dimensional space Space is decomposed using separators Parallel to the coordinate axis Split a region into four(4) regions Southwest Northwest Southeast Northeast 3 Quadtree A node corresponds to the region The decomposition of the region into four(4) can be resprensented as a subtree whose parent is the original region one(1) child for each decomposed region 4 Quadtree Region of 2D Space Region of 2D Space Region of 2D Space Region of 2D Space 5 Region of 2D Space Octree 3D Analog to Quadtree Region is split into eight(8) sub-regions using planes parallel to the coordinate axis A region node will have 8 children 6 Octree 7 Octree 8 Octree 9 More Than 3 Dimensions In the case where more than 3 dimensions need to be represented the term for the data structure is HYPEROCTREE 10 Quadtree/Octree Allow space to be represented at various levels of granularity Allows quick focusing on regions of interest Example Find all points in a dataset that lie within a given distance from a query point 11 Quadtree/Octree Find all points in a dataset that lie within a given distance from a query point AKA Spherical Region Query 12 Spherical Region Query In the absence of any data structure all points in the dataset will need to be analyzed If a quadtree is available, large regions of points can be eliminated from the search 13 Quadtree Construction Start with a square, cubic, or hypercubic region (depending on dimensionality of the dataset) Decompose the initial region according to one of two strategies 14 Quadtree Construction Guide decomposition by input data Guide decomposition by principal of equal subdivision 15 Quadtree Construction Guide decomposition by input data Resulting tree size will be proportional to input If all data is available a priori it is possible to make the tree height balanced 16 Quadtree Construction Guide decomposition by input data Although the resulting tree has desirable properties, it also has some disadvantage, i.e., Difficult to make the data structure dynamic Deletion of data is difficult 17 Quadtree Construction Decomposition based on equal subdivision Distribution of spacial data determines the characteristics of the resulting tree 18 Quadtree Construction Decomposition based on equal subdivision Tree will be height balanced and size will be linear when the spatial data is distributed uniformly 19 Quadtree Construction Decomposition based on equal subdivision Height and size properties deteriorate as the distribution becomes non-uniform 20 Termination Criteria In the subdivision process, when is it time to stop subdividing? Two criteria can be used in an OR or AND configuration Resolution Requirement Condition on Region Requirement 21 Ubiquity The quadtree is a ubiquitous data structure much as the binary tree is also a ubiquitous data structure It can be found applied to many different areas of spatial computing 22 Ubiquity Computational Geometry Computer-aided design Computer graphics Databases Geographic Information Systems Image processing Pattern recognition 23 Quadtrees for Point Data Set of n points in d dimensional space Principle application Organize multidimensional data Facilitate queries requiring spatial information 24 Quadtrees for Point Data Kinds of queries Range query Spherical region query All nearest neighbors query 25 Range Query Given a range of values for each dimension, find all points that lie within the range Equivalent to finding all points lying within a hyper-rectangular region 26 Spherical Region Query Given, point p, radius r Find all the points that lie within a distance r from p 27 Nearest Neighbor Query Given n points, find the nearest neighbor of each point within the set 28 Point Quadtrees Point quadtree is a natural generalization of the binary search tree We will consider the 2-dimensional case Begin with a square region containing all of the input points 29 Point Quadtrees 30 Point Quadtrees How to Make a Quadtree Choose an arbitrary point 31 Point Quadtrees The point becomes the root of the tree 32 Point Quadtrees Use lines that are parallel to the coordinate axis Draw these lines to intersect with the chosen point to divide the region 33 Point Quadtrees Each of the subregions are recursively divided in a similar way In this way the point quadtree is produced 34 Point Quadtrees When a point is on a boundary it is necessary to adopt some conventions to specify to which region the point belongs Points lying on the left and bottom edges of a region are considered included in the region 35 Point Quadtrees Points lying on the left and bottom edges of a region are considered included in the region Points lying on the right and top edges of a region are considered not to be part of the region 36 Point Quadtrees When all of the points are known in advance, it is possible to construct a balanced tree 37 Point Quadtrees A simple way to accomplish this is to sort the points with one of the coordinates as the primary key Call this primary key x The other coordinate, y, is the secondary tree This key is also used to sort the data 38 Point Quadtrees The first subdivision point is the median of the sorted data This insures that none of the children of the root node receives more than half the points 39 Point Quadtrees O(n) time will be used to sort the data contained in each of the four subregions The total work at every level of the tree is bounded by O(n) At most there will be O(log n) levels in the tree A height balanced quadtree can be built in O(nlogn) time 40 Point Quadtrees Search To search for a point, compare the point at the root with the point to find If the points are different, then the point to search for is used to determine where to go next 41 Point Quadtrees Search The search continues by recursively calling the search procedure with the subregion’s root as the root of the new tree to search The search stops if the point is found or if a leaf node is reached 42 Point Quadtrees Search The algorithm for search is O(h) where h is the height of the tree 43 Point Quadtrees Insertion Insertion is accomplished by search for the point in the tree The search will end at a leaf The leaf node now is a region that contains two points 44 Point Quadtrees Insertion The leaf node now is a region that contains two points One point is chosen of the two to subdivide the region The point becomes the child of the node representing the region where the point belongs 45 Point Quadtrees The run time for insertion is bounded by O(h) In d dimensions the run time is bounded by O(dh) 46 Point Quadtrees Deletion The node is located by search To delete the node it is necessary to locate another point that will take its place This is where the complexity of the algorithm for deletion lies 47 Region Quadtrees A region quadtree for n points in d dimensions is defined as follows: Consider that we have a hypercube large enough to enclose all of the points The region is represented by the root of the ddimensional quadtree 48 Region Quadtrees The region is subdivided into 2d subregions of equal size A subregion is subdivided by bisecting along each dimension Each of these regions containing at least one point is represented as a child of the root node 49 Region Quadtrees Each of the regions that contain at least one point is represented as the child of the root node The same procedure is recursively applied to each child of the root node The process is terminated when a region contains only a single point 50 Region Quadtrees This data structure is known as the point region quadtree or PR-quadtree 51 Region Quadtrees 52 2-D Polygonal Objects Suppose we restrict ourselves to 2-D polygonal objects If we recursively divide the tree nodes yields minimum size nodes all along the edges of the polygon The resulting tree is large and the number of nondivisible cells is proportional to the polygon’s perimeter 53 Algorithm The algorithm for building the tree from boundary information is simple Recognition of boundaries from the quadtree is complex The algorithm must infer straight edges from staircaselike contours 54 A Different Quadtree In this quadtree, EDGE nodes are considered, including WHITE nodes BLACK nodes GRAY nodes 55 EDGE Nodes Partly inside and partly outside the object The piece of the object boundary that is contained in the node is a simple straight segment 56 Features of Quadtrees (1) The resulting trees are more compact and shorter than the usual quadtree (2) The recomputation of the boundary model is easy and exact 57 Quadtree Representation The quadtree representation has two data structures First - a tree structure in which data is stored linearly by a depth method The second is a sequential list storing the edges that define the polygonal object boundary 58 An Example 59 Compact Representation We will be using a compact representation for the tree - a so-called list representation The primitive elements of the list will be X, W, G, B 60 Compact Representation W WHITE is used if the quadrant is entirely outside the object the node represents 61 Compact Representation B BLACK if the quadrant is entirely inside the object boundary 62 Compact Representation X EDGE if and only if one boundary edge and only one edge crosses the quadrant EDGE nodes have a second field storing a pointer to the edge crossing the quadrant 63 Compact Representation G A node is GRAY when more than one boundary edge crosses the quadrant Represent either terminal or non-terminal nodes 64 Compact Representation ((X(X(WWGW)XX)((WWWG)XWX)B)XX ((B(XXBG)BX)W(XXX(GWWW))W)) 65 Compact Representation The coding of quadrants is done in this order. ((X(X(WWGW)XX)((WWWG)XWX)B)XX ((B(XXBG)BX)W(XXX(GWWW))W)) 66