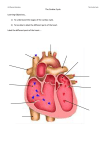
Download 4c Heart Physiology for lab

Cardiac Physiology for Lab
1
 Cardiac Output (CO)
 Blood pressure
 Vessel resistance
2
Blood Flow (L/min)
• Blood flow is the quantity of
blood that passes a given
point in the circulation in a
given period of time.
• Overall flow in the circulation
of an adult is 5 liters/min
which is the cardiac output.
• HR = heart rate
• SV = stroke volume (how
much blood is ejected from
the left ventricle)
• CO= HR X SV
• 70 b/min x 70 ml/beat
=4900ml/min
3
Ventricular Ejection Volume =
Stroke Volume
• Stroke Volume (SV)
– amount ejected, ~ 70 ml
• End Diastolic Volume (EDV)
~120 ml (max amount the left
ventricle can hold)
• SV/EDV= ejection fraction (what
percentage of blood is ejected
from the left ventricle)
EF = SV/EDV
70/120 = 58%
– at rest ~ 60%
– during vigorous exercise as
high as 90%
– diseased heart < 50%
• End-systolic volume: amount left
in heart (50ml)
120-70 = 50ml
4
Cardiac Output (CO)
• Amount ejected by a ventricle in
1 minute
• CO = HR x SV
• Resting values, 4- 6 L/min
• Vigorous exercise, 21 L/min
• Cardiac reserve: difference
between maximum and resting CO
If resting CO = 6 L/min and after exercise increases
to 21 L/min, what is the cardiac reserve?
CR = 21 – 6 L/min
CR = 15 L/min
5
Volumes and Fraction
•
•
•
•
End diastolic volume
= 120 ml
End systolic volume
= 50 ml
Ejection volume (stroke volume) = 70 ml
Ejection fraction = 70ml/120ml = 58%
(normally 60%)
• If heart rate (HR) is 70 beats/minute, what is
cardiac output?
• Cardiac output = HR * stroke volume
= 70/min. * 70 ml
6
= 4900ml/min.
Questions
• If EDV = 120 ml and ESV = 50 ml:
• What is the SV?
• 120-50 = 70 ml
• What is the EF?
• 70/120 = 58%
• What is the CO if HR is 70 bpm?
• 70/bpm * 70 ml = 4900ml/min.
7
Formulas to Know
• Cardiac Output
CO= HR X SV
• Cardiac Reserve
– If resting CO = 6 L/min and after exercise increases to
21 L/min, what is the cardiac reserve? CR = 21 – 6
L/min
• Stroke Volume
SV = (End diastolic volume) – (End systolic volume).
Normal is 120-50 = 70 ml
• Ejection Fraction
EF = SV/End diastolic volume.
Normal is 70/120 = 58%
8
Ohm’s Law Formulas
Q= P/R
P = QR
R = P/Q
•
•
•
Q is cardiac output
P is average blood pressure of the aorta
R is resistance in the blood vessels
9
Factors Affecting CO
• More blood viscosity (causes decreases CO)
• Total vessel length (longer decreases CO)
• Vessel diameter (larger increases CO)
10
Ohm’s Law
• Q=P/R
• Flow (Q) through a blood
vessel which is the same
thing as saying Cardiac
Output (CO) through the
heart, is determined by:
• 1) The pressure
difference (P) between
the two ends of the
circulatory tube (arteries
and veins)
– Directly related to flow
• 2) Resistance (R) of the
vessel
– Inversely related to flow
11
Clinical Significance
• Normal blood pressure is 120/80 mm Hg.
• 120 represents systolic pressure, and 80
represents diastolic pressure. The average of
these two pressures is 100 mm Hg
120 + 80 = 200
200/2 = 100 (the average)
• Therefore, the average pressure in the first
vessel leaving the heart (the aorta) is 100 mm
Hg.
• “100 mm Hg” means the amount of pressure
required to lift a column of mercury 100 mm in
the air. This is how the original blood pressure
cuffs work.
12
Clinical Significance
• In a normal person, the arterial pressure is
100 and the pressure in the veins is 0 (if
there were any pressure in the capillaries,
they would blow out, so blood pressure
drops to zero by the time it gets there, and
stays at zero in the veins.
• The pressure difference (P) is normally
100 – 0 = 100
Remember, Cardiac Output (CO) is normally
about 5 liters per minute.
13
Clinical Significance
• Therefore, applying Ohm’s Law (Q=P/R) to a
normal person, we get this:
5 = 100/R
Solving for R:
R = 100/5
R = 20 PRU
• That means that the normal amount of
resistance in the blood vessels is 20 PRU
(peripheral resistance units).
• Overall, the values for a normal person are:
5 = 100/20
14
Now let’s solve for  P (change in pressure)
instead of Q (cardiac output)
•
•
•
•
•
 P means subtracting the pressure in the veins (P2)
from the average pressure in the arteries (P1).
Therefore,  P = P1 – P2
Since P2 (blood pressure in the veins) is always 0, for
our purposes, you could just write P instead of  P.
P symbolizes blood pressure. Since BP is written
systolic/diastolic, you add up both pressures and take
the average.
The average person’s blood pressure is 120/80, so the
overall average pressure in the aorta is about 100 mm
Hg.
15
Clinical Significance:
Solve for Q (cardiac output)
• A person might have blood pressure higher than normal.
– They ate too much salt, so they are retaining water
• A patient has blood pressure of 140/100, yet their last
BP reading a few weeks ago was 120/80. When
questioned, the patient said they ate a lot of salt and
drank a lot of water yesterday.
• Problem: What is their cardiac output right now? We can
assume the resistance in their blood vessels is normal
since their BP was normal recently.
• Solution: First find the average arterial pressure
(140 + 100)/2 = 120
• Then apply Ohm’s Law (Q=P/R)
Q = 120/20
Q = 6 (Cardiac output increases)
The heart is pumping with more force than normal. Since it takes
more time to pump a larger bolus, the heart rate is slower.
16
Clinical Significance
• A person might have blood pressure lower than normal.
– They are dehydrated
• A patient has blood pressure of 60/40, yet their last BP
reading a few weeks ago was 120/80. When questioned,
the patient said they just got back from a hike and they
are thirsty.
• Problem: What is their cardiac output right now? We can
assume the resistance in their blood vessels is normal
since their BP was normal recently.
• Solution: First find the average arterial pressure
(60 + 40)/2 = 50
• Then apply Ohm’s Law (Q=P/R)
Q = 50/20
Q = 2.5 (Cardiac output decreases)
The heart is pumping with less force than normal. Since it
takes less time to pump a smaller bolus, the heart rate is faster.
17
Clinical Significance
• What is CO if you change the resistance?
• A patient might have higher vessel resistance if they
have clogged arteries (atherosclerosis) or calcium
deposits in the arteries (arteriosclerosis).
• Problem: What is the cardiac output in a patient with BP
of 120/80 and a higher than normal resistance? Let’s say
R = 30.
• Apply Ohm’s Law (Q=P/R)
Q = 100/30
Q = 3.3 (Cardiac output decreases)
The heart is pumping with less force than normal. Since it takes less time to
pump a smaller bolus, the heart rate is faster.
18
Clinical Significance
• Problem: What is the cardiac output in a patient with BP
of 120/80 and a lower than normal resistance, perhaps
they are athletes who have developed large arteries?
Let’s say R = 10.
• Apply Ohm’s Law (Q=P/R)
Q = 100/10
Q = 10 (Cardiac output increases)
The heart is pumping with more force than normal. Since it
takes more time to pump a larger bolus, the heart rate is
slower.
Therefore, someone with a slow heart rate and large cardiac
output might have a condition relating to low peripheral
resistance, such as an aerobic athlete.
19
Solve for P
• What would you expect the blood pressure
to be in a person who has increased
peripheral resistance (clogged arteries)?
Let’s say R = 50
P = QR
P = (5)(50)
P = 250 (normal would be 100)
The person would have high blood pressure.
20
Solve for P
• What would you expect the blood pressure
to be in a person who has decreased
peripheral resistance (athlete)? Let’s say
R = 10
P = QR
P = (5)(10)
P = 50 (normal would be 100)
The person would have low blood pressure.
21
Solve for P
• What would you expect the blood pressure
to be in a person who has increased
cardiac output (over-hydration)? Let’s say
Q=6
P = QR
P = (6)(20)
P = 120 (normal would be 100)
The person would have higher blood
pressure.
22
Solve for P
• What would you expect the blood pressure
to be in a person who has decreased
cardiac output (dehydration)? Let’s say Q
=4
P = QR
P = (4)(20)
P = 80 (normal would be 100)
The person would have lower blood
pressure.
23
Now let’s solve for R
• What would you expect the peripheral
resistance to be in a person who has
decreased cardiac output (dehydration)?
Let’s say Q = 4
R = P/Q
R = 100/4
R = 25 (normal would be 20)
The person would have higher than normal
resistance.
24
Solve for R
• What would you expect the peripheral
resistance to be in a person who has
increased cardiac output (over-hydration)?
Let’s say Q = 6
R = P/Q
R = 100/6
R = 16 (normal would be 20)
The person would have lower than normal
resistance.
25
Solve for R
• What would you expect the peripheral
resistance to be in a person who has
decreased blood pressure (athlete)? Let’s
say P = 80
R = P/Q
R = 80/5
R = 16 (normal would be 20)
The person would have low peripheral
resistance.
26
Solve for R
• What would you expect the peripheral
resistance to be in a person who has
increased blood pressure (clogged
arteries)? Let’s say P = 120
R = P/Q
R = 120/5
R = 24 (normal would be 20)
The person would have higher peripheral
resistance.
27