Download Quadratic Functions, Expressions, and Equations (Investigation 1) TOOLKIT:

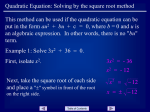
Math 2/Unit 5/Lesson 1 TOOLKIT:
Quadratic Functions, Expressions, and Equations (Investigation 1)
In this investigation, you gained experience in identifying functions and using function notation.
y = f(x) means y is a In this case, Run time (y-axis) is a function of vertical drop (x-axis)
function of x (the
equation is written in f(50) = 64 is the point (50, 64).
This means that for a vertical drop of 50 meters the time would be 64
terms of x)
seconds.
y = f(40) means to find the y-value when x = 40. The y-value of 71 can
be found by looking at the graph or at the table.
f(x) = 51 means to find x when the y-value is 51. The x-value of 80 can
be found by looking at the graph or at the table.
Function: y is a function of x when there is exactly one y-value that
corresponds to each x-value (Each x value has its own y-value)
Determining a function
from a table: All x
values in the table
should be different.
↓
↓
This not a function because a vertical drop of 20
has two different times (101 and 90)
Determining a function
by looking at a graph
The Vertical Line Test says that if a vertical line drawn anywhere on the
graph touches the curve exactly once the graph is a function. If the
vertical line drawn touches the graph in more than one spot the graph is
not a function.
These two graphs
are functions
Run time (y-axis) is a function of
Height (y-axis) is a function of
vertical drop (x-axis) because
time (x-axis) because a vertical
a vertical line would touch the curve line would only touch the curve
only once (Each x has its’ own y)
only once (Each x has its’ own y)
These two graphs
are not functions
Time (y-axis) is not a function of
height (x-axis) because a vertical
line would touch the curve more
than once
The height(y-axis) is not a
function of age (x-axis)
because a vertical line would
touch the curve more than
once.
Using a function in
function notation
where d is the distance from the source and I is the
intensity of sound.
Find the intensity when
d=1
When the distance is 1 meter, the Intensity is 8 watts per square meter
Find the intensity when
d=2
When the distance is 2 meters, the Intensity is 4 watts per square meter
8
d2
Find the length when I (d )
I(d) = .5
.5
8
d2
Substitute in .5 for I(d)
8
(d 2 )
2
d
.5(d 2 ) 8
( d 2 ) .5
.5(d 2 ) 8
.5
.5
2
d
16
d2
d
16
Mutliplty both side by d 2
Divide both sides by .5
Square root both side
4
d = 4 is the only practical solution because you cannot have a negative
distance (d cannot be -4)
Domain and Range
Domain: Input (x-values)
Domain: Input (x-values) - d
Range: Output (y-values)
Range: Output (y-values) - I
Practical Domain: The distances that make sense or the actual
values shown to you on the graph
Practical Range:
The Intensity’s that make sense or the
actual values shown to you on the graph
Practical Domain: [0, how far you could hear]
Practical Range: [0, highest intensity]
Theoretical Domain: The distances that are based on looking
at the equation or graphs
Theoretical Range: The Intensity’s that are based on looking
at the equation or graphs
Theoretical Domain: [farthest left, farthest right]
Theoretical Range: [lowest, highest]
Theoretical Domain: (-∞, 0) U (0, ∞)
Theoretical Range: (0, ∞)
I(p) = p(100 –p),
where p is the price
and I is the income
Income is a function of price because the graph is a parabola
that opens down, so the graph passes the vertical line test.
Income is a function of price because each price has its’ own
income.
I(20) = 1600
When the price is set at $20 the income is $1600.
Theoretical Domain: (-∞,∞)
Theoretical Range: (-∞,2500]
Practical Domain: [0, 100] Lowest Price to Highest Price
Practical Range: [0, 2500] Incomes that match the lowest
and highest price
Theoretical Domain
f(x) = 7 -3x
f(x) = x2 – 5
f(x) = 3x
D: (-∞,∞)
R: (-∞,∞)
D: (-∞,∞)
R: [-5, ∞)
D: (-∞,∞)
R: (0, ∞)
f(x) =
f(x) = -x2 +3
D: [0,∞)
R: (-∞,0)
D: (-∞,∞)
R: [-∞, 3]
f(x) =
D: (-∞,0) U (0,∞)
R: (-∞,0) U (0,∞)
Math 2/Unit 5/Lesson 1 TOOLKIT:
Quadratic Functions, Expressions, and Equations (Investigation 2)
In this investigation, you explored the ways in which factored forms, graphs, and intercepts are related for
quadratic functions.
Intercept Form of a
Quadratic
Find the equation of the blue graph below:
Y = a(x – p)(x – q)
a: the number that
tells you the shape
of parabola and its
direction (Is it wide
or narrow. Does it
open up or down)
p: x-intercept
q: x-intercept
You must always find
a, p, and q to write
the equation of a
parabola in intercept
form
x-intercepts are x = 0 and x = 6 and the maximum is (3, 9)
p = 0 and q = 6 or vice versa and x = 3 when y = 9
Y = a(x – p)(x – q)
y = a(x – 0)(x – 6)
9 = a(3 – 0)(3 – 6)
9 = a(3)(-3)
9 = -9a
-1 = a
y = -1(x – 0)(x – 6) = -x(x – 6) Quadratic equation in intercept
form
y = -x(x – 6) = -x2 + 6x Quadratic equation in standard
or expanded form
Practical Domain: [0, 6] Practical Range [0, 9]
Theoretical Domain: (-∞,∞) Theoretical Range: (-∞,9)
Intercept Form of a
Quadratic
Find the equation of the red graph below:
Y = a(x – p)(x – q)
a: the number that
tells you the shape
of parabola and its
direction (Is it wide
or narrow. Does it
open up or down)
p: x-intercept
q: x-intercept
You must always find
a, p, and q to write
the equation of a
parabola in intercept
form
x-intercepts are x = 4 and x = 10 and the maximum is (7, 9)
p = 4 and q = 10 or vice versa and x = 7 when y = 9
Y = a(x – p)(x – q)
y = a(x – 4)(x – 10)
9 = a(7 – 4)(7 – 10)
9 = a(3)(-3)
9 = -9a
-1 = a
y = -1(x – 4)(x – 10) Quadratic equation in intercept form
y = -1(x – 4)(x – 10)
y = -(x2 – 10x – 4x + 40) = -(x2 – 14x + 40) = -x2 + 14x - 40
Quadratic equation in standard or expanded form
Practical Domain: [4, 10] Practical Range [0, 9]
Theoretical Domain: (-∞,∞) Theoretical Range: (-∞,9)
Find the equation of
the quadratic
function in intercept
and
standard/expanded
form with x-int at
(2, 0) and y-int at
(0, 6)
p = 2 and q = 2
Y = a(x – p)(x – q)
y = a(x – 2)(x – 2)
6 = a(0 – 2)(0 – 2)
6 = a(-2)(-2)
6 = 4a
1.5 = a
y = 1.5(x – 2)(x – 2) Quadratic equation in intercept form
y = 1.5(x – 2)2 Opens up
y = 1.5(x – 2)(x – 2)
y = 1.5(x2 – 2x – 2x + 4) = 1.5(x2 –4x + 4) = 1.5x2 - 6x + 6
Quadratic equation in standard or expanded form
To find theoretical range you must know the y-value of the
vertex (minimum/maximum)
Since there is only one x-intercept that is also the vertex
Theoretical Domain: (-∞,∞) Theoretical Range: (6, ∞)
If a > 0 the graph opens up and you have a minimum
If a < 0 the graph opens down and you have a maximum
Find the equation of
the quadratic
function with x-int
at (4, 0) and (-1, 0)
Find the equation of
the quadratic
function with x-int
at (7, 0) and (1, 0)
and it opens up
Find the equation of
the quadratic
function with x-int
at (-5, 0) and (0, 0)
and it opens down
Find the equation of
the quadratic
function with x-int
at (0, 0)
Find the equation of
the quadratic
function with x-int
at (-3, 0) and it
opens up
p =4 and q = -1
y = a(x – p)(x – q)
y = a(x – 4)(x + 1) where a < 0 (opens down) or a > 0 (opens up)
p =7 and q = 1
y = a(x – p)(x – q)
y = a(x – 7)(x - 1) where a > 0 (opens up)
p =-5 and q = 0
y = a(x – p)(x – q)
y = a(x + 0)(x + 5)
y = ax(x + 5) where a < 0 (opens down)
p =0 and q = 0
y=
y=
y=
y=
a(x – p)(x – q)
a(x – 0)(x + 0)
a(x)(x)
ax2 where a < 0 (opens down) or a > 0 (opens up)
p =-3 and q = -3
y = a(x – p)(x – q)
y = a(x + 3)(x + 3)
y = a(x + 3)2 where a > 0 (opens up)
Graph the quadratic
function given in
intercept form
f(x) = (x + 3)(x – 1)
1.Find the x-int. by
taking the opposite
of what is in
parenthesis
x-intercepts: x = -3 (-3, 0) and x = 1 (1, 0)
(These numbers make the original equation equal zero)
2. To find the y-int
substitute x=0 into
the original equation
y-intercept
y = (0 + 3)(0 – 1) =(3)(-1) = -3
(0, -3)
3. To find the
vertex
(maximum/minimum)
find the xcoordinate halfway
between the xintercepts and
substitute that
number into the
original equation
x = -1 is halfway between x = -3 and x = 1
y = (x + 3)(x – 1)
y = (-1 + 3)(-1 – 1)
y = (2)(-2)
y = -4
Minimum(because a > 0) is (-1, -4)
4. Graph the x-int,
y-int, and vertex
5. Find the
theoretical
domain/range
Theoretical Domain: (-∞,∞) Theoretical Range: [-4, ∞)
Graph the quadratic
function given in
intercept form
y = -2(2 + x)(3 – x)
1.Find the x-int. by
taking the opposite
of what is in
parenthesis
x-intercepts: x = -2 (-2, 0) and x = 3 (3, 0)
(These numbers make the original equation equal zero)
2. To find the y-int
substitute x=0 into
the original equation
y-intercept
y = -2(2 + x)(3 – x)
y = -2(2 + 0)(3 – 0)
y = -2(2)(3) = -12
(0, -12)
3. To find the
vertex
(maximum/minimum)
find the xcoordinate halfway
between the xintercepts and
substitute that
number into the
original equation
x = .5 is halfway between x = -2 and x = 3
y = -2(2 + x)(3 – x)
y = -2(2 + .5)(3 – .5)
y = -2(2.5)(2.5)
y = -12.5
Minimum(because a < 0 and –x in parenthesis) is (.5, -12.5)
4. Graph the x-int,
y-int, and vertex
5. Find the
theoretical
domain/range
Theoretical Domain: (-∞,∞) Theoretical Range: [-12.5 , ∞)
Graph the quadratic
function given in
intercept form
y = .5(x - 6)2
1.Find the x-int. by
taking the opposite
of what is in
parenthesis
x-intercept: x =6 (6, 0)
(This number makes the original equation equal zero)
2. To find the y-int
substitute x=0 into
the original equation
y-intercept
y = .5(x - 6)2
y = .5(0 - 6)2
y = .5(36)
(0, 18)
3. To find the
vertex
(maximum/minimum)
find the xcoordinate halfway
between the xintercepts and
substitute that
number into the
original equation
Since there is only one x-intercept it is also the
minimum(because a > 0)
(6, 0)
4. Graph the x-int,
y-int, and vertex
5. Find the
theoretical
domain/range
Theoretical Domain: (-∞,∞) Theoretical Range: [0, ∞)
Graph the quadratic
function given in
intercept form
y = -2(2 + x)(3 – x)
1.Find the x-int. by
taking the opposite
of what is in
parenthesis
x-intercepts: x = -2 (-2, 0) and x = 3 (3, 0)
(These numbers make the original equation equal zero)
2. To find the y-int
substitute x=0 into
the original equation
y-intercept
y = -2(2 + x)(3 – x)
y = -2(2 + 0)(3 – 0)
y = -2(2)(3) = -12
(0, -12)
3. To find the
vertex
(maximum/minimum)
find the xcoordinate halfway
between the xintercepts and
substitute that
number into the
original equation
x = .5 is halfway between x = -2 and x = 3
y = -2(2 + x)(3 – x)
y = -2(2 + .5)(3 – .5)
y = -2(2.5)(2.5)
y = -12.5
Minimum(because a < 0 and –x in parenthesis) is (.5, -12.5)
4. Graph the x-int,
y-int, and vertex
5. Find the
theoretical
domain/range
Theoretical Domain: (-∞,∞) Theoretical Range: [-12.5 , ∞)
Graph the quadratic
function given in
intercept form
y = -x(x - 5)
1.Find the x-int. by
taking the opposite
of what is in
parenthesis
x-intercept: x =0 (0, 0) and x = 5 (5, 0)
(These numbers make the original equation equal zero)
2. To find the y-int
substitute x=0 into
the original equation
y-intercept
y = -x(x - 5)
y = -0(0 - 5)
y = 0(-5) = 0
(0, 0)
3. To find the
vertex
(maximum/minimum)
find the xcoordinate halfway
between the xintercepts and
substitute that
number into the
original equation
x = 2.5 is halfway between x = 0 and x = 5
y = -x(x - 5)
y = -2.5(2.5 - 5)
y = (-2.5)(-2.5)
y = 6.25
Maximum(because a < 0) is (2.5, 6.25)
4. Graph the x-int,
y-int, and vertex
5. Find the
theoretical
domain/range
Theoretical Domain: (-∞,∞) Theoretical Range: (-∞, 6.25]
Math 2/Unit 5/Lesson 1 TOOLKIT:
Quadratic Functions, Expressions, and Equations (Investigation 3)
In this investigation, you discovered strategies for expanding and factoring expressions that represent quadratic
functions.
Expanding Binomials
(FOIL)
F - First
O – Outer
I – Inner
L - Last
(x + 5)(x – 7) = x(x) + x(-7) + 5(x) + 5(-7)
= x2 – 7x + 5x - 35
= x2 -2x – 35
(x + 7)(2x + 3) = 2x2 + 3x + 14x + 21
= 2x2+ 17x + 21
(10 - x)(2 + x) = 20 + 10x -2x - x2
= 20 + 8x - x2
(5x - 3)(4 + 2x) = 20x + 10x2 + 3x -12 – 6x
= 10x2+ 14x - 12
(x + c) (x + d) = x2 + xd + xc + cd
Trinomial Squares
(x - 5)2 = (x - 5) (x - 5) = x2 - 5x - 5x + 25
= x2–10x + 25
(2x + 3)2 = (2x + 3) (2x + 3)= 4x2 + 6x + 6x + 9
= 4x2+ 12x + 9
(x + a)2 = (x + a) (x + a)= x2 + ax + ax + a2
= x2 + 2ax + a2
Difference of
Squares
(x + 10)(x – 10) = x2 – 10x + 10x - 100
= x2– 100
(x + 9)(x – 9) = x2 – 9x + 9x - 81
= x2– 81
(2x + 5)(2x – 5) = 4x2 – 10x + 10x - 25
= 4x2– 25
Factoring Using
Greatest Common
Factor
x2 + 8x = x(x + 8)
3x2 + 10x = x(3x + 10)
3x2 - 24x = 3x(x - 8)
9x2 - 15x = 3x(3x - 5)
Factoring
ax2 + bx + c
Using 2 Binomials
1. Write down 2
sets of parenthesis
2. Determine the
signs by looking at
the sign of the last
term only
3. List factors of
the last term. They
must add or
subtract to get the
middle term.
4. Check by
multiplying (smile)
x2 + 5x + 6 =
possible factors of 6: 1 and 6 or 2 and 3
x2 + 5x + 6 = (x + 2) (x + 3) Check: x(3) + 2(x) = 5x
x2 + 6x + 8 =
possible factors of 8: 1 and 8 or 2 and 4
x2 + 6x + 8 = (x + 4) (x + 2) Check: x(2) + 4(x) = 6x
x2 - 5x + 6 =
possible factors of 6: 1 and 6 or 2 and 3
x2 - 5x + 6 = (x - 2) (x - 3) Check: x(-3) + -2(x) = -5x
x2 - 8x + 15 =
possible factors of 15: 1 and 15 or 5 and 3
x2 - 8x + 15 = (x - 5) (x - 3) Check: x(-3) + -5(x) = -8x
If the last term is positive the signs in the binomials are the
same as the sign of the middle term
x2 - 2x - 8 =
possible factors of 8: 1 and 8 or 2 and 4
x2 - 2x - 8 = (x + 2) (x - 4) Check: x(-4) + 2(x) = -2x
x2 + 2x - 8 =
possible factors of 8: 1 and 8 or 2 and 4
x2 + 2x - 8 = (x + 4) (x - 2) Check: x(-2) + 4(x) = 2x
x2 + 3x - 28 =
possible factors of 28: 1 and 28 or 2 and 14 or 4 and 7
x2 + 3x - 28 = (x + 7) (x - 4) Check: x(-4) + 7(x) = 3x
x2 - x - 12 = x2 - 1x - 12
possible factors of 12: 1 and 12 or 2 and 6 or 4 and 3
x2 - 1x - 12= (x + 3) (x - 4) Check: x(-4) + 3(x) = -1x
If the last term is negative the signs in the binomials are
always one positive (+) and one negative (-)
The bigger of the two possible factors always gets the sign of
the middle term
Factoring a
Difference of
Squares
x2 - 100 =
square root of 100 is 10 and -10:
x2 - 100 = (x + 10) (x - 10) Check: x(-10) + 10(x) = 0x
If the last term is negative the signs in the binomials are
always one positive (+) and one negative (-)
The factors are always the square roots of the last term
x2 - 25 =
square root of 25 is 5 and -5:
x2 - 25 = (x + 5) (x - 5) Check: x(-5) + 5(x) = 0x
x2 - 20 =
square root of 20 is √20 and -√20:
x2 - 20 = (x + √20) (x - √20) Check: x(-√20) + √20 (x) = 0x
9x2 - 64 =
square root of 9 is 3 and -3: square root of 64 is 8 and -8:
9x2 - 64 = (3x + 8) (3x - 8) Check: 3x(-8) + 8(3x) = 0x
Difference of
Squares
x2 - 36 =
square root of 36 is 6 and -6:
x2 - 36 = (x + 6) (x - 6) Check: x(-6) + 6(x) = 0x
Difference of
Squares
36 - x2 =
square root of 36 is 6 and -6:
36 - x2 = (6 + x) (6 - x) Check: 6(-x) + x(6) = 0x
Not factorable with
real numbers
x2 + 36 = No Real Factors
Greatest Common
Factor
x2 – 36x = x(x-36)
Factoring a trinomial x2 + 10x + 25 =
square
square root of 25 is 5:
x2 + 10x + 25 = (x + 5) (x +5) Check: x(5) + 5(x) = 10x
1st and last terms
x2 + 10x + 25 = (x + 5)2
are perfect squares
Make sure you still
x2 - 18x + 81 =
check you smile
square root of 81 is 9:
x2 - 18x + 81 = (x - 9) (x - 9) Check: x(9) + 9(x) = 18x
The last term is
x2 - 18x + 81 = (x - 9)2
always positive in a
trinomial square, so
4x2 + 4x + 1 =
the signs are always square root of 4 is 2:
the same as the
4x2 + 4x + 1 = (2x + 1) (2x + 1) Check: 2x(1) + 1(2x) = 4x
middle term.
4x2 + 4x + 1 = (2x + 1)2
4x2 - 28x + 49 =
square root of 4 is 2 and square root of 49 is 7:
4x2 - 28x + 49 = (2x + 7) (2x + 7) Check: 2x(7) + 7(2x) = 28x
4x2 - 28x + 49 = (2x + 7)2
Why do we factor?
So we can graph the
function
y = x2 + 8x +12
1. Factor the given
equation
y = (x + 6)(x + 2)
2. Find the x-int. by
taking the
opposite of what
is in parenthesis
3. To find the y-int
substitute x=0
into the original
equation
x-intercept: x =-6 (-6, 0) and x = -2 (-2, 0)
(These numbers make the original equation equal zero)
4. To find the
vertex
(maximum/minimu
m) find the xcoordinate
halfway between
the x-intercepts
and substitute
that number into
the original
equation
5. Graph the x-int,
y-int, and vertex
6. Find the
theoretical
domain/range
x = -4 is halfway between x = -6 and x = -2
y = (x + 6)(x + 2)
y = (-4 + 6)(-4 + 2)
y = (2)(-2)
y = -4
Maximum(because a < 0) is (-4, -4)
y-intercept
y = x2 + 8x +12
y = 02 + 0x +12 = 12
(0, 12)
Theoretical Domain: (-∞,∞) Theoretical Range: [-4, -∞)
Factoring
ax2 + bx +c
The only factoring
rule that stays the
same is how you find
the signs.
After that you must
guess and most
importantly check.
2x2 - 3x - 20 =
Possible factors for 2x2: 2x and x
Possible factors for 20: 20 and 1: 10 and 2: 5 and 4
2x2 - 3x - 20 = (2x + 5)(x – 4)
Check: 2x(-4) + 5(x) = -3x
3x2 - 12x + 12 =
Possible factors for 3x2: 3x and x
Possible factors for 12: 12 and 1: 6 and 2: 3 and 4
3x2 - 12x + 12 = (3x -6)(x – 2)
Check: 3x(-2) + -6(x) = -12x
14x2 - 19x - 40 =
Possible factors for 14x2: 7x and 2x: 14x and x
Possible factors for 40: 40 and 1: 20 and 2: 10 and 4: 8 and 5
14x2 - 19x - 40 = (7x + 8)(2x – 5) Check: 7x(-5) + 8(2x) = -19x
The rules of factoring (Summary)
First check to see if you are trying to factor a binomial or a
trinomial
If it is a binomial:
1)
2)
Look for the greatest common factor
Look for a difference of squares.
1)
This means that the two terms of the binomial are perfect squares and
there is a minus sign between them.
You are done factoring a binomial:
1)
2)
3)
When there is an addition sign, or
When there are no more perfect squares, or
When there is no longer a squared term
If it is a trinomial:
1)
2)
3)
4)
5)
Look for the greatest common factor
Determine what the signs are
1)
If the last term is positive the signs are both the same as the middle
term
2)
If the last term is negative the signs are opposites(one is positive and
one is negative)
Look at the first term. If there is not a number in front of the squared term
then you only need to look at factors of the last term that will add or subtract
to get the middle term
Look at the first term. If there is a number in front of the squared term, you
must look at factors of the first term and of the last term. In this situation you
must always guess and check.
Always factor completely
Math 2/Unit 5/Lesson 1 TOOLKIT:
Quadratic Functions, Expressions, and Equations (Investigation 4)
In this investigation, you developed strategies for solving quadratic equations by algebraic reasoning without the
aid of calculator or computer tables, graphs, or symbol manipulation programs.
Solving quadratic
equations using square
roots
Use when the only
variable term is x2
5x2 + 12 = 57
-12 -12
2
5x = 45
x2 = 9
x = ±3
8 - 2x2 = x2 + 5
+ 2x2 +2x2
8 = 3x2 + 5
-5
-5
2
3 = 3x
1 = x2
x = ±1
Solving using
x(x – 5) = 0
Greatest common
x=0 x=5
factor when there is
x2 and x.
5x2 + 15x = 0
5x(x + 3)
You must have the
x=0 x=5
equation set = 0
16x - 4x2 = 0
4x(4 - x)
x=0 x=4
3x + 5x2 = -7x
+7x
+7x
2
10x + 5x = 0
5x(2 + x)
x = 0 x = -2
Solving by factoring
These equations will
have x2, x, and a
constant.
They must also be
set = 0 before you
factor
There are two ways
to solve this one
x2 + 2x - 24 = 0
(x + 6)(x – 4) = 0
x = -6 x = 4
-x2 + 8x - 15 = 0
(-x2 + 8x - 15 = 0 )-1
x2 - 8x + 15 = 0
(x - 5)(x – 3) = 0
x=5 x=3
2x2 - 12x + 18 = 0
(2x – 6)(x – 3) = 0
x=3
Check: 2x(-3) + -6(x) = -12x
OR
2x2 - 12x + 18 = 0
2
2
2 2
2
x - 6x + 9 = 0
(x – 3)(x – 3) = 0
x=3
When you solve a
quadratic equation
you are finding the
x-intercepts of the
parabola
Check: x(-3) + -3(x) = -6x
Math 2/Unit 5/Lesson 2 TOOLKIT:
Nonlinear Systems of Equations (Investigation 1)
In this investigation, you developed strategies for solving problems that involve both a linear function and an
inverse variation function.
What strategies are useful in
solving problems that involve
links between two
functions—one a linear
function and one an inverse
variation function?
Provide an example that has
two solutions.
Math 2/Unit 5/Lesson 2 TOOLKIT:
Nonlinear Systems of Equations (Investigation 2)
In this investigation, you developed strategies for solving problems that involve combinations of linear and
quadratic functions.
What strategies are effective
in solving a system that
consists of one linear and
one quadratic function?
Provide an example that has
two solutions.
Math 2/Unit 5/Lesson 3 TOOLKIT:
Common Logarithms and Exponential Equations (Investigation 1)
In work on the problems of this investigation, you learned how physical measurements of sound intensity and
acidity of a chemical substance are converted into the more familiar decibel and pH numbers. You also learned
how the logarithm function is used in those processes.
Record the definition of a
logarithm and two examples.
Then explain in your own
words what log y = x means.
Math 2/Unit 5/Lesson 3 TOOLKIT:
Common Logarithms and Exponential Equations (Investigation 2)
In work on the problems of this investigation, you learned how to use logarithms to solve equations related to
exponential functions.
Provide examples of how to
use logarithms to solve
equations of the form
a(10mx + n) = c.