Download Proof of SSS from SAS (Word)

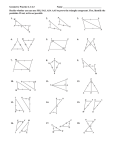
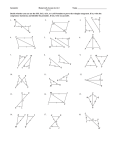
Absolute geometry
Congruent triangles - SAS, ASA, SSS
Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section
3.3, pp 139-150. The problems are all from section 3.3.
Proving SSS from SAS (fill in and submit as GR5 – part 2)
SSS Theorem
If, under some correspondence between their vertices, two triangles have the three sides of one
congruent to the corresponding three sides of the other, then the triangles are congruent under
that correspondence. [Kay, p 141]
PICTURE
CONCLUSIONS
JUSTIFICATIONS
Suppose you have two triangles Hypothesis (Given)
which satisfy the hypothesis of
SSS: three sides of one
congruent to the corresponding
three sides of the other.
The goal is to show that having SSS (thing you want to prove) always leads to having SAS (the postulate);
i.e. having the corresponding parts congruent that are marked below:
always leads to having the additional marked angles congruent:
which then allows us to conclude the triangles are congruent by the SAS Postulate (which we assume as
the basis for this geometry). This establishes SSS as a theorem; if we start with the SSS hypothesis (“two
triangles have the three sides of one congruent to the corresponding three sides of the other”), then the
conclusion is the triangles must be congruent.
The trick in this one is to construct a copy XYZ onto ABC , and show that the copy is congruent to
ABC . This is a slightly simplified version - you can use the betweenness relations apparent in the
figures. Also assume that the figures are oriented so that the angles at the base are acute (i.e., if this
were an obtuse triangle, I'd orient it with the obtuse angle at the top).
PICTURE
CONCLUSIONS
AB  XY
BC  YZ
CA  ZX
Copy X and Z onto
JUSTIFICATIONS
Hypothesis (Given)
[Fill in 1]
segment AB , as shown
with the vertices at A
and C .
ADC  XYZ
This gives AD  XY and
therefore AD  AB ,
and also [Fill in 3]
[Fill in 2]
[Fill in 4]
(At this point you can
ignore XYZ for a
while.) Construct
[Fill in 5]
segment BD .
What can you conclude
about DAB (what type
of triangle is it and why)?
[Fill in 6]
[Fill in 7]
Therefore, what do you
know about ABD and
ADB ?
[Fill in 8]
[Fill in 9]
Make similar statements
about BCD (you can
condense the two steps
into one here).
[Fill in 10]
[Fill in 8] and [Fill in 9],
as above
Assuming betweeness as
apparent…
[Fill in 11]
(you could throw in a
couple extra steps and
the Crossbar theorem,
but just go straight to ...)
Angle addition postulate
Make a statement about
angles  B and D :
[Fill in 12]
[Fill in 13]
And conclude with the
triangles
[Fill in 15]
[Fill in 14]
Which now gets us the SSS Theorem; if we assume SSS, we eventually get to SAS, so SSS is sufficient to
show triangles congruent. Notice we also used the previously established ASA theorem along the way.