Download BEI06_ppt_0507

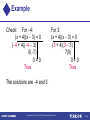
Chapter 5
Polynomials and
Factoring
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5.7
Solving Quadratic Equations
by Factoring
• The Principle of Zero Products
• Factoring to Solve Equations
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-2
Second degree equations like 9t2  4 = 0 and x2 +
6x + 9 = 0 are called quadratic equations.
Quadratic Equation
A quadratic equation is an equation
equivalent to one of the form
ax2 + bx + c = 0,
where a, b, and c are constants, with a ≠ 0.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
The Principle of Zero Products
An equation AB = 0 is true if and only if
A = 0 or B = 0, or both.
(A product is 0 if and only if at least
one factor is 0.)
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
Example
Solve: (x + 4)(x  3) = 0
Solution
In order for a product to be 0, at least one factor
must be 0. Therefore, either
x + 4 = 0 or
x3=0
We solve each equation:
x+4=0
or x  3 = 0
x = 4 or
x=3
Both 4 and 3 should be checked in the original
equation.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-5
Example
Check: For 4:
(x + 4)(x  3) = 0
(4 + 4)(4  3)
0(7)
0=0
True
For 3:
(x + 4)(x  3) = 0
(3 + 4)(3  3)
7(0)
0=0
True
The solutions are 4 and 3.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-6
Example
Solve: 4(3x + 1)(x  4) = 0
Solution Since the factor 4 is constant, the only way for
4(3x + 1)(x  4) to be 0 is for one of the other factors to be 0.
That is,
3x + 1 = 0
or
x4=0
3x = 1
or
x=4
1
x = 4.
x
3
Check: For 1/3:
4(3x + 1)(x  4) = 0
4(3  1) + 1)( 1  4)
= 0
3
3
4(0)( 4 13 ) = 0
0=0
For 4:
4(3x + 1)(x  4) = 0
4(3(4) + 1)(4  4) = 0
4(13)(0) = 0
0=0
The solutions are 1/3 and 4.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-7
Example
Solve: 3y(y  7) = 0
Solution
3  y(y  7) = 0
y=0
or
y=0
or
y7=0
y =7
The solutions are 0 and 7. The check is left to the
student.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-8
Factoring to Solve Equations
By factoring and using the principle of zero products, we
can now solve a variety of quadratic equations.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-9
Example
Solve: x2 + 9x + 14 = 0
Solution
This equation requires us to factor the polynomial
since there are no like terms to combine and there
is a squared term. Then we use the principle of zero
products:
x2 + 9x + 14 = 0
(x + 7)(x + 2) = 0
x+7=0
or x + 2 = 0
x = 7
or
x = 2.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-10
Example
Check: For 7:
x2 + 9x + 14 = 0
(7)2 + 9(7) + 14 0
49  63 + 14
14 + 14
0=0
True
For 2:
x2 + 9x + 14 = 0
(2)2 + 9(2) + 14 0
4 18 + 14
14 + 14
0=0
True
The solutions are 7 and 2.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-11
Example
Solve: x2 + 9x = 0
Solution Although there is no constant term,
because of the x2-term, the equation is still
quadratic. Try factoring:
x2 + 9x = 0
x(x + 9) = 0
x=0
or
x+9=0
x=0
or
x = 9
The solutions are 0 and 9. The check is left to the
student.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-12
Caution! We must have 0 on one side of the
equation before the principle of zero products can
be used. Get all nonzero terms on one side and 0
on the other.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-13
Example
Solve: x2  12x = 36
Solution We first add 36 to get 0 on one side:
x2  12x = 36
x2  12x + 36 = 36 + 36
(x  6)(x  6) = 0
x  6 = 0 or
x6=0
x = 6 or
x=6
There is only one solution, 6.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-14
Example
Solve: 9x2 = 49
Solution
9x2 = 49
9x2  49 = 0
(3x  7)(3x + 7) = 0
3x  7 = 0 or 3x + 7 = 0
3x = 7 or
3x = 7
7
x
3
7
x
3
7
7
The solutions are and  .
3
3
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-15
Example
Solve: 14x2 + 9x + 2 = 10x + 6
Solution Be careful with an equation like this! Since we
need 0 on one side, we subtract 10x and 6 from the
right side.
14x2 + 9x + 2 = 10x + 6
14x2 + 9x  10x + 2  6 = 0
14x2  x  4 = 0
(7x  4)(2x + 1) = 0
7x  4 = 0 or 2x + 1 = 0
7x = 4 or
2x = 1
x = 4/7 or
x = 1/2
The solutions are 4/7 and 1/2.
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
5-16
Example
Find the x-intercepts for the graph of the
equation shown. (The grid is intentionally
not included)
Solution
To find the intercepts, we let y = 0 and
solve for x.
0 = x2 + 2x  8
0 = (x + 4)(x  2)
x+4=0
or x  2 = 0
x = 4 or
x=2
The x-intercepts are (4, 0) and (2, 0).
Copyright © 2014, 2010, and 2006 Pearson Education, Inc.
y = x2 + 2x  8
5-17