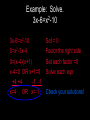* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 5.2: Solving Quadratic Equations by Factoring
Equations of motion wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Differential equation wikipedia , lookup
Equation of state wikipedia , lookup
Itô diffusion wikipedia , lookup
Calculus of variations wikipedia , lookup
Partial differential equation wikipedia , lookup
5.2: Solving Quadratic Equations by Factoring (p. 256) To solve a quadratic eqn. by factoring, you must remember your factoring patterns! Zero Product Property • Let A and B be real numbers or algebraic expressions. If AB=0, then A=0 or B=0. • This means that If the product of 2 factors is zero, then at least one of the 2 factors had to be zero itself! Example: Solve. x2+3x-18=0 x2+3x-18=0 (x+6)(x-3)=0 x+6=0 OR x-3=0 -6 -6 +3 +3 x=-6 OR x=3 Factor the left side set each factor =0 solve each eqn. check your solutions! Example: Solve. 2t2-17t+45=3t-5 2t2-17t+45=3t-5 2t2-20t+50=0 2(t2-10t+25)=0 t2-10t+25=0 (t-5)2=0 t-5=0 +5 +5 t=5 Set eqn. =0 factor out GCF of 2 divide by 2 factor left side set factors =0 solve for t check your solution! Example: Solve. 3x-6=x2-10 3x-6=x2-10 0=x2-3x-4 0=(x-4)(x+1) x-4=0 OR x+1=0 +4 +4 -1 -1 x=4 OR x=-1 Set = 0 Factor the right side Set each factor =0 Solve each eqn. Check your solutions! Finding the Zeros of an Equation • The Zeros of an equation are the xintercepts ! • First, change y to a zero. • Now, solve for x. • The solutions will be the zeros of the equation. Example: Find the Zeros of y=x2-x-6 y=x2-x-6 0=x2-x-6 0=(x-3)(x+2) x-3=0 OR x+2=0 +3 +3 -2 -2 x=3 OR x=-2 Change y to 0 Factor the right side Set factors =0 Solve each equation Check your solutions! If you were to graph the eqn., the graph would cross the x-axis at (-2,0) and (3,0). Assignment