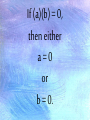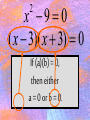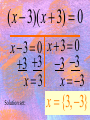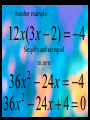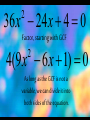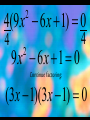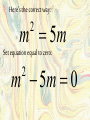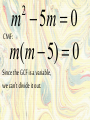Download Solving Quadratic Equations by Factoring

Solving Quadratic
Equations
by Factoring
In
Algebra County
A quadratic equation
is an equation that
has a squared term
in it. Sometimes it is difficult to recognize
until you start
simplifying it.
For example:
5 x  45  0
2
This tells us that we have
a quadratic equation.
There is a property that we need
to understand in order to solve
these equations by factoring.
It is called the “Multiplication Property
of Zero.”
It says that if two numbers multiply to
zero, one of them has to be zero.
If (a)(b) = 0,
then either
a=0
or
b = 0.
Return to our problem:
5 x  45  0
2
In order to use the
multiplication property
of zero, we set the
equation equal to zero.
Then we factor
5 x  45  0
2
5( x  9)  0
5
5
2
x 9  0
2
x 9  0
( x  3)( x  3)  0
2
If (a)(b) = 0,
then either
a = 0 or b = 0.
( x  3)( x  3)  0
x 3  0 x  3  0
3 3 3 3
x 3
x  3
Solution set:
x  {3, 3}
Another example:
12 x(3x  2)  4
Simplify and set equal
to zero:
36 x  24 x  4
2
36 x  24 x  4  0
2
36 x  24 x  4  0
2
Factor, starting with GCF
4(9 x  6 x  1)  0
2
As long as the GCF is not a
variable, we can divide it into
both sides of the equation.
4(9 x  6 x  1)  0
2
4
9x  6x 1  0
2
4
Continue factoring:
(3x  1)(3 x  1)  0
(3x  1)(3 x  1)  0
3x 1  0
Add 1:
3x  1
3 3
Same as on
left side.
1
x
3
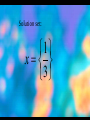
Solution set:
1 
x 
3
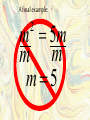
A final example:
m  5m
m m
m5
2
Here’s the correct way:
m  5m
2
Set equation equal to zero:
m  5m  0
2
m  5m  0
CMF:
m(m  5)  0
2
Since the GCF is a variable,
we can’t divide it out.
m(m  5)  0
m
5

0
m

0
Add 5:
That’s one
answer.
m5
Solution set:
m  {0,5}
STEPS
• Simplify
• Set equal to zero, in descending
order
• Factor
• Make big T and get two answers