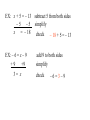Download Lesson 1.1

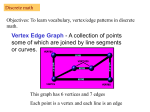
Lesson 1.1
Objective: To solve one step equations
Essential Question: How does understanding
inverse operations help solve one step
equations?
Vocab:
Inverse operations:
Are operations that undo each
other such as addition and
subtraction.
Isolating the Variable: means to get the variable
by itself.
Properties of Equality
Addition/Subtraction Property of Equality:
Adding or Subtracting the same number
from each side of an equation produces an
equivalent equation.
If a = b, then a + c = b + c
If a = b then a – c = b – c
Multiplication/ Division Property of Equality:
Multiplying or Dividing the same
number from each side of an equation
produces an equivalent equation.
If a = b, then a ∙ c = b ∙ c
If a = b, then a ÷ c = b ÷ c
c≠0
EX: x + 5 = – 13 subtract 5 from both sides
–5
– 5 simplify
x = – 18
check
– 18 + 5 = – 13
EX: – 6 = x – 9
+9
+9
3= x
add 9 to both sides
simplify
check
–6=3–9
EX: 7 – x = 42
–7
–7
– x = 35
+x
+x
0 = 35 + x
– 35 –35
– 35 = x
subtract 7 from both sides
we are solving for x not – x.
add x to both sides
subtract 35 from both sides
check
7 – (– 35) =42
We could of solved – x = 35 by dividing both sides by –1
The temperature in Anchorage Alaska fell from 17degrees at
6:00p.m. to – 6 degrees at 6:00a.m.
Find how many degrees the temperature fell.
T = temperature change
17degrees + temperature change = new temperature
17 + T = – 6
– 17
– 17
T = – 23
Subtract 17 from both sides
The temperature fell 23 degrees
EX:
x
= 32
Multiply both sides by – 4
solve – 4
(– 4) x = 32 (– 4)
The -4’s cancel
–4
x = – 128
check – 128 = 32
–4
EX: solve
3
2 x Multiply each side by – —
6 = –—
3
2
3
Why – —
2 ? The reciprocal of –2/3 is – 3/2
2
– 3 • 6 = –
3
2
–9=x
•– 3
2
x
Check: - 2/3• –9 = 6
Practice: Solve each equation
1) –3x = 27
–3
2)
–3
x
 10
4
x
4   10  4
4
3)
X = –9
X= 40
1
x 8
4
4 1
4
 x  8
1 4
1
X = 32
Discrete math:
Vocabulary:
Hamiltonian Circuit/Paths:
A Hamiltonian path in a graph is a path that
passes through every vertex in the graph exactly
once. A Hamiltonian path does not necessarily pass
through all the edges of the graph, however.
A Hamiltonian path which ends in the same place in
which it began is called a Hamiltonian circuit.
Trace a Hamiltonian path
Only a path, not a circuit. The path did
not end at the same vertex it started.
The path does not need to go over every edge but it can only go
over an edge once and must pass through every vertex exactly
once.
Hamiltonian Circuits
are often called the
mail man circuit
because the mailman
goes to every mailbox
but does not need to go
over every street.
Video
Store
Home
Sweet
Home
Find the quickest
route from home
to the pharmacy
5
6
N
3
Bank
4
4
3
4
Dry
Cleaners
Grocery
Store
6
6
2
4
5
Pharmacy
Post Office
A weighted edge has a value assigned to the edge
(i.e.- miles, time, gallons of gas, any unit of measure)
Review:
Euler Graphs
Hamiltonian
Graphs
Circuits
Passes over edge exactly once. May pass
through a vertex more than once.
Passes through every vertex exactly once but
not necessarily over every edge.
The path ends at the same vertex it started.