* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download document
Unification (computer science) wikipedia , lookup
Kerr metric wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Perturbation theory wikipedia , lookup
Calculus of variations wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Equations of motion wikipedia , lookup
BKL singularity wikipedia , lookup
Differential equation wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
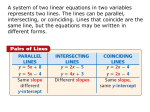
MTH 070 Elementary Algebra Chapter 4 – Linear Systems of Equations and Inequalities 4.1 The Graphing Method Copyright © 2010 by Ron Wallace, all rights reserved. Product Costs/Revenue x = number of items produced and sold Costs Fixed = $1500 Materials = $7/item Packaging = $1/item Shipping = $6/dozen Labor = $10/item Revenue Price = $40/item R 40x ? C 18.50x 1500 (70, 2800) ? (69.8, 2790.7) 500 10 System of Equations A set of two or more (related) equations. Solution – Values for the variables that satisfy every equation in the system. Example – Which of the following ordered pairs is a solution to the system … x 2 y 5 y x7 (8,1) (3, 1) (3, 4) (4,3) System of Equations A set of two or more (related) equations. Solution – Values for the variables that satisfy every equation in the system. Example – Which of the following ordered pairs is a solution to the system … y x 2 y 2x 2 2 ( 2, 2) (0, 2) (2, 2) (1, 0) Systems of Linear Equations in Two Variables Equations, when graphed, are lines. Ax + By = C y = mx + b x = ny + a y=b x=a (standard form) (slope-intercept form) (not common, but possible) (equivalent to y = 0x + b) (equivalent to x = 0y + a) How many solutions? Remember: The graph represents ALL solutions! Solving Systems by Graphing Basic Procedure: 1. 2. 3. 4. Graph both equations. Determine the point of intersection (it’s the solution). Write the solution as an ordered pair. Check the solution. It MUST work in BOTH equations. Limitation of this method? Accuracy (works okay w/ integer solutions and small numbers) Three Possibilities One Solution – The lines intersect at one point. Different slopes Three Possibilities One Solution – The lines intersect at one point. Different slopes No Solution – The lines do not intersect. Parallel lines Same slopes Different y-intercepts Three Possibilities One Solution – The lines intersect at one point. No Solution – The lines do not intersect. Different slopes Parallel lines Same slopes Different y-intercepts Many Solutions – The lines coincide. Equivalent equations Same slopes and intercepts. Consistent Systems A system that has at least one solution. Lines intersecting at one point. Lines that coincide. No Solution Inconsistent Independent Systems A system where the equations are NOT equivalent. Lines intersecting at one point. Parallel lines. Equivalent Equations Dependent Three Possibilities – Revisited One Solution – The lines intersect at one point. No Solution – The lines do not intersect. Consistent & Independent Inconsistent & Independent Many Solutions – The lines coincide. Consistent & Dependent