Download Ch 7 Alg 1 07

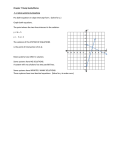
Tess McMahon
What is a Linear System?
 A linear system is two or more linear equations that
use the same variables
Ex:


X + 2y = 5
2x – 3y = 3
Equation 1
Equation 2
 The solution of the linear system is a pair of numbers
(a = x and b = y) that make BOTH equations true
How to Solve Linear Equations
 Graphing
 Substitution
 Linear Combinations
Graphing a Linear System
 Graph both equations on the same graph
Equation 1
x + 2y = 5
Equation 2
2x – 3y = 3
 The point where the graphs cross each other is the
solution of the equation
POINT OF INTERSECTION: (3, 1)
Solving Linear Systems by Substitution
Step-by-Step
The Equations:
–
–
Equation 1: x + 2y = 5
Equation 2: 2x – 3y = 3
Step 1
1. Put x and y on opposite sides of the equal sign in
Equation 1
x + 2y = 5
-2y -2y
x = 5 – 2y
Step 2
2. Substitute the x in Equation 2 with the answer you
found in step 1. You want to get rid of the x’s to solve
for y:
2x – 3y = 3
2(5 – 2y) – 3y = 3
10 - 4y - 3y = 3
10 – 7y = 3
- 10
- 10
-7y = -7
-7 -7
Y=1
Step 3
3. Plug in the value of y from Equation 2 into Equation 1
to solve for x:
x + 2y = 5
x + 2 (1) = 5
x+2=5
- 2 -2
x=3
The Solution:
(3,1)
Linear Combinations
In linear combinations, we must:
1. Multiply both equations by a constant (if necessary)
2. Add the resulting equations
Basically, the goal is to use addition to cancel out a
variable (y or x) to solve the linear system
Steps in Linear Combinations
Without Having to Multiply
1.


Write both equations:
Equation 1: 4x +3y = 16
Equation 2: 2x – 3y = 8
Steps in Linear Combinations Without
Having to Multiply
2. Add the equations together to get rid of y. Because the
constant before y in Equation one is 3 and the constant
before y in Equation two is -3, when you add them
together, y is cancelled out.
4x + 3y = 16
+ 2x – 3y = 8
6x = 24
x=4
Steps in Linear Combinations Without
Having to Multiply
3. Plug in 4 for the value of x in Equation 1 (you
could also use Equation 2). Now you are trying to
find the value of y.
4x + 3y = 16
4(4) + 3y = 16
16 + 3y = 16
-16
-16
3y = 0
y=0
Solution
(4, 0)
Steps in Linear Combinations that Involve
Multiplication
1.
Write both equations:


2.
Equation 1: 6x + 2y = 2
Equation 2: -3x + 3y = -9
If you look at the two, you’ll notice that if you
multiply Equation 2 by 2, the constant before x will
equal -6.
Steps in Linear Combinations that Involve
Multiplication
3. Multiply Equation 2 by 2 so that the x-intercept will
cancel out:
6x + 2y = 2
2(-3x + 3y) = (-9)2
Equation 1: 6x + 2y = 2
Equation 2 (Modified): -6x + 6y = -18
Steps in Linear Combinations that Involve
Multiplication
4. Now add the new Equation 2 and the old Equation 1 to
get rid of x:
6x + 2y = 2
+(-6x + 6y = -18)
8y = - 16
8
8
y = -2
Steps in Linear Combinations that Involve
Multiplication
5. Plug -2 in for y in Equation 1. Now you are trying
to find the value for x.
6x + 2y = 2
6x + 2(-2) = 2
6x - 4 = 2
+4 +4
6x = 6
x=1
Solution
(1, -2)
How Can We Use Linear Systems?
One of the reasons we use linear systems is to solve
word problems.
Solving Word Problems Using Linear
Combinations
Example: You combine 2 solutions to form a mixture
that is 40% acid. One solution is 20% acid (solution
A) and the other is 50% acid (solution B). If you
have 90 ml of the mixture, how much of each
solution was mixed?
Solving Word Problems Using Linear
Combinations
Before you freak out, figure out what they are looking
for: ‘how much’ = VOLUME.
Therefore, x and y must be the volumes of solution A
and solution B.
Volume of Solution A  x
Volume of Solution B  y
Volume of Solution A and Solution B = 90 ml
So, you’re first equation is: x + y = 90
Solving Word Problems Using Linear
Combinations
The other equation will be about the other part of
the problem: acidity.
Acid in Solution A: 20% of x (in ml)
Acid in Solution B: 50% of y (in ml)
Acid in Mixture: 40% of 90 ml
0.40 x 90ml = 36 ml
Therefore Equation 2 will be:
0.20x + .50y = 36
Solving Word Problems Using Linear
Combinations
Now we must solve the equations using the same steps
we used before:
Equation 1: x + y = 90
Equation 2: 0.2x + 0.50y = 36
Can YOU solve it?
Linear Systems with Infinitely Many
Solutions or None at All
Some Linear Systems are special and have either no
solution OR an infinite number of solutions:
Linear Systems with Infinitely Many
Solutions or None at All
Parallel Lines have NO solution because their lines
NEVER intersect.
Linear Systems with Infinitely Many
Solutions or None at All
Some linear systems have equations that some out to
equal the same line. Because it is the same line, the
two equations are intersecting at every point on their
graphs.
Linear Systems with Infinitely Many
Solutions or None at All
You can prove that a system has infinitely many
solutions or no solution using the same methods to
solve the systems as we used before:
 Graphing
 Substituting
 Linear Combinations
Graphing Systems of Linear Inequalities
A system of linear inequalities is two or more linear
inequalities that use the same variables (i.e. they both
use x and y).
Graphing Systems of Linear Inequalities
A graph of a linear inequality in two
variables is a half-plane. The
boundary line of the half-plane is
dashed if the inequality is < or > and
solid if the inequality is ≤ or ≥.
Graphing Systems of Linear Inequalities
 Example:
x+y<3
x + 4y ≥ 0
Graphing Systems of Linear Inequalities
To graph the system simply put both graphs on the same
paper. The shaded regions will overlap: