* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Pre-Algebra
Survey
Document related concepts
Transcript
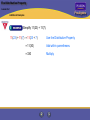
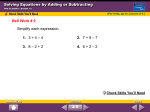
Properties of Numbers Lesson 2-1 Pre-Algebra Objectives: 1. To identify properties of addition and multiplication. 2. To use properties to solve problems. Properties of Numbers Lesson 2-1 Pre-Algebra New Terms: Commutative Properties – changing the order of the values you are adding or multiplying does not change the sum or product. Associative Properties – Changing the grouping of the values you are adding or multiplying does not change the sum or product. Additive Identity – when you add a number to 0, the sum equals the original number. Multiplicative Identity – when you multiply a number to 1, the product equals the original number. Properties of Numbers Lesson 2-1 Additional Examples Carlos spent $42 on his golf game. He then bought a bottle of water for $2 and a chef’s salad for $8. What was the total cost for his golf game and meal? You can use the Associative Property of Addition to find the total cost in two different ways. 42 + (2 + 8) = 42 + 10 = 52 Add 2 and 8 first. (42 + 2) + 8 = 44 + 8 = 52 Add 42 and 2 first. Carlos’s total cost was $52. Pre-Algebra Properties of Numbers Lesson 2-1 Additional Examples Name each property shown. a. 17 + x + 3 = 17 + 3 + x Commutative Property of Addition b. (36 2)10 = 36(2 10) Associative Property of Multiplication c. km = km • 1 Identity Property of Multiplication d. (103 + 26) + 4 = 103 + (26 + 4) Associative Property of Addition Pre-Algebra Properties of Numbers Lesson 2-1 Pre-Algebra Additional Examples Use mental math to simplify (48 + 7) + 2. (48 + 7) + 2 = (7 + 48) + 2 Use the Commutative Property of Addition. = 7 + (48 + 2) Use the Associative Property of Addition. = 7 + 50 Add within parentheses. = 57 Add. Properties of Numbers Lesson 2-1 Pre-Algebra Additional Examples Suppose you buy school supplies costing $.45, $.65, and $1.55. Use mental math to find the cost of these supplies. 0.45 + 0.65 + 1.55 = 0.65 + 0.45 + 1.55 Use the Commutative Property of Addition. = 0.65 + (0.45 + 1.55) Use the Associative Property of Addition. = 0.65 + 2.00 Add within parentheses. = 2.65 Add. The cost of the school supplies is $2.65. Properties of Numbers Lesson 2-1 Pre-Algebra Additional Examples Use mental math to simplify (20 • 13) • 5. (20 • 13) • 5 = (13 • 20) • 5 Use the Commutative Property of Multiplication. = 13 • (20 • 5) Use the Associative Property of Multiplication. = 13 • 100 Multiply within parentheses. = 1,300 Multiply. The Distributive Property Lesson 2-2 Pre-Algebra Objectives: 1. To use the Distributive Property with numerical expressions 2. To use the Distributive Property with algebraic expressions The Distributive Property Lesson 2-2 Pre-Algebra New Terms: Distributive Property – to multiply a sum or difference, multiply each number within the parentheses by the number outside the parantheses. Tips: remember when multiplying by a negative number, the rules for integers still apply. The Distributive Property Lesson 2-2 Pre-Algebra Additional Examples Use the Distributive Property to find 15(110) mentally. 15(110) = 15(100 + 10) Write 110 as (100 + 10). = 15 • 100 + 15 • 10 Use the Distributive Property. = 1,500 + 150 Multiply. = 1,650 Add. The Distributive Property Lesson 2-2 Pre-Algebra Additional Examples Ms. Thomas gave 5 pencils to each of her 37 students. What is the total number of pencils she gave to the students? (37)5 = (40 – 3)5 Write 37 as (40 – 3). = 40 • 5 – 3 • 5 Use the Distributive Property. = 200 – 15 Multiply. = 185 Subtract. Ms. Thomas gave the students 185 pencils. The Distributive Property Lesson 2-2 Pre-Algebra Additional Examples Simplify 11(23) + 11(7). 11(23) + 11(7) = 11(23 + 7) Use the Distributive Property. = 11(30) Add within parentheses. = 330 Multiply. The Distributive Property Lesson 2-2 Pre-Algebra Additional Examples Multiply. a. –9(2 – 8y) –9(2 – 8y) = –9(2) – (–9)(8y) Use the Distributive Property. = –18 – (–72y) Multiply. = –18 + 72y Simplify. b. (5m + 6)11 (5m + 6)11 = (5m)11 + (6)11 Use the Distributive Property. = 55m + 66 Multiply. Simplifying Variable Expressions Lesson 2-3 Pre-Algebra Objectives: 1. To identify parts of a variable expression 2. To simplify expressions Simplifying Variable Expressions Lesson 2-3 Pre-Algebra New Terms: Term – a number or the product of a number and variable(s) Constant – a term that has no variable Like Terms – terms that have identical variables Coefficient – a number that multiples a variable Deductive Reasoning – the process of reasoning logically from given facts to a conclusion. As you use properties, rules, and definitions to justify the steps in a problem, you are using deductive reasoning. Tips: some variable terms have an unwritten coefficient of 1, important to remember when adding like terms. Simplifying Variable Expressions Lesson 2-3 Pre-Algebra Additional Examples Name the coefficients, the like terms, and the constants in 7x + y – 2x – 7. Coefficients: 7, 1, –2 Like terms: 7x, –2x Constant: –7 Simplifying Variable Expressions Lesson 2-3 Pre-Algebra Additional Examples Simplify 2b + b – 4. 2b + b – 4 = 2b + 1b – 4 Use the Identity Property of Multiplication. = (2 + 1)b – 4 Use the Distributive Property. = 3b – 4 Simplify. Simplifying Variable Expressions Lesson 2-3 Pre-Algebra Additional Examples Simplify (7 – 3x)5 + 20x. (7 – 3x)5 + 20x = 35 – 15x + 20x Use the Distributive Property. = 35 + (–15x + 20x) Use the Associative Property of Addition. = 35 + (–15 + 20)x Use the Distributive Property to combine like terms. = 35 + 5x Simplify. Variables and Equations Lesson 2-4 Pre-Algebra Objectives: 1. To classify types of equations. 2. To check equations using substitution Variables and Equations Lesson 2-4 Pre-Algebra New Terms: Equation – is a mathematical sentence with an equal sign Open Sentence – an equation with one or more variables Solution to an Equation – a value to a variable that make the equation “true” Tips: ≠ means not equal The verb “is” indicates an equal sign Variables and Equations Lesson 2-4 Additional Examples State whether each equation is true, false, or an open sentence. Explain. a. 3(b – 8) = 12 open sentence, because there is a variable b. 7 – (–6) = 1 false, because 13 =/ 1 c. –9 + 5 = – 4 true, because – 4 = – 4 Pre-Algebra Variables and Equations Lesson 2-4 Pre-Algebra Additional Examples Write an equation for Six times a number added to the number is the opposite of forty-two. State whether the equation is true, false, or an open sentence. Explain. Words Equation six times the number added to the number 6x added to x is –42 6x + x = –42 is the opposite of forty-two The equation is an open sentence, because there is a variable. Variables and Equations Lesson 2-4 Pre-Algebra Additional Examples Is 45 a solution of the equation 120 + x = 75? 120 + x = 75 120 + 450 75 Substitute 45 for x. 165 =/ 75 No, 45 is not a solution of the equation. Variables and Equations Lesson 2-4 Pre-Algebra Additional Examples A gift pack must hold 20 lb of food. Apples weigh 9 lb and cheese weighs 5 lb. Can the jar of jam that completes the package weigh 7 lb? Words weight of apples Let Equation j plus weight of weight of plus cheese jam 20 lb = 20 = weight of jam. 9 + 5 + 9 + 5 + j = 20 14 + j = 20 Add. 14 + 7 Substitute 7 for the variable. 20 is 21 =/ 20 No, the jar of jam cannot weigh 7 lb. j Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Objectives: 1. To solve one-step equations using subtraction 2. To solve one-step equations using addition Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra New Terms: Inverse Operations – used to get the variable alone Tips: The goal to solving any equation is to “isolate” the variable using inverse operations. You should always simplify both sides of an equation before isolating the variable. Remember to add or subtract BOTH sides by the same number Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Additional Examples Solve y + 5 = 13. Method 1: y + 5 = 13 y + 5 – 5 = 13 – 5 y=8 Method 2: Subtract 5 from each side. Simplify. Check: y + 5 = 13 8 + 5 13 13 = 13 Replace y with 8. y + 5 = 13 –5=–5 y= 8 Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Additional Examples Larissa wants to increase the number of books in her collection to 327 books. She has 250 books now. Find the number of books she needs to buy. Words target number Let Equation x 327 is 250 plus number to buy = number to buy. = 250 + x Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Additional Examples (continued) 327 = 250 + x 327 = x + 250 327 – 250 = x + 250 – 250 77 = x Use the Commutative Property of Addition. Subtract 250 from each side. Simplify. Larissa needs to buy 77 more books. Check: Is the answer reasonable? 250 plus the number of books bought should be a total collection of 327. 250 + 77 = 327 Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Additional Examples Solve c – 23 = – 40. c – 23 = – 40 c – 23 + 23 = – 40 + 23 c = –17 Add 23 to each side. Simplify. Solving Equations by Adding or Subtracting Lesson 2-5 Pre-Algebra Additional Examples Marcy’s CD player cost $115 less than her DVD player. Her CD player cost $78. How much did her DVD player cost? Words cost of CD player Let t Equation was $115 less than cost of DVD player = cost of the DVD player. 78 78 = t – 115 78 + 115 = t – 115 + 115 193 = t Marcy’s DVD player cost $193. = t – Write an equation. Add 115 to each side. Simplify. 115 Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Objectives: 1. To solve one-step equations using division 2. To solve one-step equations using multiplication Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Tips: The division property of equality suggests you can divide each side of an equation by the same nonzero number. Divisors are restricted to nonzero values because division by zero is undefined. Remember to multiply or divide BOTH sides by the same number. Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Additional Examples 288 pens are boxed by the dozen. How many boxes are needed? Words number of pens Let Equation b 288 is 12 times number of boxes • b = number of boxes. = 12 Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Additional Examples (continued) 288 = 12b 288 12b = 12 12 24 = b Divide each side by 12. Simplify. 24 boxes are needed. Check: Is the answer reasonable? Twelve times the number of boxes is the number of pens. Since 12 24 = 288, the answer is reasonable. Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Additional Examples Solve –2v = –24. –2v = –24 –2v –24 = –2 –2 v = 12 Check: Divide each side by –2. Simplify. –2v = –24 –2 • (12) –24 –24 = –24 Replace v with 12. Solving Equations by Multiplying or Dividing Lesson 2-6 Pre-Algebra Additional Examples Solve x = – 5. 8 x 8 =–5 8 x = 8(–5) Multiply each side by 8. 8 x = – 40 Simplify. Problem Solving Strategy: Guess, Check, Revise Lesson 2-7 Pre-Algebra Objectives: 1.To solve a problem using the Guess, Check, Revise strategy Problem Solving Strategy: Guess, Check, Revise Lesson 2-7 Additional Examples Pre-Algebra During the intermission of the play, the Theater Club sold cups of popcorn and soda. The club sold 79 cups of popcorn and 96 sodas for a total of $271. What was the selling price of a cup of popcorn? Of a soda? You can organize conjectures in a table. As a first conjecture, try both with a price of $1. Problem Solving Strategy: Guess, Check, Revise Lesson 2-7 Pre-Algebra Additional Examples (continued) Popcorn Soda Price Price Total Price $1 $1 79(1) + 96(1) = 79 + 96 = 175 The total is too low. Increase the price of the popcorn only. $2 $1 79(2) + 96(1) = 158 + 96 = 254 The total is too low. Increase the price of the soda. $2 $2 79(2) + 96(2) = 158 + 192 The total is too high. = 350 Decrease the price of the popcorn. $1 $2 79(1) + 96(2) = 79 + 192 = 271 The total is correct. The popcorn price was $1, and the soda price was $2. Inequalities and Their Graphs Lesson 2-8 Pre-Algebra Objectives: 1. To graph inequalities 2. To write inequalities Inequalities and Their Graphs Lesson 2-8 Pre-Algebra New Terms: Inequality – a mathematical sentence that contains <,>,≤,≥, or ≠. Solution to an Inequality – any number that makes the inequality true. Tips: Know what the different signs mean, and we do not have gators or crocodiles in this class When reading the solution to an inequality, you should always start with the varible Inequalities and Their Graphs Lesson 2-8 Additional Examples Graph the solutions of each inequality on a number line. a. x > –2 An open dot shows that –2 is not a solution. Shade all the points to the right of –2. b. w > – –5 A closed dot shows that –5 is a solution. Shade all the points to the right of –5. Pre-Algebra Inequalities and Their Graphs Lesson 2-8 Additional Examples (continued) c. k < –4 A closed dot shows that 4 is a solution. Shade all the points to the left of 4. d. y < 6 An open dot shows that 6 is not a solution. Shade all the points to the left of 6. Pre-Algebra Inequalities and Their Graphs Lesson 2-8 Additional Examples Write the inequality shown in each graph. a. x > – –3 b. x<3 Pre-Algebra Inequalities and Their Graphs Lesson 2-8 Pre-Algebra Additional Examples Food can be labeled very low sodium only if it meets the requirement established by the federal government. Use the table to write an inequality for this requirement. Label Definition Sodium-free food Less than 5 mg per serving Very low sodium food At most 35 mg per serving Low-sodium food At most 140 mg per serving Inequalities and Their Graphs Lesson 2-8 Pre-Algebra Additional Examples (continued) Words a serving of very low sodium food Let Inequality v = v has at most 35 mg sodium number of milligrams of sodium in a serving of very low sodium food. < – 35 Solving One-Step Inequalities by Adding or Subtracting Lesson 2-9 Pre-Algebra Objectives: 1. To solve one-step inequalities using subtraction 2. To solve one-step inequalities using addition Solving One-Step Inequalities by Adding or Subtracting Lesson 2-9 Pre-Algebra Tips: Just like the equality properties, you must add or subtract the same number from each side When rewriting an inequality in reverse order, you must pay attention to the direction of the inequality symbol Solving One-Step Inequalities by Adding or Subtracting Lesson 2-9 Pre-Algebra Additional Examples Solve each inequality. Graph the solutions. a. 4 + s < 12 4 + s < 12 4 + s – 4 < 12 – 4 s<8 b. Subtract 4 from each side. Simplify. –16 > – y – 14 –16 > – y – 14 –16 + 14 > – y – 14 + 14 –2 > – y or y < – –2 Add 14 to each side. Simplify. Solving One-Step Inequalities by Adding or Subtracting Lesson 2-9 Pre-Algebra Additional Examples Suppose your computer’s hard drive has a capacity of 6 gigabytes (GB). The files you have stored on the hard drive occupy at least 2 GB. How much storage space is left for other files? storage space for our files plus Words Let s Inequality 2 storage space left total space < – 6 = storage space available. + s 2+s< –6 2–2+s< –6–2 is less than or equal to Subtract 2 from each side. s< Simplify. – 4 At most 4 GB are left. Solving One-Step Inequalities by Adding or Subtracting Lesson 2-9 Pre-Algebra Additional Examples Solve –10 < –13 + q. –10 < –13 + q –10 + 13 < –13 + 13 + q 3<q Add 13 to each side. Simplify. Solving One-Step Inequalities by Multiplying or Dividing Lesson 2-10 Pre-Algebra Objectives: 1. To solve one-step inequalities using division 2. To solve one-step inequalities using multiplication Solving One-Step Inequalities by Multiplying or Dividing Lesson 2-10 Pre-Algebra Tips: When you multiply or divide each side of an inequality by a negative number, you must reverse the direction of the inequality symbol. Solving One-Step Inequalities by Multiplying or Dividing Lesson 2-10 Pre-Algebra Additional Examples A 1-ton truck has the ability to haul 1 ton, or 2,000 lb. At most, how many television sets can the truck carry if each TV set weighs 225 lb? Words is less than number of times 225 lb 2,000 lb or equal to televisions Let x = number of televisions. Inequality 225x < – 2,000 x • 225 < – 2,000 Solving One-Step Inequalities by Multiplying or Dividing Lesson 2-10 Pre-Algebra Additional Examples (continued) 225x < 2,000 225 – 225 x< – 8.8 Divide each side by 225. Simplify. Round the answer down to find a whole number of television sets. At most, the truck can carry 8 television sets. Check: Is the answer reasonable? The total weight of 8 television sets is 8(225) = 1,800 lb, which is less than 2,000 lb but so close that another television set could not be carried. The answer is reasonable. Solving One-Step Inequalities by Multiplying or Dividing Lesson 2-10 Pre-Algebra Additional Examples Solve z < –2. –8 – z < –2 –8 – z –8 –8 > – –8(–2) z> – 16 Multiply each side by –8 and reverse the inequality symbol. Simplify.