Download Solving A Linear System By Substitution

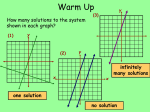
"A true friend is someone who thinks you are a good egg
even though he knows you are slightly cracked.”
Warm Up
How many solutions to the system
shown in each graph?
(1)
y
(3)
y
x
(2)
x
y
x
infinitely
many solutions
one solution
no solution
5-2A Solving Linear Systems by
Substitution
Algebra 1
Glencoe McGraw-Hill
Linda Stamper
Two or more linear equations in the same variable form a
system of linear equations, or simply a linear system.
x+y=5
2x – 3y = 3
Equation 1
Equation 2
A solution of a linear system in two variables is an ordered
pair that makes each equation a true statement.
In the previous lesson you solved a linear system by using a
graph.
The point where the graphs of each equation intersect is
the ordered pair solution. y
x
Point of
intersection
(–1,–3)
•
There are several ways to solve a linear system without
using a graph. In this lesson you will study an algebraic
method known as the substitution method.
Solving A Linear System By Substitution
1) Choose one of the equations and isolate one of the
variables.
2) Substitute the expression from Step 1 into the other
equation and solve.
3) Substitute the solved variable from Step 2 into either
of the original equations and solve. Write the answer as
an ordered pair.
4) Check the ordered pair solution in each of the original
equations.
Here is a linear system:  x  y  1
2x  3y  2
y  x 1
First choose one equation and isolate one of the variables.
You will get the same solution whether you solve for x first
or y first.
You should begin by solving for the variable that is easier
to isolate.
Which of the above equations would be easier to isolate one
of the variables?
Which equation would you choose to isolate the variable?
Name the variable you would solve for first.
3x  y   9
and
2x  4 y  8
and
x  3y  11
solve for y
2x  5 y  33
solve for x
x  2y  10
and
x  3y  0
solve for x in either equation
Solving A Linear System By Substitution
1) Choose one of the equations and isolate one of the
variables.
2) Substitute the expression from Step 1 into the other
equation and solve.
3) Substitute the solved variable from Step 2 into either
of the original equations and solve. Write the answer as
an ordered pair.
4) Check the ordered pair solution in each of the original
equations.
Solve the linear system using the substitution method.
Choose one equation and
xy 1
and
2x  y  2
isolate one of the variables.
y  x  1 2x  (
)  2
Substitute the expression
2x  x  1  2
into the other equation
3x  1  2
and solve.
3x  3
Substitute the solved value
x  1
into one of the original
   y  1
equations and solve.
1 y 1
y0
Write the answer as an ordered pair.
Remember to place the x value first.
(–1,0)
Watch one more time on how to do this problem!
Solve the linear system using the substitution method.
xy 1
and
2x  y  2
y  x  1 2x  (
)  2
2x  x  1  2
3x  1  2
3x  3
x  1
   y  1
1 y 1
y0
(–1,0)
Solve the linear system using substitution.
Example 1 x  4 y  1 and
2 x  2y  3
Example 2 x  2y  0
and 2x  6y  15
Example 3 3x  y  5
and
2x  y  10
Example 1 Solve the linear system.
x  4 yy  11 and
x  4y  1
1

x  4   1
2
x  2  1
x 1
2
2 x  2y  3
  2y  3
8y  2  2y  3
10 y  2  3
10 y  5
1
y
2
 1, 1 
 2


Example 2 Solve the linear system.
x  2y  0 and 2x  6y  15
x  2y
  6y  15
2
4 y  6y  15
10 y  15
15
3
y
10
x  2   0
2
3
y
x 3  0
2
x 3
 3, 3 
 2


Example 3 Solve the linear system.
5 and
33xx  yy  5
2x  y  10
  10
y  3x  5 2x  
2x  3x  5  10
5x  5  10
5x  15
33  y  5
x 3
Did you
9y 5
distribute
the negative y  4
correctly?
(3,–4)
Solve the linear system.
 3x  y  7
 3x
 3x
y  3x  7
and
 6x  2y  8
 6x  2
  8
 6x  23x  7   8
 6x  6x  14  8
14  8
No solution
Write in your notes: When solving produces
a false statement, there is no solution.
What would the graph of this system
look like to show “no solution”?
Parallel lines
y
x
Solve the linear system.
 x  2y  2
and
3x  6y  6
 2y  2y
  6y  6
3
 x  2y  2
6y  6  6y  6
1 1 1
6
6
2
y

2
x  2y 
00
Infinitely many solutions
Write in your notes: When solving produces a true
statement, there are infinitely many solutions.
What would the graph of this system look
like to show “infinitely many solutions”?
Same lines
x
y
Practice Problems. Use substitution to solve each system
of equations. If the system does not have exactly one
solution, state whether it has no solution or infinitely many
solutions. If the system has one solution, name it.
1. 2x  y  5
2x  y  1
no solution
4. x  2y  4
 x  2y  4
Infinitely many
solutions
2.  2x  y  3
3. 2x  y  4
 4x  2y  6
4x  2y  0
Infinitely many
(1,2)
solutions
5. x  y  3
x  2y  4
(2,1)
6. x  3y  4
2x  6y  4
no solution
5-A3 Pages 263-265 #8–19,43–48.